Abstrak
Fungsi khas dari proses titik Poisson adalah proses binomial negatif yang kenaikannya tidak independen tetapi independen tergantung pada variabel gamma yang mendasarinya. Dengan menggunakan representasi proses titik baru untuk proses binomial negatif, kami menggeneralisasi distribusi Poisson–Kingman dan ukuran probabilitas diskrit acak yang sesuai. Keluarga baru yang diusulkan dari ukuran probabilitas acak diskrit ini, yang didefinisikan dengan menormalkan titik-titik proses binomial negatif, menyediakan serangkaian prior baru yang berguna untuk model nonparametrik Bayesian dengan fleksibilitas lebih dari ukuran probabilitas diskrit acak yang diperoleh dengan menormalkan titik-titik proses titik Poisson. Kami mengilustrasikan bagaimana keluarga ukuran probabilitas diskrit acak ini berisi prior Bayesian nonparametrik seperti proses Dirichlet, positif yang dinormalisasimathematical equation-proses stabil, proses Poisson–Dirichlet (PDP), dan lain-lain. Dengan pengukuran gamma Lévy yang sama, kami memperoleh perluasan dari proses Dirichlet dan perkiraannya yang hampir pasti. Dengan menggunakan representasi kami untuk proses binomial negatif, kami mengembangkan representasi seri baru untuk PDP. Kami menunjukkan melalui simulasi bagaimana penggunaan prior dari keluarga ini dapat meningkatkan akurasi model hierarkis nonparametrik Bayesian.
1 Pendahuluan
Pertama-tama kita akan mempertimbangkan ukuran acak Poisson (atau proses titik Poisson), karena proses ini berfungsi sebagai dasar dan berhubungan dengan proses-proses lain melalui fungsi-fungsinya. Susunan proses titik umum mengikuti penjelasan dalam Kallenberg ( 1983 ) dan Resnick ( 1987 , Bab 3).mathematical equationmenjadi ruang kompak lokal dengan basis terhitung dan Borel terkaitnyamathematical equation-aljabar. Biarkanmathematical equationmenjadi ruang semua ukuran titik yang didefinisikan padamathematical equationdengan yang terkaitmathematical equation-aljabar. Proses titikmathematical equationpadamathematical equationadalah peta terukur dari ruang probabilitasmathematical equationDiketahui bahwa hukum probabilitas suatu proses ditentukan secara unik oleh fungsi Laplace-nya. Fungsi Laplace dari proses titikmathematical equationadalah




Kita melihat bahwa bobot ukuran probabilitas diskrit acak yang diidentifikasi dalam ekspresi ( 7 ) hanyalah urutan PK yang ditentukan dalam ekspresi ( 8 ). Di sisa artikel, kita akan menggeneralisasi distribusi PK dan ukuran probabilitas diskrit acak yang dihasilkan dengan memanfaatkan representasi proses titik untuk proses binomial negatif (NBP). Representasi proses titik untuk NBP yang kita gunakan di sini sendiri dibangun langsung dari PRM, tidak seperti representasi dalam Ipsen dan Maller ( 2017 ), di mana mereka menggunakan subordinator yang dipangkas.
Sisa artikel ini disusun sebagai berikut. Di Bagian 2 kami memperoleh representasi baru untuk NBP sebagai fungsional dari PRM; kemudian, dengan menormalkan titik-titik dari proses titik ini, kami menggeneralisasi distribusi PK dan ukuran probabilitas diskrit acak yang sesuai. Kami mencatat bahwa kenaikan NBP tidak independen tetapi independen bersyarat pada variabel gamma yang mendasarinya. Sebagai anggota khusus dari keluarga ukuran probabilitas diskrit acak yang baru didefinisikan, perluasan DP dengan perkiraan yang hampir pasti disajikan di Bagian 3. Di Bagian 4 kami memperoleh representasi deret baru untuk PDP, yang didasarkan pada representasi baru kami dari NBP. Menggunakan aturan penghentian, kami memotong representasi deret baru ini untuk mendapatkan perkiraan deret asli. Melalui studi simulasi, kami membandingkan efisiensi perkiraan ini dengan perkiraan lain untuk proses ini yang dijelaskan dalam literatur, khususnya, Al-Labadi dan Zarepour ( 2014 ). Pada Bagian 5 , kami menunjukkan melalui studi simulasi bagaimana keluarga prior baru yang diperkenalkan dalam artikel ini dapat meningkatkan akurasi model hierarkis nonparametrik Bayesian dalam masalah estimasi kepadatan. Pada Bagian 6, kami merangkum kesimpulan kami secara singkat.
2 Proses binomial negatif



3 Proses Dirichlet yang diperluas dan perkiraannya





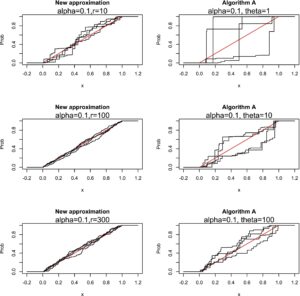

| Baru | Algoritma A | |||
|---|---|---|---|---|
| α | θ | r | d | d |
| 0.1 | 1 | 10 | 0,03133 | 0,35899 |
| 0.1 | 10 | 100 | 0,03819 | 0.19301 |
| 0.1 | 100 | 300 | 0,06443 | 0,13835 |
| 0.5 | 1 | 2 | 0.14497 | 0.24855 |
| 0.5 | 10 | 20 | 0,06549 pukul 0,06549 | 0.14268 |
| 0.5 | 100 | 200 | 0,04606 tahun | 0.10126 |
| 0.9 | 1 | 1 | 0,09294 | 0.18038 |
| 0.9 | 10 | 11 | 0,05178 tahun | 0,10100 |
| 0.9 | 100 | 111 | 0,03998 | 0,07124 tahun |
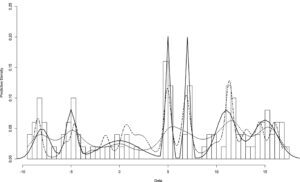
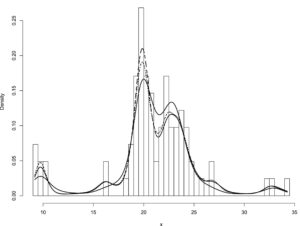
5 Beberapa aplikasi
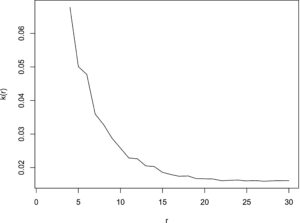
5.1 Mengatur jumlah cluster



| r=3 | r=5 | r=10 | |
|---|---|---|---|
| 0.367597022 | 0.24369485 | 0.16427045 | 0,06353087 |
| 0.168573239 | 0.23947841 | 0.14319002 | 0,05886303 |
| 0.165457071 | 0.10281577 | 0.12842541 | 0,05418117 tahun |
| 0.149080111 | 0.08716432 | 0.10524699 | 0,05112053 |
| 0,058821776 | 0,07639968 | 0,07391248 | 0,04858739 |
| 0,056183134 | 0,05990201 | 0,06339345 | 0,04626107 tahun |
| 0,012551887 | 0,03862790 | 0,05279059 | 0,04349017 |
| 0,007812625 | 0,03184211 | 0,04298598 | 0,03795044 |
| 0,003792634 | 0,02524151 | 0,03705701 | 0,03606621 tahun |
| 0,001971704 | 0,01939928 | 0,03245281 | 0,03021665 |