ABSTRAK
Kami mengusulkan kelas baru regresi linier fungsional parsial multirespons berdimensi tinggi (MR-PFLR) untuk menyelidiki hubungan antara respons skalar dan serangkaian variabel penjelas, yang mencakup tipe fungsional dan skalar. Dalam kerangka kerja ini, baik dimensionalitas respons maupun jumlah kovariat skalar dapat menyimpang hingga tak terhingga. Untuk memperhitungkan korelasi dalam subjek, kami mengembangkan prosedur estimasi kuadrat terkecil tertimbang yang dikenai penalti berdasarkan analisis komponen utama fungsional (FPCA). Dalam pendekatan ini, matriks presisi diestimasi menggunakan kemungkinan yang dikenai penalti, dan koefisien regresi kemudian diestimasi melalui metode kuadrat terkecil tertimbang yang dikenai penalti, dengan matriks presisi berfungsi sebagai bobot. Metode ini memungkinkan estimasi simultan dari koefisien regresi fungsional dan skalar, serta matriks presisi, sambil mengidentifikasi fitur-fitur yang signifikan. Dalam kondisi ringan, kami menetapkan konsistensi, laju konvergensi, dan properti oracle dari estimator yang diusulkan. Studi simulasi menunjukkan kinerja sampel terbatas dari metode estimasi kami. Selain itu, kegunaan praktis model MR-PFLR ditunjukkan melalui penerapannya pada data inisiatif neuroimaging penyakit Alzheimer (ADNI).
1 Pendahuluan
Dengan kemajuan dalam pengumpulan data dan teknologi penyimpanan, data yang kompleks, berdimensi tinggi, dan terstruktur muncul di banyak bidang ilmiah, seperti ekonometrika, genetika, studi biomedis, dan ilmu kesehatan masyarakat. Sebagian besar data ini dapat dikarakterisasikan sebagai data fungsional, yang telah memacu perkembangan pesat bidang baru dalam statistik, analisis data fungsional (FDA). Analisis data fungsional, dengan fleksibilitasnya yang tinggi dan berbagai aplikasinya dalam menangani kurva, gambar, dan bentuk, atau objek yang lebih umum yang diamati pada domain berdimensi lebih tinggi, telah menarik perhatian yang semakin meningkat dalam beberapa dekade terakhir. Regresi fungsional, yang memungkinkan respons atau variabel prediktor, atau keduanya, menjadi fungsi, merupakan alat penting dalam FDA. Berdasarkan jenis variabel yang terlibat, model regresi fungsional dapat diklasifikasikan menjadi tiga kategori besar: regresi skalar-pada-fungsi (respons skalar dan prediktor fungsional) [ 1 – 3 ], regresi fungsi-pada-skalar (respons fungsional dan prediktor skalar) [ 4 , 5 ], dan regresi fungsi-pada-fungsi (respons fungsional dan prediktor fungsional) [ 6 , 7 ]. Banyak metode telah dikembangkan untuk mempelajari model regresi fungsional ini [ 8 – 14 ].
Yang menjadi perhatian khusus dalam FDA adalah regresi linier fungsional (FLR), yang menangkap hubungan linier antara variabel fungsional dan skalar. Salah satu jenis FLR konvensional dirancang untuk memodelkan hubungan antara respons skalar univariat yang diminati dan satu prediktor fungsional, dengan metode dan teori inferensi statistik yang dikembangkan dengan baik [ 2 , 3 , 15 – 19 ]. Di sisi lain, dalam banyak eksperimen praktis, data yang dikumpulkan pada variabel penjelas tidak hanya mencakup satu prediktor fungsional tetapi kumpulan data tipe campuran yang berisi variabel fungsional dan non-fungsional. Untuk mengatasi aplikasi ini, Shi [ 20 ] mengusulkan model regresi linier fungsional parsial (PFLR) untuk mengkarakterisasi hubungan antara respons skalar dan prediktor tipe campuran, menyajikan estimator untuk koefisien regresi fungsional dan non-fungsional berdasarkan metode analisis komponen utama fungsional (FPCA). Selanjutnya, banyak metode dan teori lanjutan untuk PFLR telah dikembangkan, termasuk metode pemilihan variabel [ 10 , 21 ], regresi kuantil [ 22 – 25 ], pendekatan estimasi kuat [ 26 , 27 ], dan uji hipotesis serta inferensi [ 28 , 29 ], di antara banyak lainnya.
Karena kemampuannya untuk menangani data tipe campuran dan kompleks, model PFLR telah diterapkan secara luas dalam studi pencitraan biologis dan medis. Misalnya, dalam studi genetik pencitraan, seperti studi inisiatif neuroimaging penyakit Alzheimer (ADNI) [ 30 ], sering kali diinginkan untuk mengaitkan ekspresi gen, data pencitraan, dan karakteristik individu dengan penilaian klinis seperti kognisi, stadium penyakit, skor gangguan, dan status perkembangan untuk mengeksplorasi jalur biologis fenotipe terkait penyakit. Suatu jalur dapat melibatkan ribuan gen dan variabel klinis, dengan hanya sebagian kecil yang kemungkinan berkorelasi dengan penyakit Alzheimer (AD). Mengidentifikasi fitur penting yang sangat terkait dengan AD dari ribuan gen sangat penting untuk memahami jalur biologis penyakit tersebut, yang berpotensi memfasilitasi identifikasi risiko penyakit sejak dini.
Pemeriksaan status mental mini (MMSE) adalah kuesioner 30 poin yang umumnya digunakan untuk menilai gangguan kognitif. Ini adalah salah satu alat yang paling banyak digunakan untuk menyaring AD, dengan skor yang lebih rendah menunjukkan tingkat keparahan yang lebih besar. Para peneliti telah menyelidiki berbagai faktor yang memengaruhi AD berdasarkan skor MMSE. Misalnya, Yao et al. [ 22 ] dan Ma et al. [ 23 ] memperlakukan skor MMSE sebagai respons skalar, mengubah pencitraan volume otak menjadi kurva kepadatan probabilitas yang ditransformasikan log sebagai prediktor fungsional, dan menggunakan PFLR untuk mengeksplorasi pengaruh grafik pencitraan otak pada AD. Wang et al. [ 24 ] selanjutnya menyelidiki hubungan antara skor MMSE dan data genetik, pencitraan, dan klinis (GIC) menggunakan model linier fungsional parsial. Li et al. [ 31 ] mengusulkan kerangka kerja pemodelan linier fungsional parsial dengan menanamkan data pencitraan volume otak ke dalam ruang Hilbert kernel yang mereproduksi untuk mengeksplorasi jalur terkait GIC berdimensi tinggi untuk AD.
Meskipun penelitian ekstensif tentang AD menggunakan model regresi linier fungsional parsial (PFLR), sebagian besar penelitian yang ada, sejauh pengetahuan kami, berfokus terutama pada hasil univariat. Namun, dalam banyak aplikasi dunia nyata, respons multivariat yang berkorelasi umumnya diamati, khususnya dalam bidang yang sedang berkembang seperti genomik dan neuroimaging. Bidang-bidang ini sering kali melibatkan data berdimensi tinggi yang terdiri dari sejumlah besar kovariat skalar, prediktor fungsional, dan respons multivariat, yang cenderung berkorelasi dalam setiap subjek.
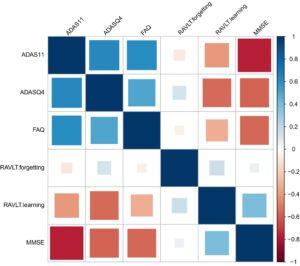
Misalnya, studi pencitraan medis skala besar telah mengembangkan berbagai metode dan algoritma untuk mengukur tingkat keparahan gangguan kognitif untuk AD, yang mengarah ke beberapa tes skrining yang berharga [ 32 , 33 ]. Salah satu tes tersebut adalah Rey Auditory Verbal Learning Test (RAVLT), yang menilai pembelajaran verbal dan memori melalui skor seperti RAVLT.learning (kemampuan belajar) dan RAVLT.forgetting (tingkat lupa). Pengukuran lain, Functional Assessment Questionnaire (FAQ), adalah kuesioner berbasis informan yang diberikan oleh dokter yang mengevaluasi gangguan fungsional kehidupan sehari-hari pada demensia. Subskala Kognitif dari skala penilaian penyakit Alzheimer (ADAS) terdiri dari 11 tugas, termasuk tes yang diselesaikan subjek dan penilaian berbasis pengamat, yang mencakup domain memori, bahasa, dan praksis. Total skor ADAS (ADAS11) berkisar dari 0 hingga 70, berdasarkan jumlah skor tugas individu. Selain itu, studi ADNI menyertakan skor dari Tugas 4 (Pengenalan Kata, ADASQ4).
Gambar 1 mengilustrasikan korelasi di antara skor kognitif ini. Khususnya, MMSE dan RAVLT.learning menunjukkan korelasi positif, di mana nilai yang lebih rendah menunjukkan gangguan kognitif yang lebih parah. Sebaliknya, FAQ, ADAS11, dan ADASQ4 berkorelasi negatif, dengan nilai yang lebih tinggi mencerminkan gangguan yang lebih parah. Lebih jauh, korelasi antara RAVLT.forgetting dan variabel lainnya lemah, yang menunjukkan struktur yang jarang dalam matriks korelasi variabel-variabel ini.
Hal ini memotivasi kami untuk mengembangkan kelas PFLR baru dengan adanya respons multivariat, yang kami sebut sebagai regresi linier fungsional parsial multirespons berdimensi tinggi (MR-PFLR). Model MR-PFLR bertujuan untuk menangkap hubungan antara respons multivariat dan kovariat tipe campuran berdimensi tinggi. Model ini akan mengakomodasi situasi di mana dimensi respons dan kovariat skalar besar, sekaligus memperhitungkan korelasi dalam subjek. Dalam artikel ini, kami fokus pada estimasi dan pemilihan variabel untuk model MR-PFLR yang diusulkan.

Untuk mengatasi tantangan ini dan memperhitungkan korelasi dalam subjek, yang sangat penting untuk meningkatkan akurasi prediksi dalam analisis multivariat [ 34 ], kami mengusulkan prosedur estimasi kuadrat terkecil tertimbang terhukum (FPWLS) berbasis FPCA. Metode ini memungkinkan kami untuk mengidentifikasi prediktor fungsional dan skalar yang signifikan dan memperkirakan koefisien regresi yang sesuai secara bersamaan. Secara khusus, pertama-tama kami memperkirakan koefisien regresi fungsional dan skalar menggunakan metode kuadrat terkecil terhukum (FPLS) berbasis FPCA tanpa menggabungkan korelasi di antara respons. Estimator yang dihasilkan kemudian digunakan untuk memperkirakan matriks presisi pada langkah kedua. Selanjutnya, kami memperkirakan matriks presisi menggunakan kemungkinan terhukum dan memperoleh estimator koefisien regresi yang disempurnakan melalui prosedur FPWLS, dengan matriks presisi berfungsi sebagai matriks tertimbang. Prosedur ini secara alami memanfaatkan struktur korelasi dalam subjek dalam data respons multivariat, meningkatkan efisiensi estimator koefisien regresi.
Artikel ini memberikan tiga kontribusi utama. Pertama, kami memperkenalkan kerangka kerja MR-PFLR yang memperluas model PFLR konvensional dari univariat ke respons berdimensi ganda atau bahkan tinggi. Kedua, kami mengembangkan prosedur estimasi FPWLS, yang secara bersamaan melakukan pemilihan variabel dan mengestimasi koefisien regresi. Efektivitas model dan metode estimasi yang diusulkan ditunjukkan melalui studi simulasi dan analisis data nyata AD. Terakhir, kami menetapkan sifat teoritis dari estimator yang dihasilkan, termasuk konsistensi, laju konvergensi, dan sifat oracle, dalam pengaturan asimtotik dua arah yang mengakomodasi divergensi hingga tak terhingga dari jumlah respons atau jumlah kovariat skalar untuk setiap subjek.
Sisa artikel ini disusun sebagai berikut. Di Bagian 2 , kami memperkenalkan kerangka kerja model MR-PFLR. Bagian 3 merinci prosedur estimasi FPWLS. Bagian 4 menetapkan sifat teoritis dari estimator yang diusulkan. Studi simulasi dan analisis data nyata pada studi ADNI disajikan masing-masing di Bagian 5 dan 6. Bagian 7 menyimpulkan artikel ini.
2 Regresi Linier Fungsional Parsial Multirespon
Kami memperkenalkan model MR-PFLR berikut:


3 Estimasi Dua Langkah Berbasis FPCA
Pada bagian ini, kami menyajikan prosedur estimasi dua langkah berbasis FPCA yang diusulkan secara terperinci dan memperkenalkan pendekatan berbasis data untuk memilih parameter penyetelan. Kami mulai dengan merepresentasikan prediktor fungsional menggunakan perluasan basis komponen utama fungsional.


















| Struktur korelasi | ρ | Metode | PSR f | NSR f | PSR s | NSR s | MSE f | MSE s | Bahasa Inggris |
|---|---|---|---|---|---|---|---|---|---|
| AR | 0.4 | FPLS | 1 | 1 | 1 | 0,950 | 0,218 (0,164) | 0,057 (0,034) | 0,088 (0,043) |
| FPLS-Oracle | — | — | — | — | 0,220 (0,164) | 0,049 (0,031) | 0,087 (0,043) | ||
| FPWLS | 1 | 1 | 1 | 0,957 tahun | 0,213 (0,164) | 0,045 (0,027) | 0,085 (0,042) | ||
| FPWLS-Oracle | — | — | — | — | 0,217 (0,175) | 0,040 (0,026) | 0,084 (0,042) | ||
| 0.7 | FPLS | 1 | 1 | 1 | 0,952 | 0,275 (0,236) | 0,053 (0,030) | 0,091 (0,052) | |
| FPLS-Oracle | — | — | — | — | 0,278 (0,235) | 0,047 (0,029) | 0,090 (0,052) | ||
| FPWLS | 1 | 1 | 1 | 0,959 | 0,253 (0,231) | 0,029 (0,018) | 0,081 (0,050) | ||
| FPWLS-Oracle | — | — | — | — | 0,252 (0,231) | 0,025 (0,016) | 0,080 (0,050) | ||
| 0.9 | FPLS | 1 | 1 | 1 | 0,954 | 0,260 (0,207) | 0,057 (0,045) | 0,090 (0,064) | |
| FPLS-Oracle | — | — | — | — | 0,265 (0,217) | 0,049 (0,034) | 0,089 (0,065) | ||
| FPWLS | 1 | 1 | 1 | 0,966 tahun | 0,241 (0,243) | 0,014 (0,010) | 0,076 (0,063) | ||
| FPWLS-Oracle | — | — | — | — | 0,246 (0,256) | 0,012 (0,009) | 0,076 (0,063) | ||
| MANTAN | 0.4 | FPLS | 1 | 0,999 | 1 | 0,949 tahun | 0,243 (0,191) | 0,060 (0,032) | 0,089 (0,039) |
| FPLS-Oracle | — | — | — | — | 0,236 (0,183) | 0,054 (0,031) | 0,087 (0,040) | ||
| FPWLS | 1 | 1 | 1 | 0,953 | 0,219 (0,177) | 0,042 (0,021) | 0,082 (0,038) | ||
| FPWLS-Oracle | — | — | — | — | 0,220 (0,178) | 0,036 (0,020) | 0,081 (0,038) | ||
| 0.7 | FPLS | 1 | 1 | 1 | 0,945 tahun | 0,293 (0,264) | 0,057 (0,037) | 0,092 (0,058) | |
| FPLS-Oracle | — | — | — | — | 0,297 (0,262) | 0,049 (0,031) | 0,091 (0,058) | ||
| FPWLS | 1 | 1 | 1 | 0,957 tahun | 0,270 (0,269) | 0,027 (0,016) | 0,080 (0,058) | ||
| FPWLS-Oracle | — | — | — | — | 0,271 (0,270) | 0,022 (0,013) | 0,078 (0,058) | ||
| 0.9 | FPLS | 1 | 1 | 1 | 0,950 | 0,258 (0,237) | 0,059 (0,043) | 0,097 (0,064) | |
| FPLS-Oracle | — | — | — | — | 0,258 (0,234) | 0,055 (0,036) | 0,096 (0,063) | ||
| FPWLS | 1 | 1 | 1 | 0,961 tahun | 0,232 (0,250) | 0,013 (0,012) | 0,082 (0,060) | ||
| FPWLS-Oracle | — | — | — | — | 0,231 (0,253) | 0,010 (0,007) | 0,082 (0,060) |
Catatan: Yang ditampilkan adalah rata-rata Monte Carlo (dengan kesalahan standar dalam tanda kurung) dari rasio seleksi positif (PSR), rasio seleksi negatif (NSR), dan kesalahan kuadrat rata-rata (MSE) untuk koefisien fungsional dan skalar, beserta kesalahan prediksi (PE).
| Struktur korelasi | ρ | Metode | PSR f | NSR f | PSR s | NSR s | MSE f | MSE s | Bahasa Inggris |
|---|---|---|---|---|---|---|---|---|---|
| AR | 0.4 | FPLS | 1 | 1 | 1 | 0,953 | 0,126 (0,063) | 0,036 (0,021) | 0,075 (0,036) |
| FPLS-Oracle | — | — | — | — | 0,126 (0,063) | 0,032 (0,019) | 0,074 (0,036) | ||
| FPWLS | 1 | 1 | 1 | 0,956 | 0,121 (0,060) | 0,029 (0,016) | 0,072 (0,035) | ||
| FPWLS-Oracle | — | — | — | — | 0,121 (0,060) | 0,025 (0,016) | 0,072 (0,035) | ||
| 0.7 | FPLS | 1 | 1 | 1 | 0,960 | 0,129 (0,061) | 0,035 (0,022) | 0,075 (0,046) | |
| FPLS-Oracle | — | — | — | — | 0,129 (0,061) | 0,032 (0,020) | 0,074 (0,046) | ||
| FPWLS | 1 | 1 | 1 | 0,961 tahun | 0,110 (0,051) | 0,019 (0,012) | 0,068 (0,046) | ||
| FPWLS-Oracle | — | — | — | — | 0,110 (0,051) | 0,016 (0,010) | 0,068 (0,046) | ||
| 0.9 | FPLS | 1 | 1 | 1 | 0.962 | 0,136 (0,083) | 0,035 (0,029) | 0,076 (0,060) | |
| FPLS-Oracle | — | — | — | — | 0,136 (0,083) | 0,032 (0,026) | 0,075 (0,060) | ||
| FPWLS | 1 | 1 | 1 | 0,967 tahun | 0,099 (0,071) | 0,008 (0,007) | 0,063 (0,058) | ||
| FPWLS-Oracle | — | — | — | — | 0,100 (0,071) | 0,007 (0,004) | 0,063 (0,058) | ||
| MANTAN | 0.4 | FPLS | 1 | 1 | 1 | 0,957 tahun | 0,125 (0,050) | 0,035 (0,020) | 0,075 (0,041) |
| FPLS-Oracle | — | — | — | — | 0,125 (0,050) | 0,032 (0,018) | 0,074 (0,041) | ||
| FPWLS | 1 | 1 | 1 | 0,958 | 0,117 (0,066) | 0,027 (0,014) | 0,070 (0,041) | ||
| FPWLS-Oracle | — | — | — | — | 0,114 (0,048) | 0,023 (0,013) | 0,069 (0,040) | ||
| 0.7 | FPLS | 1 | 1 | 1 | 0,956 | 0,130 (0,063) | 0,035 (0,022) | 0,070 (0,052) | |
| FPLS-Oracle | — | — | — | — | 0,130 (0,063) | 0,032 (0,020) | 0,069 (0,052) | ||
| FPWLS | 1 | 1 | 1 | 0,958 | 0,102 (0,058) | 0,017 (0,010) | 0,061 (0,051) | ||
| FPWLS-Oracle | — | — | — | — | 0,102 (0,058) | 0,014 (0,009) | 0,060 (0,051) | ||
| 0.9 | FPLS | 1 | 1 | 1 | 0,950 | 0,147 (0,089) | 0,038 (0,029) | 0,075 (0,063) | |
| FPLS-Oracle | — | — | — | — | 0,150 (0,094) | 0,033 (0,023) | 0,074 (0,063) | ||
| FPWLS | 1 | 1 | 1 | 0,960 | 0,119 (0,131) | 0,007 (0,005) | 0,062 (0,061) | ||
| FPWLS-Oracle | — | — | — | — | 0,119 (0,131) | 0,006 (0,004) | 0,061 (0,061) |
Catatan: Yang ditampilkan adalah rata-rata Monte Carlo (dengan kesalahan standar dalam tanda kurung) dari rasio seleksi positif (PSR), rasio seleksi negatif (NSR), dan kesalahan kuadrat rata-rata (MSE) untuk koefisien fungsional dan skalar, beserta kesalahan prediksi (PE).
| Struktur korelasi | ρ | Metode | PSR f | NSR f | PSR s | NSR s | MSE f | MSE s | Bahasa Inggris |
|---|---|---|---|---|---|---|---|---|---|
| AR | 0.4 | FPLS | 1 | 1 | 1 | 0,963 | 0,100 (0,032) | 0,025 (0,014) | 0,075 (0,035) |
| FPLS-Oracle | — | — | — | — | 0,100 (0,032) | 0,023 (0,014) | 0,075 (0,035) | ||
| FPWLS | 1 | 1 | 1 | 0,968 | 0,096 (0,031) | 0,019 (0,011) | 0,073 (0,035) | ||
| FPWLS-Oracle | — | — | — | — | 0,096 (0,031) | 0,018 (0,011) | 0,073 (0,035) | ||
| 0.7 | FPLS | 1 | 1 | 1 | 0,953 | 0,099 (0,040) | 0,028 (0,018) | 0,074 (0,046) | |
| FPLS-Oracle | — | — | — | — | 0,099 (0,040) | 0,025 (0,015) | 0,073 (0,046) | ||
| FPWLS | 1 | 1 | 1 | 0,963 | 0,083 (0,030) | 0,014 (0,008) | 0,067 (0,045) | ||
| FPWLS-Oracle | — | — | — | — | 0,083 (0,030) | 0,013 (0,008) | 0,067 (0,045) | ||
| 0.9 | FPLS | 1 | 1 | 1 | 0,955 | 0,102 (0,041) | 0,024 (0,018) | 0,072 (0,062) | |
| FPLS-Oracle | — | — | — | — | 0,101 (0,041) | 0,021 (0,016) | 0,071 (0,062) | ||
| FPWLS | 1 | 1 | 1 | 0,972 tahun | 0,072 (0,026) | 0,005 (0,004) | 0,062 (0,061) | ||
| FPWLS-Oracle | — | — | — | — | 0,072 (0,026) | 0,005 (0,004) | 0,062 (0,060) | ||
| MANTAN | 0.4 | FPLS | 1 | 1 | 1 | 0,949 tahun | 0,099 (0,034) | 0,028 (0,018) | 0,065 (0,039) |
| FPLS-Oracle | — | — | — | — | 0,100 (0,035) | 0,024 (0,015) | 0,064 (0,039) | ||
| FPWLS | 1 | 1 | 1 | 0,955 | 0,089 (0,030) | 0,020 (0,013) | 0,061 (0,038) | ||
| FPWLS-Oracle | — | — | — | — | 0,089 (0,030) | 0,018 (0,011) | 0,061 (0,038) | ||
| 0.7 | FPLS | 1 | 1 | 1 | 0,964 tahun | 0,107 (0,045) | 0,025 (0,016) | 0,075 (0,056) | |
| FPLS-Oracle | — | — | — | — | 0,107 (0,045) | 0,023 (0,015) | 0,075 (0,056) | ||
| FPWLS | 1 | 1 | 1 | 0,963 | 0,082 (0,031) | 0,011 (0,007) | 0,067 (0,056) | ||
| FPWLS-Oracle | — | — | — | — | 0,082 (0,031) | 0,009 (0,006) | 0,067 (0,056) | ||
| 0.9 | FPLS | 1 | 1 | 1 | 0,965 | 0,101 (0,044) | 0,025 (0,018) | 0,076 (0,063) | |
| FPLS-Oracle | — | — | — | — | 0,101 (0,044) | 0,023 (0,016) | 0,075 (0,063) | ||
| FPWLS | 1 | 1 | 1 | 0,963 | 0,069 (0,027) | 0,005 (0,003) | 0,066 (0,062) | ||
| FPWLS-Oracle | — | — | — | — | 0,069 (0,027) | 0,004 (0,003) | 0,066 (0,062) |
Catatan: Yang ditampilkan adalah rata-rata Monte Carlo (dengan kesalahan standar dalam tanda kurung) dari rasio seleksi positif (PSR), rasio seleksi negatif (NSR), dan kesalahan kuadrat rata-rata (MSE) untuk koefisien fungsional dan skalar, beserta kesalahan prediksi (PE).
6 Aplikasi
Kami sekarang menerapkan model yang diusulkan ke kumpulan data yang dikumpulkan dalam studi ADNI. Salah satu tujuan utama studi ADNI adalah untuk menguji apakah neuroimaging struktural dan fungsional, bersama dengan penanda genetik, penilaian klinis dan neuropsikologis, dapat diintegrasikan untuk mengukur perkembangan gangguan kognitif ringan (MCI) dan penyakit Alzheimer (AD) awal [ 46 ]. Tujuan kami adalah untuk mengeksplorasi variabel GIC mana dan bagaimana mereka bersama-sama memengaruhi skor MMSE, RAVLT.learning, RAVLT.forgetting, FAQ, ADAS11, dan ADASQ4 secara bersamaan. Ringkasan singkatan skor kognitif ini ditemukan di Tabel S1 dalam Informasi Pendukung . Pendekatan pemodelan yang diusulkan digunakan untuk menganalisis data dengan menanamkan informasi yang relevan di antara variabel kognitif ini ke dalam proses estimasi untuk meningkatkan akurasi. Secara khusus, kami menggunakan fungsi kepadatan probabilitas yang ditransformasikan-log dari pencitraan volume otak dari dua wilayah yang diminati (ROI), termasuk talamus kiri dan ventrikel lateral kanan, sebagai prediktor fungsional (lihat Gambar 5 ). Beberapa indeks klinis, termasuk usia, jenis kelamin (0 = laki-laki; 1 = perempuan), tangan dominan (0 = kanan; 1 = kiri), tahun pendidikan, dan 1071 polimorfisme nukleotida tunggal (SNP) pada 37 gen kandidat AD teratas, digunakan sebagai kovariat skalar. Kami menstandardisasi semua skor kognitif dan kovariat skalar, dan memusatkan prediktor fungsional. Setelah menghilangkan sampel yang tidak dapat digunakan, kami memperoleh 392 sampel pasien yang didiagnosis dengan MCI.

| Metode | Tes MMSE | RAVLT.belajar | RAVLT.melupakan | Tanya Jawab Umum | ADAS11 | ADASQ4 |
|---|---|---|---|---|---|---|
| FPLS | tanggal 21.01 | 20.53 | 20.66 | 23.87 | 22.80 | 22.24 |
| FPWLS | 1.27 | 1.38 | 1.31 | 1.23 | 1.18 | 1.34 |
| Bahasa Indonesia: iFPLS | Jam 32.30 | 30.62 | 4.31 | 1.85 | 44.61 | 3.53 |
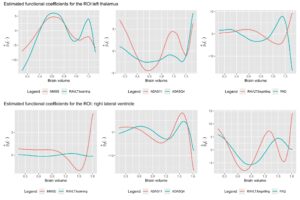
Kami memperkirakan koefisien fungsional untuk ROI: thalamus kiri dan ventrikel lateral kanan menggunakan metode FPWLS yang diusulkan dan menampilkannya dalam tiga kelompok berdasarkan kesamaan tren fungsi kemiringan yang diperkirakan, seperti yang ditunjukkan pada Gambar 6. Pengelompokan ini konsisten dengan korelasi antara skor kognitif. Fungsi kemiringan ROI: thalamus kiri dan ventrikel lateral kanan, masing-masing, dipamerkan di baris pertama dan kedua Gambar 6. Terlihat bahwa kurva kemiringan pada kelompok pertama (MMSE dan RAVLT.learning) menunjukkan kecenderungan yang jelas untuk meningkat, kemudian menurun, kemudian meningkat lagi, dan kemudian menurun lagi saat volume otak meningkat, sedangkan kurva kemiringan pada kelompok kedua (ADAS11 dan ADASQ4) menunjukkan tren yang berlawanan. Fungsi kemiringan pada kelompok ketiga (RAVLT.forgetting dan FAQ) relatif datar ketika volume otak kurang dari 1,0, tetapi menunjukkan tren peningkatan atau penurunan yang signifikan ketika volume otak melebihi 1,0. Fungsi kemiringan ROI: ventrikel lateral kanan menunjukkan tren yang sama sekali berbeda dari ROI: thalamus kiri. Kurva kemiringan ROI: ventrikel lateral kanan pada kelompok pertama dan kedua menunjukkan perilaku yang relatif datar ketika volume otak kurang dari 1,2, dan tren yang relatif jelas ketika volume otak lebih besar dari 1,2. Kurva kemiringan pada kelompok ketiga menunjukkan pasang surut ke bawah dan ke atas dengan meningkatnya volume otak. Temuan ini menunjukkan bahwa daerah otak yang berbeda dengan volume otak yang berbeda memiliki efek yang berbeda pada skor kognitif yang berbeda, dengan pola efek yang sama pada variabel kognitif yang berkorelasi sangat positif.
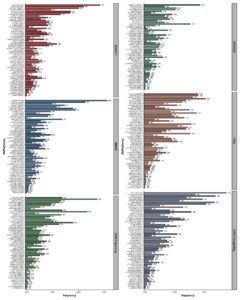
Koefisien regresi kovariat klinis yang diestimasi dengan metode FPWLS disajikan dalam Tabel 6. Dapat diamati bahwa usia dan pendidikan adalah dua variabel klinis dengan dampak signifikan pada AD. Variabel Pendidikan, khususnya, menunjukkan korelasi positif dengan MMSE, RAVLT.learning dan RAVLT.forgetting, dan korelasi negatif dengan ADAS11, ADASQ4 dan FAQ, yang menunjukkan bahwa semakin tinggi tingkat pendidikan, semakin rendah tingkat keparahan AD. Untuk lebih menunjukkan variabel klinis dan SNP mana yang sangat terkait dengan AD, kami menyesuaikan model berdasarkan 500 sampel bootstrap. Variabel yang dipilih dengan frekuensi lebih besar dari 50% dianggap sebagai variabel penting dan efektif dalam proses bootstrap. Tabel 7 menampilkan frekuensi kovariat klinis yang dipilih oleh prosedur FPWLS, yang menunjukkan bahwa keempat kovariat klinis diidentifikasi sebagai variabel signifikan. Gambar 7 menunjukkan frekuensi SNP yang dipilih lebih dari 250 kali di 500 bootstrap. Hasil pada Gambar 7 menunjukkan bahwa gen yang berbeda memiliki mekanisme pengaruh yang berbeda pada variabel kognitif yang berbeda. Khususnya, gen clusterin (CLU), GRB2 associated binding protein 2 (GAB2), sortilin related VPS10 domain containing receptor 1 (SORCS1), thyroid hormone receptor alpha (THRA), membrane spanning 4-domains A6A (MS4A6A), tyrosine kinase non receptor 1 (TNK1), endothelin converting enzyme 1 (ECE1), cholesterol 25-hydroxylase (CH25H), interleukin 33 (IL33), transferrin (TF), CC motif chemokine receptor 2 (CCR2), sortilin related receptor 1 (SORL1), ornithine transcarbamylase (OTC), dan phosphatidylinositol-binding clathrin assembly protein (PICALM) secara signifikan memengaruhi semua skor kognitif.
| kovariat | Tes MMSE | ADAS11 | ADASQ4 | RAVLT.belajar | RAVLT.melupakan | Tanya Jawab Umum |
|---|---|---|---|---|---|---|
| Jenis kelamin | -0,7222 | — | — | -0,0011 | 0,0010 | — |
| Usia | -0,4269 | — | -0,0002 | -0,3129 | -0,2453 | 0.1918 |
| Kepraktisan | 3.8025 | — | 0,0594 tahun | — | — | — |
| Pendidikan | 0.8655 | -0,576 | -1.4154 | 0.1230 | 0,0045 pukul 0,0045 | -0,8238 |
| kovariat | Tes MMSE | ADAS11 | ADASQ4 | RAVLT.belajar | RAVLT.melupakan | Tanya Jawab Umum |
|---|---|---|---|---|---|---|
| Jenis kelamin | 297 | 367 | 309 | 348 | 317 | 316 |
| Usia | 265 | 276 | 266 | 267 | 298 | 283 |
| Kepraktisan | 361 | 264 | 264 | 274 | 269 | 262 |
| Pendidikan | 351 | 296 | 341 | 292 | 285 | 274 |
7 Kesimpulan
Artikel ini mempelajari kelas regresi linier fungsional parsial multirespons yang memungkinkan variabel respons dan kovariat skalar menjadi berdimensi tinggi. Prosedur estimasi kuadrat terkecil tertimbang terhukum berbasis FPCA dikembangkan untuk memperkirakan koefisien regresi dan mengidentifikasi prediktor fungsional dan skalar yang signifikan secara bersamaan. Metode yang diusulkan mengintegrasikan kuadrat terkecil terhukum dan kemungkinan terhukum, meningkatkan efisiensi estimasi dengan menggabungkan korelasi dalam subjek dan memfasilitasi implementasi dengan algoritma yang ada. Kami menetapkan beberapa sifat teoritis mengenai estimator yang dihasilkan, termasuk tingkat konvergensi dan distribusi asimtotik. Studi simulasi dan analisis data ADNI dilakukan untuk menggambarkan keuntungan dari model dan metode estimasi yang diusulkan.