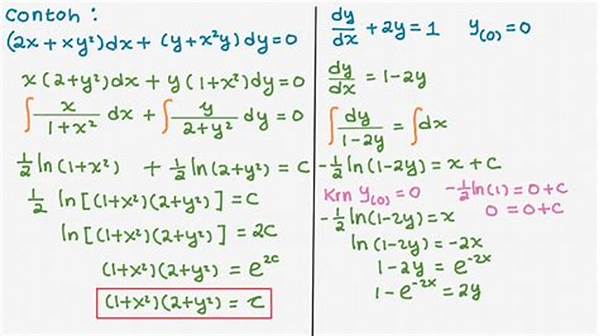Artikel: Persamaan Diferensial

Mengapa Persamaan Diferensial Penting?

Pernahkah Anda merasa seperti ilmuwan jenius ketika memecahkan persamaan matematika kompleks? Jika belum, mungkin Anda belum bertemu dengan persamaan diferensial. Seperti detektif yang mencari petunjuk, persamaan diferensial membantu kita mengurai misteri alam semesta. Dari merancang pesawat luar angkasa hingga memprediksi cuaca, semuanya membutuhkan campur tangan persamaan ini. Bahkan, kehidupan sehari-hari kita tidak bisa lolos dari cengkeraman pengaruh persamaan diferensial. Tak heran jika banyak ilmuwan dan insinyur yang menyebutnya sebagai “senjata rahasia” dalam arsenal matematika mereka. Jadi, sudah siapkah Anda untuk menggali lebih dalam dan menemukan rahasia tersembunyi di balik persamaan diferensial? Tenang saja, artikel ini akan membawa Anda dalam perjalanan yang menyenangkan dan sarat dengan humor tentang anatomi persamaan diferensial.

Paragraf pertama akan membawa kita pada kisah awal persamaan diferensial. Bermula dari kebutuhan manusia untuk memecahkan masalah yang berputar di sekeliling kita — mulai dari arus air yang mengalir melewati sungai hingga kecepatan kendaraan di jalan raya. Pada dasarnya, seluruh dunia bergerak dalam hitungan yang dapat dijelaskan oleh persamaan diferensial. Melalui kekuatan matematika ini, kita dapat membuat perhitungan akurat untuk mengoptimalkan kehidupan sehari-hari.

Masuk ke paragraf kedua, mari kita selami lebih dalam bagaimana persamaan diferensial diterapkan dalam berbagai bidang. Sebut saja dunia medis yang mengandalkannya untuk memproyeksikan pertumbuhan bakteri atau ahli ekologi yang menggunakannya untuk memetakan penyebaran populasi hewan. Bahkan, di dunia pemasaran pun, persamaan ini digunakan untuk menganalisis tren konsumen — ini adalah heroik matematika yang layak mendapatkan perhatian lebih.

Di paragraf ketiga, mari kita lihat testimonial dari para ahli yang telah merasakan keajaiban persamaan diferensial. Banyak peneliti dan profesional berbagi pengalaman mereka dalam menerapkan persamaan ini yang membawa hasil menakjubkan dalam pekerjaan mereka. Seorang insinyur mesin mungkin bercerita tentang bagaimana ia berhasil meningkatkan efisiensi mesin dengan menggunakan persamaan diferensial, atau ahli biologi yang dapat meramalkan pola migrasi burung dengan akurasi tinggi.

Pengantar Persamaan Diferensial untuk Pemula

Paragraf terakhir akan menutup dengan sebuah ajakan untuk bertindak. Tidak ada kata terlambat untuk mulai mempelajari dan memanfaatkan persamaan diferensial. Dengan pengetahuan ini, Anda dapat meningkatkan kemampuan analisis dan problem-solving yang bisa diterapkan pada berbagai sektor. Jika Anda merasa terinspirasi, jangan ragu menghubungi jasa edukasi yang menawarkan kursus persamaan diferensial. Siapa tahu, mungkin Anda adalah detektif matematika berikutnya yang akan membuat terobosan besar!

Perkenalan kepada Keajaiban Persamaan Diferensial

Dalam dunia matematika, kita seringkali dihadapkan dengan berbagai jenis persamaan. Namun, di antara semua jenis tersebut, persamaan diferensial adalah topik yang paling mengintrik dan fenomenal. Persamaan diferensial memungkinkan kita untuk menjawab pertanyaan-pertanyaan besar yang mungkin belum terpikirkan. Apakah kita berbicara tentang bagaimana planet-planet berotasi atau bagaimana virus menyebar dalam populasi, semua ini dapat dimodelkan dengan persamaan diferensial. Bahkan, persamaan ini telah menjadi tulang punggung dari banyak penemuan ilmiah yang inovatif.

Paragraf kedua membahas lebih lanjut mengenai aplikasi praktis dari persamaan diferensial. Dunia teknik, fisika, ekonomi, bahkan biologi, semuanya terhubung erat dengan keilmuan ini. Persamaan diferensial tidak hanya sebagai alat analisis, tetapi juga sebagai metode prediksi yang memungkinkan para ilmuwan memprediksi kecenderungan dan perubahan di masa depan. Misalnya, dalam industri otomotif, persamaan ini diaplikasikan untuk meningkatkan performa aerodinamis kendaraan dengan mengurangi hambatan udara.

Di paragraf ketiga, kita mempelajari lebih mendalam tentang berbagai jenis persamaan diferensial. Terdapat persamaan diferensial biasa dan parsial, masing-masing dengan karakteristik dan penggunaan spesifik. Persamaan diferensial biasa biasanya melibatkan satu variabel tak bebas, sementara persamaan diferensial parsial cenderung lebih kompleks karena melibatkan beberapa variabel tak bebas. Kedua jenis persamaan ini memiliki peranan penting dalam berbagai penelitian yang bertujuan untuk memecahkan masalah dunia nyata.

Akhirnya, paragraf keempat mengajak pembaca untuk mencoba dan mempelajari persamaan diferensial secara langsung. Jangan merasa kecil hati jika menemui kesulitan pada awalnya — ingatlah bahwa para ahli sekalipun memerlukan waktu bertahun-tahun untuk menguasainya. Dengan kesabaran dan latihan, siapa pun dapat menguasai seni persamaan diferensial. Jika Anda tertarik untuk mempelajarinya lebih lanjut, tersedia banyak sumber daya online maupun offline yang menawarkan panduan lengkap dari pemula hingga tingkat lanjut.

Cara Efektif Memahami Persamaan Diferensial

9 Tindakan Mempelajari Persamaan Diferensial

Deskripsi Instruktif: Persamaan Diferensial

Persamaan diferensial adalah cabang ilmu matematika yang berkaitan erat dengan dunia nyata. Tak sekedar teori, persamaan ini menjadi alat penting banyak profesional di berbagai bidang. Dari pengertian sederhananya, persamaan diferensial melibatkan fungsi beserta turunannya. Fungsi tersebut menggambarkan perubahan yang terjadi dalam suatu sistem, baik yang bersifat fisik maupun abstrak. Dengan kata lain, persamaan diferensial adalah matematika dinamis yang mengisahkan perjalanan suatu titik dari keadaan satu ke keadaan lainnya.

Secara detail, persamaan diferensial digunakan untuk memodelkan hubungan antar variabel yang bervariasi terhadap waktu atau ruang. Misalnya, dalam fisika, hukum gerakan Newton bisa dicontohkan dengan persamaan diferensial. Di dunia biologi, kita dapat menemukan aplikasi persamaan ini dalam memprediksi penyebaran penyakit dalam populasi. Dari sinilah kita belajar bahwa persamaan diferensial bukan sekadar bagian dari matematika, tetapi merupakan elemen esensial yang menyingkap misteri bagaimana alam bekerja.

Dengan memahami dan menguasai persamaan diferensial, kita bisa lebih mudah beradaptasi dan menemukan solusi dalam menghadapi tantangan sains dan teknologi masa depan. Persamaan diferensial menjadi panduan bagi kita untuk melakukan terobosan baru dalam penelitian dan pengembangan yang dapat berkontribusi signifikan terhadap kemajuan ilmu pengetahuan. Setiap individu memiliki kesempatan emas untuk mengeksplorasi potensi diri dalam mempelajari persamaan diferensial sebagai bagian dari pembelajaran seumur hidup.

Ilustrasi Inovatif: Persamaan Diferensial dalam Homeschooling

Namun, tidak semua persoalan memiliki jawaban yang mudah. Persamaan diferensial mungkin terlihat mengintimidasi pada pandangan pertama dengan simbol-simbol dan lambang yang membingungkan. Namun, seperti halnya belajar memasak atau berkebun, semakin kita mempraktikannya, semakin kita memahami “resep” di balik persamaan ini. Inilah seni dari persamaan diferensial — belajar dengan cara yang menyerupai seni menciptakan sesuatu yang artistik. Dengan pemahaman ini, kita tidak hanya menjadi pengamat pasif, tetapi juga pencipta aktif yang ikut menentukan bagaimana dunia terlihat dan berfungsi.

Jangan sampai ketinggalan, mari tingkatkan wawasan Anda dan terlibat langsung dalam komunitas yang memanfaatkan persamaan diferensial. Tantangan dan petualangan baru menanti Anda, membuka jalan menuju kemungkinan tanpa batas. Seolah-olah kita telah menemukan mesin waktu yang memungkinkan kita menjelajahi misteri masa lalu dan memprediksi masa depan. Dengan begitu banyak alat dan sumber daya yang tersedia, persamaan diferensial siap untuk mengguncang dunia Anda — dan Anda siap untuk itu!

Pembahasan Medan: Persamaan Diferensial dan Perannya

Paragraf kedua akan menyelidiki bagaimana persamaan diferensial mendukung inovasi teknologi. Mulai dari analisis data besar hingga kecerdasan buatan, perkembangan modern ini dipengaruhi oleh kemampuan kita untuk memecahkan persamaan diferensial yang kompleks. Berpikir tentang robotika atau kendaraan otonom? Ya, di balik layar banyak matematikawan yang bekerja tanpa henti menggunakan pendalaman persamaan diferensial untuk mengasah kemampuan mesin tersebut. Bersiaplah untuk taraf kehidupan yang lebih efisien dan cerdas dengan adanya inovasi ini.

Di urutan ketiga, mari kita analisis dari sudut pandang pendidikan dan pelatihan. Pendidikan formal sering kali menjadikan persamaan diferensial sebagai salah satu materi pokok. Ini karena pemahaman yang baik mengenai persamaan ini memberikan kemampuan kritis dalam menyelesaikan masalah nyata. Sebagai murid, mendapatkan keahlian ini memungkinkan Anda untuk siap menghadapi berbagai tantangan akademik dan profesional yang ada di depan. Dukungan dari pendidik yang terampil juga memegang peran vital dalam keberhasilan pembelajaran mengenai topik ini.

Di seluruh perjalanan ini, mari kita berikan spotlight pada bagaimana persamaan diferensial tak hanya berbicara soal angka dan rumus, namun juga mendorong kita untuk berpikir lebih mendalam dan analitik. Dalam mengolah data hingga menyusun strategi, persamaan diferensial menjadikan banyak metodenya dasar yang kokoh bagi kita. Jika Anda penasaran dan ingin menggali lebih dalam, tak ada salahnya untuk mulai mengeksplorasi dunia yang penuh kejutan ini. Bersama dengan persamaan diferensial, mari kita sambut masa depan yang penuh dengan kemungkinan dan keajaiban yang sebelumnya tak pernah kita bayangkan.

Dengan kreatifitas dan usaha, Anda juga bisa menjadi bagian dari cerita besar ini. Persamaan diferensial menantang kita untuk terlibat aktif dan berpikir di luar batas. Kemajuan dalam bidang ini sering kali datang dari mereka yang memiliki motivasi untuk belajar dan berbagi. Jadi, apa lagi yang Anda tunggu? Bergabunglah dengan revolusi matematika dan jadilah inspirasi bagi generasi berikutnya. Nikmati setiap langkah dalam perjalanan ini, dan bersiaplah melihat dunia dengan cara yang lebih menakjubkan dan inovatif!