ABSTRAK
Fungsi Green telah menjadi alat untuk menganalisis efek geomekanik reservoir yang penting seperti penurunan, pemadatan, penutupan sumur, dan variasi permeabilitas. Namun, fungsi Green klasik terkait dengan media elastis linier, homogen, dan disederhanakan secara geometris. Penggunaan fungsi tambahan yang mempertimbangkan media heterogen berpotensi menyederhanakan analisis numerik dari beberapa masalah yang kompleks. Karya penelitian ini mengusulkan pendekatan baru terhadap metode fungsi Green berdasarkan jaringan saraf tiruan (ANN) untuk mempertimbangkan media berlapis dengan aplikasi langsung dalam geomekanik reservoir. Solusi yang diperoleh melalui ANN ini memiliki keluaran berupa perpindahan yang dinormalkan pada setiap titik massif berlapis karena penerapan beban titik di dalam massif. Data masukan dari ANN yang diusulkan adalah sifat material media, beban titik, dan titik yang diminati. Dengan menggunakan fungsi Green berbasis ANN yang dikembangkan bersama dengan pendekatan fungsi Green klasik, dimungkinkan untuk memperoleh perpindahan secara individual pada setiap titik massif karena variasi tekanan pori dalam reservoir, hanya mendiskritisasi batas reservoir. Hal ini menghasilkan metode yang lebih efisien jika dibandingkan dengan metode tradisional, seperti metode elemen hingga. Untuk titik-titik yang menarik, dasar laut, serta bagian atas dan bawah reservoir, contoh numerik yang disajikan 25 kali lebih cepat daripada pendekatan fungsi Green klasik pada komputer dengan 12 thread 2,6 GHz dan RAM 32 GB. Pengurangan waktu pemrosesan ini sangat penting bagi para pengambil keputusan untuk bertindak dalam aplikasi lapangan.
1 Pendahuluan
Fungsi Green secara tradisional dikenal sebagai solusi persamaan diferensial akibat gangguan titik dalam suatu medium dalam beberapa aplikasi dan untuk persamaan diferensial kesetimbangan statis, yang menarik dalam karya ini. Fungsi-fungsi ini juga merupakan dasar untuk metode numerik klasik seperti metode elemen batas dan metode tanpa jaring.
Fungsi Green yang biasa diformulasikan untuk media homogen karena kompleksitas dalam memperoleh ekspresi analitis untuk media yang lebih generik. Salah satu cara untuk mengatasi hambatan ini adalah dengan menghitung fungsi Green secara numerik. Namun, untuk beberapa aplikasi, seperti dinamika fluida [ 1 ], geofisika [ 2 ], dan mekanika rekahan [ 3 ], kebutuhan untuk memecahkan fungsi Green secara numerik dan kemudian menerapkannya pada masalah yang dimaksud menjadi mahal secara komputasi. Solusi untuk situasi ini adalah penggunaan Kecerdasan Buatan (AI) sebagai proksi fungsi Green untuk distribusi material yang lebih generik melalui media. Satu kelas algoritma AI yang dapat digunakan untuk tujuan ini terdiri dari jaringan saraf tiruan (ANN). Karena ini adalah algoritma yang dipilih untuk pekerjaan ini, metode yang dikembangkan disebut sebagai fungsi Green berbasis ANN.
Meskipun fungsi Green dan AI merupakan dua topik penelitian klasik, baru-baru ini keduanya dibahas secara berpasangan. Penggabungan ini telah memberikan kontribusi pada studi persamaan diferensial secara umum [ 4 – 6 ] dan juga pada masalah-masalah spesifik seperti misalnya pada penyelesaian persamaan gelombang [ 7 ], simulasi fusi [ 8 ], estimasi dosis radiasi [ 9 ] dan transformasi koordinat untuk linearisasi masalah nilai batas nonlinier [ 10 ].
Meskipun demikian, tidak ditemukan karya penelitian yang secara khusus menggabungkan AI dan fungsi Green yang diterapkan pada geomekanik. Faktanya, AI telah diterapkan secara luas pada masalah mekanik dan geomekanik, melalui pendekatan lain. Aplikasi umum AI di area ini adalah penggantian perhitungan klasik yang memakan waktu dengan model AI [ 11 ]. Pendekatan ini dapat diamati dalam masalah geomekanik dengan tujuan yang berbeda seperti optimasi proses produksi minyak dan gas [ 12 , 13 ], desain sumur [ 14 ], pengeboran sumur [ 15 ], dan injeksi karbon dioksida [ 16 – 18 ]. Model pengganti AI juga digunakan dalam simulasi material multiskala [ 19 – 22 ], simulasi aliran-geomekanik yang digabungkan [ 23 , 24 ], analisis risiko dan keandalan geomekanik [ 25 – 28 ], dan analisis invers geomekanik [ 29 – 34 ]. Kopling antara AI dan fungsi Green memiliki karakteristik utamanya, dibandingkan dengan strategi model pengganti, kemampuan untuk menerapkannya pada masalah dengan geometri dan distribusi material yang berbeda tanpa perlu pelatihan baru. Untuk alasan ini, penelitian ini mengusulkan penggunaan ANN sebagai proksi fungsi Green generik untuk menghitung medan perpindahan dalam massa batuan karena variasi tekanan pori dalam reservoir geomekanik. Penggunaan fungsi Green sederhana untuk setengah ruang homogen elastis linier adalah pendekatan numerik untuk memprediksi medan perpindahan yang dihasilkan dari variasi tekanan pori reservoir [ 35 ]. Namun , ada metode klasik numerik dan analitis lainnya, dengan kekhususannya, untuk tujuan ini. Model analitis klasik untuk prediksi penurunan tanah dikembangkan oleh Geertsma [ 36-39 ], berdasarkan prinsip inti regangan yang diperkenalkan oleh Mindlin dan Cheng [ 40 , 41 ] . Model Geertsma memprediksi penurunan tanah karena penipisan reservoir silinder dalam massa semi-tak terbatas elastis linier. Van Opstal [ 42 ] memperluas model ini untuk memperhitungkan basis kaku, mewakili batuan kristal atau karbonat kaku, sementara Tempone [ 43 ] lebih menyempurnakannya untuk menghitung medan perpindahan dan regangan di seluruh massa.
Berdasarkan karya Geertsma, Segall [ 44 ] mengembangkan model analitis untuk mengevaluasi regangan dan tegangan di sekitar reservoir axisymmetric yang mengalami variasi tekanan pori. Soltanzadeh dan Hawkes [ 45 ], berdasarkan teori inklusi Eshelby [ 46 – 48 ], membahas reservoir elips dan persegi panjang 2D. Untuk generalisasi geometri lebih lanjut, Muñoz dan Roehl [ 49 ] mengusulkan model untuk reservoir 3D dengan geometri sembarang, menghilangkan kebutuhan untuk integrasi fungsi singular. Model-model ini mengasumsikan reservoir yang tertanam dalam media homogen, elastis linier, dan semi-tak terbatas.
Skenario stratigrafi yang lebih kompleks dibahas oleh Du dan Olson [ 50 ], Mehrabian dan Abousleiman [ 51 ], dan Wangen dan Halvorsen [ 52 ], yang menganalisis medan perpindahan dan regangan dalam media tiga lapis yang dipengaruhi oleh reservoir silinder. Mehrabian dan Abousleiman [ 51 ] juga menunjukkan skalabilitas model mereka terhadap stratigrafi berlapis-lapis. Fokker dan Orlic [ 53 ] memajukan pendekatan ini dengan model semi-analitis yang menggabungkan beberapa lapisan viskoelastis.
Bahasa Indonesia: Dibandingkan dengan pendekatan analitis atau semi-analitis, metode numerik menyediakan fleksibilitas yang lebih besar, memungkinkan simulasi geometri kompleks, perilaku material, dan masalah geomekanika aliran yang terkopel. Metode elemen hingga (FEM) [ 54 – 57 ] digunakan secara luas karena kemampuannya menangani nonlinier seperti plastisitas [ 58 , 59 ], viskositas [ 60 , 61 ], rekahan [ 62 ], dan reaktivasi patahan [ 63 ] dalam simulasi geomekanika reservoir. Namun, solusi numerik dari jenis masalah ini memerlukan diskritisasi geometri pada wilayah besar di luar sekitar reservoir, yang secara signifikan meningkatkan biaya komputasi. Dengan demikian, memilih metode yang tepat untuk analisis geomekanik tersebut melibatkan pertimbangan pilihan: metode yang lebih baik mewakili geometri, distribusi material, dan propertinya tetapi menuntut sumber daya komputasi yang lebih tinggi, versus metode yang memberikan hasil yang disederhanakan tetapi lebih cepat. Dalam konteks ini, penggunaan fungsi Green berbasis ANN untuk media heterogen muncul sebagai pendekatan yang mempertahankan kemampuan generalisasi solusi numerik klasik sambil mengurangi biaya komputasi.
Dibandingkan dengan pendekatan fungsi Green yang homogen, penggunaan fungsi Green untuk media heterogen dapat mengurangi biaya komputasi untuk masalah geomekanik reservoir dengan menghindari kebutuhan untuk memecahkan sistem persamaan nonlinier. Lebih jauh, pendekatan fungsi Green berbasis ANN yang diusulkan juga mengurangi upaya komputasi karena hanya menuntut diskritisasi reservoir, sedangkan pendekatan fungsi Green elastis linier tradisional menuntut diskritisasi reservoir dan daerah di sekitarnya. Dengan demikian, karya penelitian ini meningkatkan pendekatan fungsi Green menggunakan ANN untuk mencapai fungsi Green untuk media terstratifikasi. ANN yang digunakan adalah jenis Perceptron multilayer (jaringan saraf umpan maju), dan pelatihannya didasarkan pada basis data yang terdiri dari solusi numerik dari beberapa masalah yang menggunakan fungsi Green yang diterapkan pada media terstratifikasi heterogen.
2 Pendekatan Fungsi Green untuk Geomekanika Reservoir
Pendekatan fungsi Green untuk geomekanika reservoir didasarkan pada teorema resiprositas, yang menghubungkan penyelesaian dua sistem, satu sistem bantu dan satu sistem yang diminati. Sistem bantu memiliki penyelesaian fungsi Green, dan sistem yang diminati adalah masalah geomekanika reservoir yang harus dipecahkan. Demi ilustrasi, tanpa kehilangan keumuman, perhatikan fungsi Green untuk gaya yang diterapkan dalam media semi-tak terbatas elastis linier (Solusi Fundamental Melan), yang ditunjukkan dalam Lampiran A , dan masalah yang diminati adalah reservoir geomekanik dengan variasi tekanan pori yang terletak di zona berlapis yang tertanam dalam media semi-tak terbatas (Gambar 1 ).
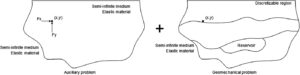
Meskipun solusi fundamental Melan mempertimbangkan medium elastis linier homogen semi-tak terbatas, solusi tersebut dapat digunakan oleh metode fungsi Green untuk memecahkan masalah heterogen yang terdiri dari material elastis, linear dan non-linear, dan material visko-plastik. Untuk melakukan ini, perlu dipahami konsep tegangan komplementer untuk situasi heterogenitas dan visko-plastisitas, yang diperoleh dari hubungan konstitutif.
2.1 Poroelastisitas Linier yang Diterapkan pada Masalah Heterogen
Medan tegangan dihitung berdasarkan prinsip tegangan ekivalen, yang mana persamaan ( 1 ) berlaku untuknya.

2.2 Poro-visko-plastisitas
Variasi tekanan pori reservoir dapat menyebabkan deformasi permanen, sehingga hubungan elastisitas linier pada Persamaan ( 1 ) harus dimodifikasi untuk memperhitungkan karakteristik ini, yang mengarah ke Persamaan ( 5 ).





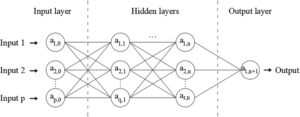

3.1 Data Input dan Output
Jaringan saraf yang digunakan sebagai proksi fungsi Green untuk media berstrata memiliki parameter masukan sebagai berikut:
- lima rasio Poisson, satu untuk setiap lapisan;
- lima modulus elastisitas dinormalisasi oleh modulus elastisitas lapisan terakhir;
- ketebalan empat lapisan, karena lapisan terakhir selalu memiliki ketebalan tak terhingga;
- kedalaman di mana beban titik diterapkan; dan
- posisi relatif antara titik evaluasi dan titik beban.
Empat ANN dilatih, satu untuk masing-masing dari empat perpindahan yang dipertimbangkan (perpindahan vertikal atau horizontal karena gaya satuan vertikal atau horizontal). Selain itu, data keluaran dinormalisasi, mengikuti Persamaan ( 19 ), untuk menjaga besarnya mendekati satuan, sehingga meningkatkan efisiensi proses pelatihan.

3.2 Pembuatan Set Data
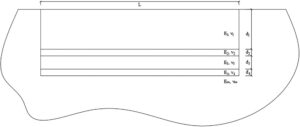
Untuk melatih jaringan saraf, diperlukan seperangkat data masukan yang kuat dan data keluarannya masing-masing, yang secara tepat mengkarakterisasi fenomena yang akan digunakan jaringan tersebut. Untuk melatih jaringan yang digunakan dalam penelitian ini, perlu dibangun basis data yang berisi perpindahan vertikal dan horizontal yang disebabkan oleh gaya unit vertikal dan horizontal, yang diterapkan pada lingkungan yang terstratifikasi seperti yang ditunjukkan pada Gambar 3. Perpindahan tersebut dihitung secara numerik untuk 45 media terstratifikasi yang berbeda, agar ANN mampu digeneralisasi ke stratigrafi yang berbeda.
Perpindahan yang digunakan untuk melatih ANN diperoleh secara numerik dari Persamaan ( 20 ), yang dapat diperoleh berdasarkan teorema resiprositas yang analog dengan Persamaan ( 14 ), tetapi untuk kasus ini, sistem yang dimaksud adalah model stratifikasi yang dikenai beban titik. Untuk setiap media yang dipertimbangkan, beban titik diposisikan pada 33 kedalaman yang berbeda dan, untuk setiap posisi, perpindahan pada 500 titik dalam domain dievaluasi, dengan total 16.500 set data untuk setiap 45 stratigrafi.
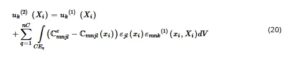
3.3 Pelatihan Jaringan Syaraf
Untuk pelatihan jaringan saraf, data dihasilkan oleh 45 model berbeda, yang dibagi lagi menjadi 3 kelompok, yaitu kelompok pelatihan, kelompok validasi, dan kelompok uji, yang masing-masing sesuai dengan 70%, 15%, dan 15% dari total jumlah data. Sifat elastis yang dipertimbangkan bervariasi dari 0,1 hingga 0,4 untuk rasio Poisson, dan dari 5 hingga 60 GPa untuk modulus elastis. Rentang ini dipilih karena mencakup sifat-sifat material elastis bawah permukaan yang khas.
Proses pelatihan secara tradisional terdiri dari mendefinisikan bobot dan bias yang menghasilkan hasil yang sesuai dengan data pelatihan. Dengan demikian, proses ini dapat dipahami sebagai optimasi di mana fungsi tujuan adalah ukuran kesalahan antara keluaran yang diperoleh oleh kelompok pelatihan dan keluaran yang diprediksi oleh ANN. Namun, untuk menjamin kapasitas ekstrapolasi untuk data lain selain yang berasal dari kelompok pelatihan, metode penghentian awal [ 65 ] sebagai teknik regularisasi digunakan. Metode ini menggunakan kelompok validasi di setiap iterasi pelatihan untuk memverifikasi apakah overfitting terjadi, yaitu, mencegah model ANN beradaptasi dengan data pelatihan tanpa beradaptasi dengan data kelompok validasi. Dalam artikel ini, pengukuran kesalahan yang dipertimbangkan adalah kesalahan kuadrat rata-rata. Dengan demikian, fungsi kerugian ditunjukkan pada Persamaan ( 21 ).

Selain proses pelatihan yang melibatkan kalibrasi bobot dan bias, juga perlu untuk mendefinisikan jumlah lapisan tersembunyi, jumlah neuron per lapisan tersembunyi, dan fungsi aktivasi yang akan digunakan dalam masalah tersebut. Ini dicapai dengan menggunakan proses pelatihan iteratif berdasarkan pencarian Bayesian [ 68 ]. Prosedur yang diadopsi ini pada dasarnya adalah Optimasi Bayesian di mana fungsi objektif adalah metrik kesalahan yang dihitung untuk set data validasi, dan variabelnya adalah fungsi aktivasi, jumlah lapisan tersembunyi, dan jumlah neuron per lapisan tersembunyi. Metodologi tersebut terdiri dari pelatihan jaringan yang berbeda, di mana, untuk setiap jaringan yang dilatih, topologi jaringan berikutnya didefinisikan sedemikian rupa sehingga kesalahan absolut rata-rata yang dihitung berdasarkan basis data validasi memiliki probabilitas lebih besar untuk menjadi lebih kecil daripada jaringan yang dilatih hingga saat itu. Selama proses ini, dianggap bahwa jaringan saraf akan memiliki antara tiga dan delapan lapisan tersembunyi dan antara 1 dan 300 neuron per lapisan tersembunyi. Pertimbangan ini terkait erat dengan jumlah data untuk pelatihan, dan akibatnya, terkait dengan jumlah stratigrafi yang dihasilkan untuk pelatihan. Dengan mempertimbangkan 45 stratigrafi yang berbeda dan mengevaluasi perpindahan pada 500 titik karena beban yang diterapkan pada 33 kedalaman yang berbeda, set basis data memiliki 742.500 set data, yang 519.750 di antaranya digunakan untuk pelatihan. Jumlah data ini dipertimbangkan karena memiliki besaran yang sama dengan jumlah parameter (bobot dan bias) yang diperlukan untuk mengkalibrasi jaringan saraf yang memiliki tiga lapisan tersembunyi yang terdiri dari 200 neuron (567.200).
Akhirnya, jaringan yang menunjukkan kinerja terbaik dipilih. Jaringan saraf ini menggunakan fungsi Relu sebagai fungsi aktivasi untuk input dan untuk lapisan tersembunyi, dan fungsi linier sebagai fungsi aktivasi untuk lapisan output. Jumlah neuron di setiap lapisan dan jumlah total bobot dan bias disajikan dalam Tabel 1. Jaringan saraf dilatih untuk menjadi proksi
menyajikan jumlah bobot dan bias terbesar (118.328), yang kira-kira lima kali lebih kecil dari jumlah data dalam set data yang digunakan untuk pelatihan (519.750). Kapasitas generalisasi jaringan saraf diverifikasi melalui contoh numerik yang parameternya berbeda dari yang digunakan untuk pelatihan. Proses pelatihan untuk setiap jaringan saraf memakan waktu sekitar 24 jam pada komputer dengan 12 utas 2,6 GHz dan RAM 32 GB.
| Keluaran | Neuron per lapisan | Jumlah total bobot dan bias |
|---|---|---|
| u11¯ | 17–242–104–116–92–1 | 52.110 orang |
| u21¯ | 17–221–94–262–263–1 | 118.328 orang |
| u12¯ | 17–217–198–68–83–72–5–264–1 | 73.683 orang |
| u22¯ | 17–97–244–76–179–1 | 57.644 orang |
4 Contoh Numerik
Bahasa Indonesia: Di bagian ini, aplikasi fungsi Green dari jaringan saraf disajikan. Contoh ini terdiri dari reservoir berbentuk persegi panjang yang menipis menjadi stratigrafi empat lapis. Lapisan atas disebut lapisan penutup, lapisan kedua adalah batuan penutup, lapisan ketiga adalah tempat reservoir tertanam, dan lapisan keempat adalah substratum, seperti yang ditunjukkan pada Gambar 4. Garis putus-putus pada Gambar 4 mewakili batas reservoir sementara huruf “L”, “R”, “T”, dan “B” mewakili sisi kiri, sisi kanan, bagian atas, dan bagian bawah reservoir. Seluruh model tertanam dalam media semi-tak terbatas yang lebih kaku daripada lapisan lainnya, dan semua material bersifat elastis linier dengan sifat-sifat yang ditunjukkan pada Tabel 2. Tekanan awal meluruh di dalam reservoir, tetapi tetap konstan di luar, yang merupakan perilaku umum reservoir selama ekstraksi minyak dan gas.
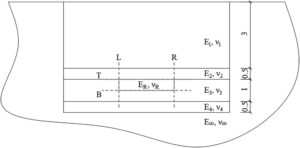
| Notasi | Definisi | Nilai | Satuan |
|---|---|---|---|
| Lapisan 1 | |||
| E1 | Modulus elastisitas | 34 | IPK |
| ν1 | Rasio Poisson | 0,25 | — |
| Lapisan 2 | |||
| E2 | Modulus elastisitas | 46 | IPK |
| ν2 | Rasio Poisson | 0.23 | — |
| Lapisan 3 | |||
| E3 | Modulus elastisitas | 7 | IPK |
| ν3 | Rasio Poisson | 0.33 | — |
| Waduk | |||
| ER | Modulus elastisitas | 7 | IPK |
| νR | Rasio Poisson | 0.33 | — |
| α | Koefisien Biot | 0.8 | — |
| ΔPp | Perubahan tekanan pori | -10 | MPa |
| Lapisan 4 | |||
| E4 | Modulus elastisitas | 38 | IPK |
| ν4 | Rasio Poisson | 0.34 | — |
| Media semi tak terbatas | |||
| E∞ | Modulus elastisitas | 46 | IPK |
| ν∞ | Rasio Poisson | 0.20 | — |
Contoh ini diselesaikan dengan pendekatan fungsi Green klasik untuk media heterogen [ 35 ], yang menerapkan fungsi Green homogen, dan dengan pendekatan fungsi Green berbasis ANN, yang menerapkan ANN sebagai proksi fungsi Green heterogen. Kedua hasil didiskusikan dan dibandingkan dalam hubungan akurasi dan waktu pemrosesan. Diskritisasi yang dipertimbangkan untuk pendekatan klasik memiliki 2880 elemen dan 3066 derajat kebebasan, dan integrasi numerik yang diadopsi adalah kuadratur Bartholomew level 3 [ 69 ]. Untuk pendekatan berbasis ANN, model didiskritisasi dalam 44 elemen linier di sekitar reservoir, dengan aturan kuadratur Gauss tiga titik untuk integrasi numerik.
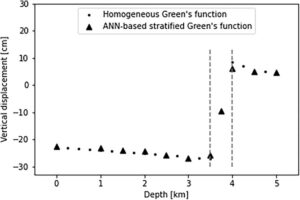
Gambar 5 menunjukkan perpindahan vertikal di bagian tengah model sepanjang kedalaman model, dengan titik awal berada di permukaan dan titik akhir pada kedalaman −5000 m, yang mewakili kontak antara lapisan terakhir dan media semi-tak terbatas. Pendekatan fungsi Green berbasis ANN yang diusulkan menyajikan hasil yang serupa dengan yang diperoleh menggunakan pendekatan klasik. Diamati dua titik di mana fungsi Green jaringan saraf memiliki presisi yang berkurang, di bagian atas ( y = −3500 m) dan di bagian bawah reservoir ( y = −4000 m).
Gambar 6 menunjukkan perpindahan vertikal sepanjang lebar model di permukaan (a), di reservoir atas (b) ( y = −3500 m), dan di reservoir bawah (c) ( y = −4000 m). Hasil penurunan menunjukkan kesesuaian yang baik antara pendekatan klasik dan jaringan saraf. Untuk reservoir atas dan bawah, bentuk fungsi dapat ditiru, tetapi terlihat adanya celah antara kurva klasik dan jaringan saraf di dalam lebar reservoir.

Gambar 7 menunjukkan perpindahan horizontal sepanjang lebar model di permukaan (a), di reservoir atas (b) ( y = −3500 m), dan di reservoir bawah (c) ( y = −4000 m). Dapat diamati bahwa ada kesesuaian yang baik antara kedua pendekatan di permukaan. Di reservoir atas, kedua kurva sedikit berbeda, tetapi mereka menunjukkan kesamaan seperti puncak di sudut atas (dengan besaran yang berbeda) dan perpindahan horizontal nol di tengah. Mengamati perpindahan horizontal di dasar reservoir, perpindahan maksimum untuk kedalaman ini sesuai dalam dua pendekatan, dan bentuk kurva serupa dalam kedua kasus.

Singkatnya, pendekatan fungsi Green berbasis ANN dapat memberikan perpindahan yang konsisten dengan perpindahan yang diperoleh menggunakan pendekatan klasik. Perbedaan utama antara kedua pendekatan tersebut adalah waktu CPU yang dibutuhkan, yang berkurang hingga 25% dalam 12 utas perangkat keras 2,6 GHz untuk pendekatan jaringan saraf jika dibandingkan dengan pendekatan klasik. Penting untuk menyoroti bahwa untuk mendapatkan solusi menggunakan fungsi Green berbasis ANN, ada juga upaya komputasi untuk membangun basis data dan melatih masing-masing dari empat jaringan saraf. Oleh karena itu, jika perlu untuk setiap masalah baru untuk menghasilkan set data baru dan melakukan pelatihan baru, metode yang diusulkan akan jauh lebih mahal. Namun, jaringan saraf yang dilatih dapat digunakan untuk masalah lain yang memiliki karakteristik yang sama dengan set data yang dilatihnya. Dengan cara ini, penghematan waktu yang efektif akan terjadi untuk masalah stratigrafi yang memiliki lapisan horizontal dan hingga lima material yang berbeda, terlepas dari posisi dan bentuk reservoir.
5 Kesimpulan
Penggunaan jaringan saraf sebagai proksi untuk fungsi Green memungkinkan untuk memperoleh solusi fundamental umum secara lebih efisien jika dibandingkan dengan metode klasik. Dengan menggunakan fungsi saraf Green ini, dimungkinkan untuk menghitung medan perpindahan karena variasi tekanan pori reservoir, dengan hanya mendiskritisasi reservoir batas, sedangkan pendekatan klasik menuntut diskritisasi seluruh massa di dekat reservoir. Karena itu, dimungkinkan untuk menghitung perpindahan di setiap titik massa tanpa perlu menghitung perpindahan di titik lain dari model. Selain itu, dalam pendekatan yang diusulkan, proses iteratif yang digunakan dalam pendekatan klasik tidak diperlukan.
Aplikasi numerik terdiri dari reservoir penipisan seragam yang tertanam dalam masif empat lapis, yang merupakan konfigurasi stratigrafi pra-ladang garam yang khas (dasar laut, albian, garam, dan lapisan bawah tanah). Pendekatan fungsi Green menuntut diskritisasi batas reservoir dalam 44 elemen linier unidimensional, sedangkan pendekatan tradisional menuntut jaring dengan 2880 elemen dan 3066 derajat kebebasan. Perpindahan yang diperoleh oleh kedua metode tersebut serupa. Ini memvalidasi keandalan fungsi Green jaringan saraf yang diusulkan, karena data yang digunakan dalam aplikasi berbeda dari data yang digunakan untuk pelatihan jaringan saraf. Jadi, diharapkan bahwa untuk contoh geomekanika reservoir lainnya, pendekatan ini juga akan menghasilkan hasil yang andal.
Pendekatan fungsi Green neural yang diusulkan dapat diperluas ke masalah tiga dimensi non-elastis, dan ke lapisan non-horizontal. Namun, untuk membuatnya layak, perlu untuk meningkatkan kompleksitas pelatihan ANN dan mengembangkan strategi parameterisasi lainnya. Misalnya, penerapan pendekatan fungsi Green berbasis ANN untuk masalah tiga dimensi dengan distribusi material generik memerlukan penggunaan jaringan saraf konvolusi, yang memungkinkan penerapan parameterisasi generik dari distribusi properti spasial. Untuk masalah yang melibatkan material non-elastis, set data pelatihan harus terdiri dari solusi numerik media nonlinier, yang dapat memakan waktu dan menuntut penggunaan jaringan saraf berulang untuk menangkap ketergantungan lintasan material ini. Namun, setelah jaringan dilatih, penggunaan fungsi Green berbasis ANN akan identik dengan apa yang disajikan dalam contoh yang diberikan, selama penerapannya memiliki karakteristik yang mengikuti kriteria yang sama dengan set data pelatihan.
Akhirnya, diamati bahwa metode yang diusulkan menawarkan perolehan kinerja komputasi yang signifikan, yang sangat berharga untuk memperoleh hasil yang mendukung pengambilan keputusan yang peka terhadap waktu selama pengembangan reservoir. Selain itu, efisiensi komputasi ini menjadi keuntungan utama saat melakukan analisis stokastik atau optimasi, karena analisis tersebut biasanya memerlukan ribuan simulasi numerik. Sementara percepatan merupakan manfaat yang jelas dari pendekatan fungsi Green berbasis ANN, aspek yang paling penting adalah memahami sumber keuntungan ini. Peningkatan kinerja dicapai karena metode ini memungkinkan penghitungan komponen vektor perpindahan apa pun di titik mana pun dalam model tanpa perlu menghitung seluruh medan perpindahan, seperti yang diperlukan dalam metode elemen hingga. Oleh karena itu, tergantung pada jumlah titik minat yang akan dievaluasi, perolehan komputasi dapat jauh lebih besar daripada perolehan yang diamati dalam contoh numerik. Karakteristik ini dimungkinkan oleh kemampuan untuk memperoleh solusi fundamental generik menggunakan ANN, yang memungkinkan persamaan perpindahan diformulasikan hanya dalam hal parameter input seperti koefisien Biot, variasi tekanan pori, dan solusi fundamental yang direpresentasikan oleh jaringan saraf.