ABSTRAK
Pemanfaatan data kontrol non-konkuren (NCC) dalam analisis lengan yang masuk terlambat dalam uji coba platform baru-baru ini telah mendapat perhatian yang cukup besar. Meskipun menggabungkan NCC dapat menghasilkan peningkatan daya dan ukuran sampel yang lebih rendah, NCC dapat menimbulkan bias pada penaksir efek jika terdapat pergeseran temporal. Bertujuan untuk mengurangi potensi bias ini, kami mengusulkan berbagai pendekatan berbasis model frekuentis yang memanfaatkan NCC, sambil menyesuaikan waktu. Salah satu model yang tersedia saat ini menggabungkan waktu sebagai efek tetap kategoris, yang memisahkan durasi uji coba menjadi beberapa periode, yang didefinisikan sebagai interval waktu yang dibatasi oleh lengan mana pun yang memasuki atau meninggalkan platform. Dalam karya ini, kami mengusulkan dua perluasan model ini. Pertama, kami mempertimbangkan definisi waktu alternatif dengan membagi uji coba menjadi interval waktu kalender dengan panjang tetap. Kedua, kami mengusulkan penyesuaian waktu berbasis model alternatif. Secara khusus, kami menyelidiki penyesuaian efek acak dan menggunakan spline untuk memodelkan waktu dengan fungsi polinomial. Kami mengevaluasi kinerja pendekatan yang diusulkan dalam studi simulasi dan mengilustrasikan penggunaannya melalui studi kasus. Kami menunjukkan bahwa penyesuaian waktu melalui fungsi spline mengendalikan kesalahan tipe I dalam uji coba dengan pola tren waktu yang cukup mulus dan dapat menghasilkan peningkatan daya dibandingkan dengan model efek tetap standar. Namun, model efek tetap dengan penyesuaian periode adalah model yang paling tangguh untuk tren waktu arbitrer, asalkan trennya sama di semua cabang. Khususnya, dalam uji coba dengan perubahan mendadak dalam tren waktu, model penyesuaian periode lebih disukai jika NCC disertakan.
1 Pendahuluan
Uji coba platform mempercepat pengembangan obat dengan menawarkan peningkatan fleksibilitas dan efisiensi (Koenig et al. 2024 ). Mereka mengevaluasi kemanjuran beberapa lengan pengobatan di bawah protokol utama tunggal, dengan manfaat tambahan yang memungkinkan lengan pengobatan untuk memasuki uji coba dari waktu ke waktu dan untuk berhenti lebih awal berdasarkan data sementara (Woodcock dan LaVange 2017 ). Desain ini memungkinkan evaluasi yang lebih cepat dari obat-obatan yang sedang dikembangkan, karena mereka dapat langsung dimasukkan ke platform bersama (Redman dan Allegra 2015 ). Selain itu, keuntungan efisiensi dapat dicapai dengan berbagi kelompok kontrol di seluruh platform. Pembagian sumber daya menurunkan jumlah pasien yang diperlukan dalam lengan kontrol serta jumlah keseluruhan pasien yang diperlukan untuk uji coba dibandingkan dengan uji coba yang berdiri sendiri. Ini memberikan keuntungan juga dari perspektif etika dan pasien (Saville dan Berry 2016 ). Mengingat kompleksitasnya, perancangan uji coba platform memerlukan simulasi komputer yang ekstensif dan penggunaan perangkat lunak untuk menilai karakteristik pengoperasiannya menjadi krusial untuk mengevaluasi ketahanan rancangan yang diusulkan di berbagai skenario (Meyer et al. 2020 ). Selain itu, inferensi statistik yang valid dalam uji coba platform tetap menjadi perhatian utama otoritas regulasi, karena beberapa tantangan muncul karena berbagai fitur adaptif, seperti penambahan lengan eksperimen yang terlambat (Lee et al. 2021 ).
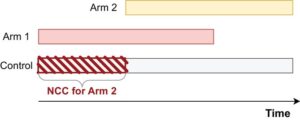
Khususnya, penggunaan kelompok kontrol umum dalam analisis statistik lengan tambahan telah menjadi subjek diskusi yang hidup (Bofill Roig et al. 2022 ; Dodd et al. 2021 ; Lee dan Wason 2020 ; Saville et al. 2022 ). Dalam uji coba platform, untuk lengan pengobatan yang masuk saat uji coba sedang berlangsung, kelompok kontrol dibagi menjadi dua kelompok terpisah: kontrol bersamaan (CC), yang mencakup pasien yang diacak ke lengan kontrol pada saat yang sama ketika lengan pengobatan yang diberikan menjadi bagian dari uji coba platform dan dengan demikian memiliki probabilitas alokasi positif untuk diacak ke lengan pengobatan yang diselidiki; dan kontrol tidak bersamaan (NCC), yang menunjukkan pasien yang diacak ke kelompok kontrol sebelum lengan pengobatan yang dievaluasi memasuki platform. Gambar 1 memberikan contoh uji coba platform dengan dua lengan eksperimen, di mana lengan kedua bergabung dengan uji coba di titik waktu berikutnya. Data NCC untuk lengan kedua ditandai dengan pola bergaris diagonal. Menyertakan data NCC dalam perbandingan perawatan–kontrol dapat memberikan beberapa manfaat, seperti ukuran sampel yang dibutuhkan lebih rendah atau peningkatan kekuatan statistik dibandingkan dengan analisis yang hanya berdasarkan CC. Akan tetapi, karena kelompok perawatan ditambahkan secara berurutan, pengacakan terjadi pada waktu yang berbeda. Kurangnya pengacakan yang sebenarnya dari waktu ke waktu dapat menyebabkan inflasi tingkat kesalahan tipe I dan dapat menimbulkan bias dalam penaksir efek perawatan karena tren waktu. Tren waktu dapat disebabkan, misalnya, oleh perubahan standar perawatan, populasi pasien, atau efek musiman (US Food and Drug Administration 2023 ).
Baru-baru ini, beberapa pendekatan pemodelan diusulkan untuk mengatasi tantangan dalam memanfaatkan data NCC, sambil tetap mengendalikan tingkat kesalahan tipe I dan tanpa memperkenalkan bias pada penaksir efek. Berfokus pada uji coba platform dengan dua lengan eksperimen, Lee dan Wason ( 2020 ) dan Bofill Roig et al. ( 2022 ) mempertimbangkan pendekatan pemodelan frekuentis, di mana waktu disertakan ke dalam model baik sebagai fungsi linier atau kovariat kategoris. Untuk yang terakhir, uji coba dibagi menjadi dua periode, dipisahkan oleh titik waktu di mana lengan eksperimen kedua ditambahkan ke platform. Ditunjukkan bahwa kedua model meningkatkan daya statistik dibandingkan dengan analisis menggunakan data CC saja dan mengendalikan tingkat kesalahan tipe I, jika bentuk fungsional tren waktu ditentukan dengan benar, tren waktu sama di semua lengan dan aditif pada skala model (Bofill Roig et al. 2022 ). Selain itu, model dengan penyesuaian kategoris secara asimtotik mempertahankan tingkat kesalahan tipe I bahkan di bawah kesalahan spesifikasi bentuk fungsional tren waktu, asalkan pengacakan blok digunakan. Untuk menangani situasi di mana tren waktu dapat berbeda antara lengan, Bofill Roig et al. ( 2022 ) juga menyelidiki model yang mencakup interaksi antara perawatan dan waktu. Namun, sementara model ini mempertahankan tingkat kesalahan tipe I juga dalam kasus dengan tren waktu yang berbeda, perolehan daya dari penggunaan data NCC hilang. Alternatif Bayesian disarankan oleh Saville et al. ( 2022 ) dalam apa yang disebut pendekatan Time Machine, yang menggunakan model hierarki Bayesian dan menyesuaikan waktu dalam bentuk interval (“bucket”) dengan panjang yang sama. Model tersebut memperhalus respons kontrol di seluruh bucket waktu, sehingga bucket yang lebih dekat dimodelkan dengan respons yang lebih mirip. Mereka menunjukkan bahwa Time Machine secara kasar mengontrol tingkat kesalahan tipe I dan menghasilkan kinerja yang lebih unggul dalam hal daya statistik dibandingkan dengan model frekuentis dengan penyesuaian kategoris untuk waktu dalam skenario dengan pola tren waktu linier. Marschner dan Schou ( 2022 ) mengusulkan untuk menganalisis uji coba platform menggunakan teknik meta-analisis, yang memungkinkan untuk melakukan perbandingan pengobatan-kontrol dan pengobatan-pengobatan untuk kelompok yang tidak aktif secara bersamaan dalam uji coba. Dalam pendekatan meta-analisis jaringan ini, uji coba platform dipandang sebagai jaringan perbandingan langsung (bersamaan), yang dibuat dalam periode antara adaptasi uji coba; dan perbandingan tidak langsung (tidak bersamaan), yang dibuat di beberapa tahap dalam uji coba menggunakan kelompok referensi umum. Estimasi perbandingan pengobatan-kontrol yang tidak bersamaan kemudian diperoleh dengan menggabungkan estimasi kontras langsung secara linier.
Dalam karya ini, kami memperluas strategi pemodelan frekuentis dari Bofill Roig et al. ( 2022 ). Secara khusus, kami mengusulkan definisi alternatif dari variabel waktu dan mempertimbangkan penyesuaian untuk interval waktu kalender yang berjarak sama, mirip dengan Mesin Waktu Bayesian, juga dalam pengaturan frekuentis. Selain itu, kami menyelidiki pendekatan pemodelan yang lebih maju, seperti model campuran atau spline polinomial. Asumsi tren waktu yang sama, yang diperlukan untuk semua metode yang diusulkan sejauh ini, mungkin tidak selalu berlaku dalam praktik, karena perubahan temporal dapat memengaruhi lengan pengobatan secara berbeda, misalnya, dalam pengaturan dengan varian penyakit yang berbeda. Oleh karena itu, kami menyelidiki apakah asumsi ini dapat dilonggarkan dengan mempertimbangkan model campuran, yang mencakup interaksi antara pengobatan dan waktu sebagai efek acak. Kinerja metode yang diusulkan dievaluasi dalam studi simulasi, di mana kami juga menilai kondisi di mana pendekatan mengarah pada inferensi statistik yang valid. Penggunaan metode yang dipertimbangkan ditunjukkan pada kumpulan data dunia nyata dari uji klinis untuk penyakit langka (kelumpuhan supranuklear progresif [PSP]), dan dalam studi hipotetis berdasarkan uji coba platform nyata untuk leukemia limfositik kronis (disajikan dalam Informasi Pendukung, Bagian D ).
Sisa dari makalah ini disusun sebagai berikut: Bagian 2 memperkenalkan notasi dan desain uji coba yang dipertimbangkan dan menjelaskan metode yang diusulkan untuk uji coba platform dengan tren waktu yang sama di semua lengan. Di Bagian 3 , kami membahas kemungkinan perluasan ke uji coba di mana perubahan temporal memengaruhi lengan secara berbeda. Bagian 4 menyajikan studi simulasi yang ekstensif, mengevaluasi karakteristik pengoperasian metode yang dipertimbangkan dalam berbagai pengaturan. Penggunaan strategi pemodelan dicontohkan dalam dua studi kasus menggunakan data tentang penyakit neurodegeneratif langka dan jenis kanker darah, yang disajikan di Bagian 5. Kami menyimpulkan makalah ini dengan diskusi dan kesimpulan di Bagian 6 .
2 Metode






3 Ekstensi untuk Melonggarkan Asumsi Tren Waktu yang Sama
Pendekatan pemodelan yang diuraikan dalam bagian sebelumnya, serta semua pendekatan pemodelan lain yang tersedia hingga saat ini untuk memanfaatkan NCC, bergantung pada asumsi tren waktu yang sama di semua cabang dalam uji coba platform pada skala model (Bofill Roig et al. 2022 ). Pelanggaran asumsi ini dapat menyebabkan hilangnya kontrol tingkat kesalahan tipe I dan estimasi efek perlakuan yang bias. Di bagian ini, kami mengusulkan metode analisis yang dapat mengurangi potensi bias dalam uji coba di mana terdapat tren waktu yang berbeda di seluruh cabang.
Secara khusus, kami memperluas model campuran dari Bagian 2.3 dan mempertimbangkan model campuran dengan perlakuan dan waktu sebagai efek tetap kategoris (menggunakan definisi periode variabel waktu, serta interval waktu kalender) dan interaksi antara variabel-variabel ini sebagai efek acak. Model yang disesuaikan untuk periode didefinisikan sebagai berikut:

Model-model ini memperkirakan perbedaan dalam respons rata-rata di setiap kelompok perlakuan relatif terhadap kontrol dan setiap periode/unit waktu kalender relatif terhadap yang pertama. Selain itu, istilah interaksi memungkinkan adanya variasi acak dalam respons untuk setiap kelompok perlakuan di setiap periode/unit waktu kalender. Karena efek acak berpusat di sekitar 0, pendekatan ini mengecilkan variasi acak ini ke arah 0. Meskipun dalam tren waktu yang berbeda, pendekatan ini mungkin tidak sepenuhnya menghilangkan bias (karena penyusutan), pendekatan ini diharapkan dapat mengurangi bias dibandingkan dengan model tanpa istilah interaksi.
4 Studi Simulasi
Kami mengevaluasi sifat-sifat metode yang diusulkan dalam Bagian 2 dan 3 dalam studi simulasi dan membahas pengaruh parameter desain tertentu pada tingkat kesalahan tipe I dan daya statistik.
4.1 Desain





| Pengaturan | K | d | λ | Pola tren | Ukuran satuan waktu kalender | Tujuan | Temuan utama dalam pengaturan yang dipertimbangkan | Kondisi untuk kontrol T1E |
|---|---|---|---|---|---|---|---|---|
| 1A | 10 | dk=d·(k−1) ∀k≥1
-d∈[0,500] – dengan kelipatan 25 |
λk=λ0∈[−0.5,0.5] ∀k
– dengan kenaikan 0,125 |
Linier | — | Mengevaluasi model regresi efek tetap dengan penyesuaian periode ( 1 ) | Model efek tetap dengan penyesuaian periode menghasilkan perolehan daya dibandingkan dengan analisis terpisah, asalkan ada beberapa tumpang tindih antara kelompok perawatan. | Tren waktu yang sama dan aditif, pengacakan blok. |
| 1B | 10 | dk=d·(k−1) ∀k≥1
-d=250 |
λk=λ0∈[−0.5,0.5] ∀k
– dengan kenaikan 0,125 |
Linear, bertahap, musiman berbentuk U terbalik | 450 | Mengevaluasi regresi spline ( 3 ) | Regresi spline mengendalikan tingkat kesalahan tipe I jika pola tren waktu cukup halus dan sama di semua lengan. Dalam kasus dengan sedikit atau tidak ada tumpang tindih antara lengan perlakuan, spline mencapai daya yang lebih besar daripada model regresi dengan penyesuaian periode. | Tren waktu yang sama dan aditif, pola tren yang cukup mulus, pengacakan blok. |
| 2A | 4 |
– |
λk=λ0∈[−0.5,0.5] ∀k
– dengan kenaikan 0,125 |
Linear, bertahap, musiman berbentuk U terbalik | [25, 750] dengan kenaikan 25 | Mengevaluasi definisi waktu sebagai interval waktu kalender dalam model efek tetap ( 2 ) | Inflasi tingkat kesalahan Tipe I bergantung pada ukuran unit, dan pola serta kekuatan tren waktu. Kontrol tingkat kesalahan Tipe I yang tepat hanya tercapai jika interval waktu kalender sesuai dengan waktu masuk dan keluar dari kelompok eksperimen dan tren waktu sama di semua kelompok. Unit waktu kalender yang lebih besar menghasilkan peningkatan daya yang lebih besar. | Tren waktu yang sama dan aditif, ukuran satuan waktu kalkulasi yang sesuai, pengacakan blok. |
| 2B | 4 |
– |
– dengan kenaikan 0,125 |
Linear, bertahap, musiman berbentuk U terbalik | 100 | Mengevaluasi model campuran tanpa interaksi ( 4 ), ( 5 ) | Model campuran dengan periode sebagai faktor acak tidak mengendalikan tingkat kesalahan tipe I dalam tren waktu. Inflasi tingkat kesalahan tipe I lebih jelas terlihat dalam kasus tren waktu sedang. | Tingkat kesalahan tipe I tidak terkendali dalam tren waktu positif dan konservatif dalam tren waktu negatif. |
| 3 | 4 |
– |
1) λ1∈[−0.5,0.5]Bahasa Indonesia:
λ0=λ2=λ3=λ4=0 2) λ1=λ2∈[−0.5,0.5]Bahasa Indonesia: λ0=λ3=λ4=0 3) λ1=λ2=λ4∈[−0.5,0.5]Bahasa Indonesia: λ0=λ3=0 4) λ1∈[−0.5,0.5] λ2=2λ1 λ4=3λ1 λ0=λ3=0 5) λk=λ0∈[−0.5,0.5] ∀k – interval dengan kenaikan 0,125 |
Linier | 100 | Mengevaluasi model campuran dengan interaksi ( 6 ), ( 7 ) | Model campuran dengan periode efek tetap dan interaksi antara periode dan perlakuan sebagai efek acak mengurangi inflasi tingkat kesalahan tipe I dalam pengaturan dengan tren waktu yang tidak sama di seluruh lengan dibandingkan dengan model efek tetap dengan penyesuaian periode, tetapi tidak menghilangkannya sepenuhnya. | Tren waktu yang sama dan aditif, ukuran unit waktu kalkulasi yang sesuai, pengacakan blok. Dalam tren waktu yang tidak sama, inflasi T1E lebih kecil daripada model efek tetap ( 1 ). |
4.1.3 Implementasi
Studi simulasi dilakukan menggunakan paket NCC R (Krotka et al. 2023 ), menggunakan versi yang diberi label Release 1.4 di GitHub. Paket tersebut berisi fungsi-fungsi yang mengimplementasikan semua pendekatan analisis yang dipertimbangkan, serta fungsi-fungsi untuk simulasi data dan melakukan studi simulasi (Krotka et al. 2023 ).
4.2 Hasil
Untuk keterbacaan yang lebih baik dan perbandingan yang lebih mudah, kami membatasi rentang sumbu y di semua plot yang menunjukkan daya statistik menjadi [0,7, 1]. Jika daya tidak terlihat untuk beberapa nilai pada sumbu x , daya yang diestimasikan berada di bawah 0,7. Di semua plot yang menunjukkan estimasi tingkat kesalahan tipe I, kami menyertakan garis referensi putus-putus untuk tingkat signifikansi nominal 0,025 dan area abu-abu di sekitar nilai ini yang mewakili interval prediksi 95% dari tingkat kesalahan tipe I yang disimulasikan dengan 10.000 kali simulasi, asalkan tingkat kesalahan tipe I yang sebenarnya adalah 0,025.
4.2.1 Setting 1: Menilai Properti Model Efek Tetap dengan Penyesuaian Periode dan Regresi Spline
Dengan mempertimbangkan uji coba platform dengan 10 kelompok perlakuan eksperimental dan kelompok kontrol bersama, kami menilai karakteristik pengoperasian model efek tetap yang disesuaikan dengan periode dan regresi spline. Secara khusus, kami mengevaluasi efek ukuran sampel yang tumpang tindih dan kekuatan serta pola tren waktu pada tingkat kesalahan tipe I dan daya statistik.
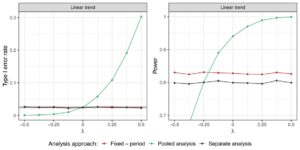
Pengaturan 1A . Gambar 4 menunjukkan dampak kekuatan tren waktu pada karakteristik pengoperasian saat mengevaluasi lengan perawatan 5. Plot analog untuk semua lengan perawatan dapat ditemukan pada Gambar S1 di Informasi Pendukung. Model regresi dan analisis terpisah secara asimtotik mengendalikan rasio kesalahan tipe I, terlepas dari kekuatan tren waktu. Analisis gabungan menyebabkan inflasi kesalahan tipe I jika ada tren waktu positif dan deflasi jika ada tren waktu negatif. Selain itu, model menghasilkan peningkatan daya jika dibandingkan dengan analisis terpisah. Hasil ini sejalan dengan karya sebelumnya (Bofill Roig et al. 2022 ; Lee dan Wason 2020 ), di mana model regresi diselidiki untuk uji coba dengan dua lengan eksperimen saja.

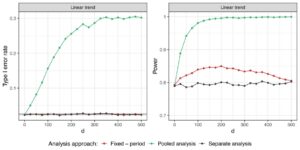
Gambar S3 dalam Informasi Pendukung mengilustrasikan bagaimana tingkat kesalahan tipe I dan daya untuk perbandingan perlakuan–kontrol individual bergantung pada urutan entri dalam uji coba platform. Kami mengamati bahwa daya model regresi meningkat untuk kelompok yang ditambahkan ke uji coba selanjutnya. Hal ini disebabkan oleh ukuran sampel data NCC yang lebih besar. Di sisi lain, hal ini juga menyebabkan inflasi kesalahan tipe I yang lebih tinggi dengan analisis gabungan, sementara model regresi mengendalikan kesalahan tipe I untuk semua perbandingan perlakuan–kontrol.
Singkatnya, model regresi efek tetap dengan penyesuaian periode menawarkan kinerja yang unggul dalam hal kekuatan statistik dalam uji coba di mana kelompok perlakuan masuk secara bertahap tetapi tumpang tindih untuk beberapa waktu. Kelompok perlakuan yang ditambahkan ke uji coba kemudian memiliki keuntungan berupa lebih banyak data NCC yang tersedia untuk perbandingan perlakuan-kontrol, sehingga ada kemungkinan yang lebih tinggi untuk mengidentifikasi kelompok percobaan yang berkhasiat.
Pengaturan 1B . Kinerja regresi spline dievaluasi di bawah berbagai tumpang tindih antara lengan perlakuan, serta tren waktu dari berbagai pola dan kekuatan. Kami juga memvariasikan derajat B-spline dalam simulasi, dengan mempertimbangkan spline linier, kuadrat, dan kubik. Namun, karena perbedaan dalam karakteristik operasi yang dihasilkan hanya marjinal, di sini kami hanya menyajikan hasil untuk regresi spline kubik. Hasil untuk spline linier dan kuadrat dapat ditemukan dalam Gambar Informasi Pendukung S4 dan S5 . Titik simpul ditempatkan di awal setiap periode atau setiap interval waktu kalender.
Tingkat kesalahan tipe I dan daya model yang dievaluasi di bawah skenario yang dipertimbangkan saat membandingkan lengan perawatan 5 dengan kontrol disajikan dalam Gambar 6 dan 7. Plot analog untuk lengan eksperimen lainnya diberikan dalam Gambar S6 dan S7 dalam Informasi Pendukung. Jika pola tren waktu diberikan oleh fungsi yang cukup halus, regresi spline mempertahankan tingkat kesalahan tipe I. Namun, dalam kasus tren waktu bertahap, kami mengamati inflasi dalam tingkat kesalahan tipe I. Ini karena regresi spline memperkirakan efek waktu dengan fungsi halus, yang terdiri dari beberapa fungsi polinomial yang digabungkan bersama dalam simpul. Ini bukan pendekatan yang valid jika ada lonjakan tiba-tiba dalam tren waktu. Model regresi mempertahankan tingkat kesalahan tipe I di bawah pola tren waktu dan kekuatan yang sewenang-wenang. Perhatikan bahwa pendekatan terpisah memiliki tingkat kesalahan tipe I tepat di bawah 2,5% untuk tren waktu yang kuat di bawah pola tren musiman dan khususnya di bawah pola tren bertahap, karena yang ini memiliki nilai yang lebih kuat daripada bentuk lainnya. Alasannya adalah bahwa pengacakan blok digunakan untuk menetapkan pasien ke lengan aktif. Dalam kasus tren waktu yang sangat kuat, mengabaikan blok dalam analisis menghasilkan pengujian yang konservatif, karena varians efek perlakuan ditaksir terlalu tinggi. Hal ini menyebabkan deflasi dalam tingkat kesalahan tipe I, yang semakin kuat seiring tren waktu yang semakin ekstrem (Matts dan Lachin 1988 ).

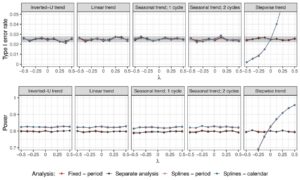

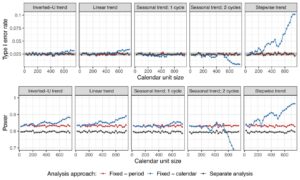
Dalam kasus yang dipertimbangkan di sini, dengan unit waktu kalender yang dipilih sedemikian rupa sehingga kelompok perlakuan dapat masuk atau keluar dalam interval, penyesuaian untuk interval ini mengarah pada pengumpulan data uji coba dengan skema pengacakan yang berbeda, karena jumlah kelompok aktif berubah. Hilangnya kontrol tingkat kesalahan tipe I, yang dapat diamati khususnya untuk ukuran unit kalender yang lebih besar, kemudian disebabkan oleh efek pengumpulan data yang lebih besar. Dalam uji coba dengan perubahan mendadak dalam tren waktu (seperti pola tren bertahap yang dipertimbangkan), inflasi kesalahan tipe I untuk pengumpulan naif bahkan lebih jelas.
Bergantung pada ukuran unit, model dengan penyesuaian waktu kalender dapat menghasilkan peningkatan daya dibandingkan dengan penyesuaian periode. Secara khusus, dalam uji coba di mana respons pasien tidak berubah secara substansial seiring waktu (misalnya, uji coba dengan pola tren waktu linear atau U terbalik dan
relatif terhadap efek perlakuan), perolehan daya dapat dicapai dengan mempertimbangkan satuan waktu kalender yang lebih besar daripada periode, sambil tetap mempertahankan kendali tingkat kesalahan tipe I (lihat Gambar 8 ).
Karena pilihan panjang interval waktu kalender menentukan hasil trade-off antara tingkat kesalahan tipe I dan tipe II dan perlu dinilai secara hati-hati dalam simulasi saat merencanakan uji coba platform. Jika lengan eksperimental diizinkan untuk masuk dan meninggalkan uji coba hanya pada awal unit waktu kalender, kontrol tingkat kesalahan tipe I akan dipastikan terlepas dari pola dan kekuatan tren waktu, karena setiap perubahan dalam desain pengacakan akan disesuaikan. Namun, di bawah pengaturan ini, model dengan penyesuaian waktu kalender tidak menawarkan keuntungan apa pun dalam daya dibandingkan dengan penyesuaian periode. Kami tidak mempertimbangkan desain ini dalam simulasi kami, karena kami bertujuan untuk mengevaluasi kasus umum dengan ukuran unit yang sewenang-wenang.
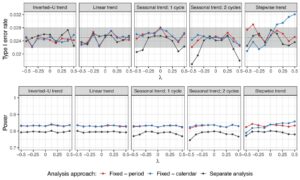
Pengaturan 2B . Demikian pula, untuk evaluasi model campuran tanpa interaksi, kami fokus pada evaluasi kelompok perlakuan 3, mempertimbangkan pola tren waktu dan kekuatan yang bervariasi, dan menyajikan tingkat kesalahan tipe I dan daya yang dihasilkan pada Gambar 10. Gambar S10 dalam Informasi Pendukung menunjukkan hasil yang sesuai untuk kelompok perlakuan lainnya.
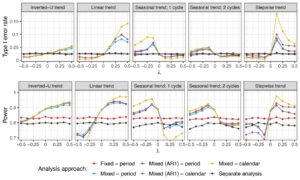



Seperti yang ditunjukkan dalam Bofill Roig et al. ( 2022 ), tingkat kesalahan tipe I dikontrol untuk tren waktu yang berbeda di seluruh kelompok ketika istilah interaksi disertakan sebagai efek tetap. Namun, model seperti itu tidak menawarkan peningkatan daya dibandingkan dengan analisis terpisah.
4.3 Ringkasan Hasil Utama
Di bawah ini kami merangkum kelebihan dan keterbatasan metode yang dipertimbangkan dan hasil utama dari studi simulasi dan menjelaskan pengaruh parameter desain tertentu.
Regresi efek tetap dengan penyesuaian periode: Model efek tetap dengan penyesuaian periode mempertahankan tingkat kesalahan tipe I dan menghasilkan peningkatan daya dibandingkan dengan analisis terpisah jika terjadi tren waktu yang sama antara lengan yang bersifat aditif pada skala model, untuk pola tren waktu yang berubah-ubah. Namun, tumpang tindih waktu tertentu antara lengan perlakuan eksperimental diperlukan untuk mencapai peningkatan daya. Jumlah peningkatan daya bergantung pada ukuran data NCC dan jumlah tumpang tindih.
Regresi spline dengan penyesuaian periode: Regresi spline mempertahankan tingkat kesalahan tipe I dalam skenario di mana pola tren waktu cukup halus dan sama di semua lengan. Selain itu, hal ini dapat menyebabkan peningkatan daya dibandingkan dengan model efek tetap dengan penyesuaian periode, terutama dalam kasus dengan sedikit atau tidak ada tumpang tindih antara lengan perlakuan eksperimental.
Regresi efek campuran dengan penyesuaian periode: Model campuran yang periodenya dimodelkan sebagai efek acak tidak mengendalikan rasio kesalahan tipe I dengan adanya tren waktu. Inflasi lebih jelas terlihat dalam kasus dengan tren waktu sedang dibandingkan dengan kasus dengan tren waktu yang kuat. Model campuran dengan periode efek tetap dan efek acak untuk interaksi antara perlakuan dan periode mengendalikan rasio kesalahan tipe I dalam uji coba dengan tren waktu yang sama, dan mengurangi inflasi dalam pengaturan dengan tren waktu yang tidak sama, tetapi tidak menghilangkannya sepenuhnya. Dalam kasus dengan tren waktu yang tidak sama, rasio kesalahan tipe I dikendalikan oleh model regresi yang mencakup interaksi antara perlakuan dan waktu sebagai efek tetap (Bofill Roig et al. 2022 ). Namun, metode ini tidak menawarkan peningkatan daya dibandingkan dengan analisis terpisah.
Penyesuaian periode versus waktu kalender: Selain penyesuaian periode yang diteliti dalam karya-karya sebelumnya, kami mempertimbangkan untuk menyesuaikan unit waktu kalender yang, tidak seperti periode, independen dari kemajuan uji coba. Dengan menggunakan penyesuaian ini, jumlah tingkat faktor dalam model regresi yang dihasilkan, atau jumlah simpul dalam untuk fungsi spline, dapat dikontrol oleh parameter desain tambahan.(panjang satuan waktu kalender). Bergantung pada pola dan kekuatan tren waktu, penyesuaian untuk satuan yang lebih besar daripada yang diberikan oleh periode dapat menghasilkan peningkatan daya, sambil tetap mengendalikan rasio kesalahan tipe I. Kontrol rasio kesalahan tipe I akan dipastikan dalam kasus di mana lengan eksperimental baru hanya masuk dan meninggalkan uji coba pada awal satuan waktu kalender, tetapi pengaturan ini tidak akan menghasilkan peningkatan daya yang substansial dibandingkan dengan penyesuaian periode. Perhatikan juga bahwa interval waktu kalender terakhir dipotong pada titik waktu saat lengan yang dievaluasi meninggalkan platform untuk menghindari penyertaan data mendatang ke analisis, yang mungkin tidak tersedia pada saat menilai lengan yang diberikan.
Tumpang tindih antara lengan eksperimen: Kami menunjukkan bahwa tumpang tindih tertentu antara lengan eksperimen diperlukan untuk model regresi efek tetap dengan penyesuaian periode untuk mencapai peningkatan daya dibandingkan dengan analisis terpisah. Namun, hal ini tidak diperlukan oleh regresi spline, yang menggunakan penyesuaian waktu berkelanjutan, bukan kategoris dan mengarah pada peningkatan daya bahkan dalam kasus tanpa tumpang tindih, yaitu, jika hanya satu lengan eksperimen yang aktif pada waktu tertentu.
5 Studi Kasus
Kami mencontohkan penggunaan metode yang diusulkan dalam studi kasus berdasarkan uji klinis di dunia nyata. Studi ini meninjau kembali data nyata dari uji klinis untuk PSP (Höglinger et al. 2021 ) dan menganalisis pengukuran dasar, sehingga menggambarkan penggunaan pendekatan pemodelan dalam situasi di mana hipotesis nol diasumsikan berlaku.
Selain itu, dalam Informasi Pendukung (Bagian D ), kami menyajikan studi kasus kedua yang meniru desain uji coba platform FLAIR untuk leukemia limfositik kronis (Hillmen et al. 2023 ; Howard et al. 2021 ; Munir et al. 2024 ) menggunakan data simulasi. Studi kasus ini menggabungkan elemen desain tertentu dari uji coba FLAIR dan menunjukkan penerapan metode dalam skenario yang melibatkan dua opsi pengobatan yang mujarab.
Kami menganalisis ulang data dari uji coba ABBV-8E12 (Höglinger et al. 2021 ) untuk PSP, kelainan neurodegeneratif langka yang memengaruhi keseimbangan, gerakan tubuh, penglihatan, dan bicara, yang akhirnya mengakibatkan kematian. Studi ABBV-8E12 mengevaluasi keamanan dan kemanjuran berbagai dosis (2000 mg—di sini dilambangkan sebagai kelompok 1; dan 4000 mg—dilambangkan sebagai kelompok 2) dari pengobatan eksperimental Tilavonemab dalam uji coba kelompok paralel acak, menggunakan plasebo sebagai kelompok kontrol umum. Uji coba ini merekrut pasien selama periode sekitar 2 tahun, dari Januari 2017 hingga Maret 2019. Ketika meninjau kembali data ini, kami mempertimbangkan Progressive Supranuclear Palsy Rating Scale (PSPRS) sebagai titik akhir, skor jumlah yang menjumlahkan nilai untuk 28 item berbeda, yang mengukur perkembangan penyakit di berbagai domain (nilai yang lebih rendah dari skor ini menunjukkan hasil yang lebih baik) (Golbe dan Ohman-Strickland 2007 ). Untuk menunjukkan dampak potensial dari tren waktu di bawah hipotesis nol, untuk tujuan ilustrasi, kami membandingkan pengukuran dasar dari skor jumlah antara kelompok perlakuan dan kontrol (bukan perubahan dari dasar seperti dalam uji coba asli). Untuk pengukuran dasar, kami tahu bahwa karena pengacakan tidak ada efek pengobatan dibandingkan dengan plasebo untuk kedua lengan, sehingga semua efek pengobatan yang diamati disebabkan oleh bias atau kesalahan pengambilan sampel. Kami selanjutnya menunjukkan penggunaan model yang diusulkan pada data ini.
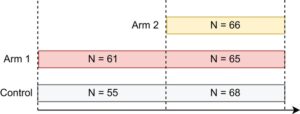
Bahasa Indonesia: Untuk meniru uji coba platform dua periode, kami memodifikasi data uji coba multilengan asli dan berasumsi bahwa lengan eksperimen kedua (4000 mg Tilavonemab) memasuki uji coba yang sedang berlangsung di titik waktu berikutnya. Oleh karena itu, kami menetapkan batas untuk periode tersebut (yaitu, titik waktu di mana lengan pengobatan 2 memasuki platform) ke 1.6.2018 dan mengecualikan pengamatan dari pasien yang dialokasikan ke lengan 2 sebelum tanggal batas ini dari analisis. Set data yang dihasilkan terdiri dari 315 pasien, dengan ukuran sampel 123, 126, dan 66 untuk lengan plasebo, dan lengan pengobatan 1 dan 2, masing-masing. Ukuran sampel per lengan dan periode disajikan dalam Gambar 12. Untuk pendekatan yang disesuaikan dengan waktu kalender, kami menggunakan panjang unit 90 hari, yang membagi uji coba menjadi sembilan unit waktu kalender, yang masing-masing sesuai dengan sekitar 3 bulan. Perlu dicatat bahwa karena perekrutan pasien tidak seragam, jumlah pasien di setiap unit berbeda, mulai dari 4 di unit pertama hingga 96 di unit kedelapan. Gambar 13 memvisualisasikan data yang dipertimbangkan, yang menunjukkan pembagian ke dalam periode (garis putus-putus merah) dan unit waktu kalender (garis putus-putus abu-abu).
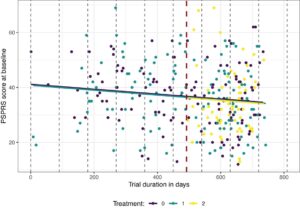
Pertama, kami menyelidiki keberadaan tren waktu yang mungkin dalam data uji coba yang dimodifikasi dengan menyesuaikan model linier dengan hasil utama, menggunakan perawatan sebagai kategoris, dan hari sejak perekrutan pasien pertama sebagai kovariat kontinu. Nilai yang disesuaikan dari model ini disertakan sebagai garis padat pada Gambar 13. Model menunjukkan tren waktu negatif yang signifikan ( p = 0,032), yang juga terlihat pada gambar. Oleh karena itu, pada awalnya, uji coba merekrut pasien dengan stadium penyakit yang lebih parah, sementara peserta yang direkrut kemudian rata-rata memiliki stadium PSP yang lebih ringan.
Selanjutnya, kami menganalisis kumpulan data menggunakan pendekatan pemodelan yang diusulkan, serta analisis terpisah dan gabungan, dan membandingkan efek pengobatan yang diestimasikan, kesalahan standarnya, dan nilai- p . Dalam kasus model campuran, kami hanya mempertimbangkan penyesuaian waktu kalender, karena uji coba yang dianalisis hanya terdiri dari dua periode, yang akan mengarah pada estimasi efek acak yang sangat tidak stabil jika terjadi penyesuaian periode. Kami fokus pada evaluasi kemanjuran lengan eksperimen kedua terhadap kontrol, karena lengan ini memiliki data NCC yang tersedia. Tabel 2 merangkum hasil yang diperoleh. Karena respons yang dipertimbangkan diukur pada tanggal awal dalam uji coba acak, kami dapat mengasumsikan bahwa hipotesis nol berlaku, sehingga efek pengobatan yang mendasarinya adalah 0 untuk kedua lengan. Kami mengevaluasi hipotesis nol ini (
) terhadap alternatif dua sisi (
). Tidak ada pendekatan analisis yang menolak hipotesis nol. Estimasi paling akurat dari efek pengobatan (−0,012) disediakan oleh model efek tetap yang disesuaikan dengan periode, diikuti oleh model efek tetap dengan penyesuaian waktu kalender (−0,068). Model-model ini juga menghasilkan nilai- p tertinggi terhadap hipotesis nol ( masing-masing p = 0,995 dan p = 0,971). Estimasi terdekat kedua disediakan oleh regresi spline, yang menghasilkan efek estimasi sebesar 0,178 dan 0,624 untuk penyesuaian periode dan waktu kalender, masing-masing. Di kedua kelas model (model efek tetap dan regresi spline), penyesuaian periode mengarah pada estimasi efek yang lebih baik daripada penyesuaian waktu kalender. Kesalahan standar estimasi sebanding untuk semua model yang dipertimbangkan, berkisar dari 1,822 (model campuran dengan efek acak autokorelasi dan penyesuaian waktu kalender) hingga 1,900 (model efek tetap dengan penyesuaian waktu kalender). Kita juga dapat mengamati bahwa semua pendekatan pemodelan menghasilkan estimasi yang lebih dekat dengan efek sebenarnya daripada analisis gabungan, yang memperkenalkan bias yang cukup besar pada estimasi efek (−1.7030) dan juga memberikan nilai p terendah ( p = 0,336).
| Pendekatan analisis | Pengaturan | Perkiraan dampak | Kesalahan standar | nilai p |
|---|---|---|---|---|
| Model efek tetap | Periode | -0,012 | 1.896 | 0,995 |
| Satuan waktu kalender | -0,068 | 1.900 | 0,971 tahun | |
| Model campuran | Satuan waktu kalender | -0,903 | 1.833 | 0.623 |
| Model campuran (AR1) | Satuan waktu kalender | -0,973 | 1.822 | 0,594 tahun |
| Regresi spline | Periode | 0,178 | 1.885 | 0.924 |
| Satuan waktu kalender | 0.624 | 1.879 | 0.740 | |
| Analisis gabungan | — | -1.703 | 1.766 | 0,336 tahun |
| Analisis terpisah | — | -0,410 | 2.032 | 0.840 |
Dalam uji coba ABBV-8E12, titik akhir primer adalah perubahan dari skor PSPRS awal setelah 52 minggu. Kami juga menyelidiki tren waktu potensial untuk titik akhir ini, tetapi tidak mengamati pergeseran substansial dalam hasil ini selama uji coba (data tidak ditampilkan). Oleh karena itu, data ini menunjukkan bahwa tren waktu tidak akan menimbulkan masalah dalam uji coba khusus ini, dan fakta bahwa pasien dengan stadium PSP yang lebih ringan direkrut di kemudian hari dalam uji coba diperhitungkan dengan menyesuaikan respons awal. Untuk penilaian efisiensi pilihan lain untuk titik akhir primer, lihat Yousefi et al. ( 2024 ).
6 Diskusi
Penggunaan NCC dalam analisis uji coba platform telah menjadi subjek diskusi dan penelitian metodologis yang intensif selama beberapa tahun terakhir. Dalam karya ini, kami memperluas metode frekuentis yang tersedia saat ini dan mengusulkan pendekatan berbasis model yang baru untuk memanfaatkan NCC untuk perbandingan perlakuan-kontrol individual. Kami memperkenalkan definisi alternatif dari kovariat waktu dalam model frekuentis, di mana durasi uji coba dibagi menjadi interval waktu kalender dengan panjang yang sama. Ini analog dengan kelompok waktu yang dipertimbangkan dalam pendekatan “Mesin Waktu” Bayesian (Saville et al. 2022 ). Selain itu, kami mempertimbangkan cara yang lebih fleksibel untuk memodelkan tren waktu. Secara khusus, kami mengusulkan untuk menambahkan kovariat waktu sebagai efek acak dalam model campuran linier. Dalam model ini, kami juga memungkinkan autokorelasi antara efek acak untuk memperhitungkan ketergantungan antara interval waktu yang lebih dekat. Lebih jauh, kami menggunakan B-splines untuk memodelkan waktu dengan fungsi polinomial dalam regresi spline. Di sini kami mempertimbangkan dua opsi penempatan simpul dalam—baik menurut periode dalam uji coba atau menurut interval waktu kalender. Untuk melonggarkan asumsi tren waktu yang sama yang penting untuk semua metode yang dipertimbangkan sebelumnya, kami mengusulkan perluasan pendekatan pemodelan, di mana kami memasukkan perlakuan dan waktu sebagai efek tetap dan interaksi di antara keduanya sebagai efek acak.
Kami mengevaluasi kinerja metode yang diusulkan dalam hal tingkat kesalahan tipe I dan daya statistik dalam studi simulasi, dengan mempertimbangkan berbagai skenario. Kami menentukan dalam kondisi apa model efek tetap yang disesuaikan untuk periode menghasilkan peningkatan daya dibandingkan dengan analisis terpisah. Selain itu, kami menunjukkan bahwa penyesuaian waktu kalender dalam model efek tetap dapat, dalam beberapa skenario, menghasilkan peningkatan daya dibandingkan dengan penyesuaian periode sambil tetap mengendalikan tingkat kesalahan tipe I. Dalam skenario yang dipertimbangkan, model campuran tanpa interaksi tidak cocok untuk mengevaluasi kemanjuran lengan pengobatan yang memasuki akhir dengan adanya tren waktu, karena model tersebut tidak mempertahankan tingkat kesalahan tipe I. Lee dan Wason ( 2020 ) dan Bofill Roig et al. ( 2022 ) menyelidiki model regresi linier yang memasukkan waktu sebagai variabel kontinu, bukan variabel kategoris. Ditunjukkan bahwa model ini hanya mengendalikan tingkat kesalahan tipe I jika tren waktu yang mendasarinya memiliki pola linier. Regresi spline dapat dilihat sebagai generalisasi dari model ini, yang menyesuaikan satu fungsi polinomial untuk setiap periode atau interval waktu kalender, daripada satu fungsi linear untuk seluruh percobaan, untuk menyesuaikan waktu. Kami menunjukkan melalui simulasi bahwa pemodelan waktu melalui fungsi spline mengontrol tingkat kesalahan tipe I untuk semua skenario yang dipertimbangkan dengan tren waktu yang cukup mulus. Metode lain yang menggunakan penghalusan lintas waktu untuk memperkirakan efek perlakuan adalah Bayesian Time Machine (Saville et al. 2022 ). Namun, kinerja Time Machine sangat bergantung pada pilihan distribusi sebelumnya. Selain itu, ia memerlukan spesifikasi interval waktu kalender. Regresi spline dengan penyesuaian periode, di mana penempatan simpul diberikan oleh periode, di sisi lain, hanya memerlukan pilihan derajat fungsi polinomial, dengan spline kubik menjadi opsi default yang sesuai, karena mereka memastikan kontrol tingkat kesalahan tipe I bahkan dalam kasus dengan pola tren waktu yang kompleks. Lebih jauh, ditunjukkan bahwa model dengan periode faktor tetap yang juga mencakup istilah untuk interaksi antara perlakuan dan waktu sebagai efek acak, dapat meningkatkan ketahanan dan mengurangi inflasi tingkat kesalahan tipe I dibandingkan dengan model tanpa interaksi ini, jika tren waktu tidak sama di seluruh lengan. Pendekatan analisis yang diusulkan hanya berfokus pada uji coba dengan titik akhir berkelanjutan. Perluasan metode yang disajikan ke jenis titik akhir lainnya, seperti titik akhir biner atau waktu-ke-peristiwa, masih terbuka untuk penelitian di masa mendatang.
NCC memiliki beberapa karakteristik yang sama dengan kontrol historis, karena keduanya merujuk pada data yang dikumpulkan sebelum data pada perawatan yang diteliti, sehingga keduanya dapat menimbulkan bias dalam estimasi dan meningkatkan rasio kesalahan tipe I jika disertakan dalam analisis (Burger et al. 2021 ; Kopp-Schneider et al. 2020 ). Namun, dibandingkan dengan kontrol historis, NCC terdiri dari pasien yang telah menjadi bagian dari kerangka uji yang sama dengan pasien yang dialokasikan untuk perawatan yang diselidiki. Oleh karena itu, mereka biasanya memiliki kriteria inklusi dan eksklusi serta prosedur penilaian titik akhir yang sama (Sridhara et al. 2022 ). Metode untuk menggabungkan kontrol historis dalam uji klinis acak telah banyak dibahas dalam beberapa tahun terakhir, dan dapat digunakan secara analogis dalam konteks uji platform untuk menggabungkan data NCC (Bofill Roig et al. 2023 ). Metode frekuentis mencakup misalnya pendekatan “uji-lalu-kumpulkan”, di mana analisis terpisah atau gabungan dilakukan berdasarkan uji frekuentis yang menilai kesetaraan CC dan data historis (Viele et al. 2014 ); pengumpulan dinamis, yang menetapkan parameter bobot pada data historis untuk mengendalikan proporsinya dalam analisis (Jiao et al. 2019 ); atau metode skor kecenderungan yang dapat digunakan untuk menyesuaikan ketidakseimbangan dalam kovariat dasar antara historis dan CC (Schmidli et al. 2020 ). Pendekatan Bayesian mencakup metode prior daya, yang menurunkan bobot informasi historis dengan memperkenalkan parameter daya ke fungsi kemungkinannya (Banbeta et al. 2019 ); prior daya sepadan, perluasan dari pendekatan prior daya yang secara langsung meparameterkan keselarasan data historis dan CC (Hobbs et al. 2011 ); dan pendekatan meta-analitik-prediktif (MAP) sebelumnya, yang menggunakan informasi historis untuk memperoleh distribusi MAP sebelumnya untuk data CC (Schmidli et al. 2014 ; Weber et al. 2021 ). Metode Bayesian lainnya, seperti peminjaman dinamis, juga diusulkan untuk menggabungkan data eksternal ke dalam analisis uji klinis guna memperoleh informasi lebih lanjut untuk pengambilan keputusan (Di Stefano et al. 2023 ; Edwards et al. 2024). Akan tetapi, berbeda dengan pendekatan pemodelan untuk menggabungkan data NCC, metode ini tidak secara langsung menyesuaikan tren waktu, tetapi justru menurunkan bobot informasi historis untuk memperbaiki bias akibat heterogenitas dalam data. Oleh karena itu, metode ini tetap menimbulkan beberapa bias jika tren waktu hadir. Sebaliknya, pendekatan berbasis model untuk menggabungkan NCC menghasilkan estimasi yang tidak bias asalkan asumsi model terpenuhi. Tinjauan terperinci tentang metode yang dibahas dalam konteks kontrol historis, non-konkuren, dan/atau eksternal disediakan dalam tinjauan cakupan oleh Bofill Roig et al. ( 2023 ).
Baru-baru ini, Marschner dan Schou ( 2024 ) mempertimbangkan penggunaan NCC dalam uji klinis dengan kriteria kelayakan yang bervariasi di seluruh kelompok. Dalam kasus ini, penggunaan subjek CC yang tidak memenuhi kriteria kelayakan kelompok pengobatan yang sesuai juga dapat menimbulkan bias dalam perbandingan pengobatan-kontrol. Mereka merujuk ke NCC untuk kelompok percobaan tertentu sebagai pasien yang tidak termasuk dalam kohort acak serentak yang sama. Kohort acak serentak hanya terdiri dari pasien yang memenuhi syarat untuk rangkaian pengobatan yang sama dan diacak menggunakan metode alokasi yang sama (Marschner dan Schou 2024 ). Dalam makalah ini, kami berasumsi bahwa untuk semua kelompok, kriteria kelayakan yang sama berlaku. Jika tidak demikian halnya, seseorang dapat memasukkan model yang diusulkan ke dalam subkelompok pasien yang memenuhi kriteria kelayakan kelompok pengobatan yang diuji.
Selain risiko bias karena tren waktu, mungkin ada sumber bias lain saat menggunakan NCC. Karena uji coba platform dirancang untuk berjalan selama beberapa tahun, hasil dari lengan yang lengkap dapat dipublikasikan sebelum seluruh uji coba berakhir. Ini dapat memengaruhi spesifikasi metode analisis dan dengan demikian integritas uji coba untuk lengan yang masih aktif atau sedang dipertimbangkan untuk memasuki platform (Koenig et al. 2024 ). Misalnya, ini dapat memengaruhi kemauan pemilik intervensi untuk memasukkan lengan perawatan baru ke dalam platform, membuat uji coba platform dengan kontrol dengan hasil rendah acak lebih menarik untuk diikuti. Sebaliknya, uji coba platform dengan hasil tinggi acak dapat menjadi penghalang bagi pemilik intervensi.
Sementara analisis menggunakan CC saja masih dianggap sebagai pendekatan yang lebih disukai, dalam keadaan tertentu, seperti uji coba untuk penyakit langka, penggunaan NCC dapat berharga (Bofill Roig et al. 2023 ; US Food and Drug Administration 2023 ). Dalam kasus seperti itu, metode untuk mengatasi potensi bias karena tren waktu harus digunakan (US Food and Drug Administration 2023 ). Model yang diusulkan dalam karya ini bertujuan untuk mengatasi tren waktu ini dan dapat meningkatkan presisi estimator efek pengobatan, sambil mengurangi bias yang dapat muncul karena perubahan temporal. Namun, mengingat kinerja metode analisis bergantung pada banyak faktor, implikasi dari penyertaan NCC dan perilaku metode yang dipertimbangkan harus diselidiki berdasarkan kasus per kasus saat merencanakan uji coba platform tertentu.