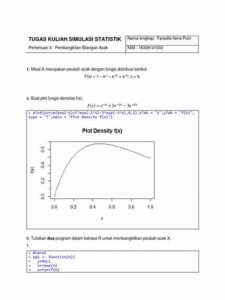
Abstrak
Kami menunjukkan bahwa permukaan K3 dalam karakteristik 2 dapat menerima kumpulanpersamaan matematikakurva rasional halus terpisah yang jumlahnya habis dibagi 2 dalam grup Picard, untuk setiappersamaan matematikaLebih tepatnya, semua nilai terjadi pada permukaan K3 supersingular, dengan pengecualian hanya pada invarian Artin 1 dan 10, sedangkan pada permukaan K3 dengan tinggi terbatas, hanyapersamaan matematikaadalah mungkin.

1. PENDAHULUAN
Penutup ganda memainkan peran kunci dalam geometri aljabar. Pentingnya penutup ganda untuk permukaan aljabar dibuktikan oleh permukaan Kummer dan oleh tempat sentral yang mereka ambil dalam klasifikasi Enriques–Kodaira, terutama dalam dimensi nol Kodaira. Interaksi penutup ganda dan pembagian-2 dari pembagi efektif dieksplorasi dengan baik, lihat, misalnya, [ 26 ] dan, dalam generalitas yang jauh lebih besar, [ 3 , Bagian 0.2]. Dalam makalah ini, kami fokus pada masalah pembagian-2 untuk permukaan K3 dalam karakteristik 2 dan membuktikan analog dari hasil klasik Nikulin, lihat Teorema 1.1 .

Membiarkanpersamaan matematikamenjadi bidang karakteristik aljabar tertutuppersamaan matematika, dan biarkanpersamaan matematikamenjadi permukaan K3 yang didefinisikan di ataspersamaan matematika. Membiarkanpersamaan matematika(persamaan matematikamenjadi terpisah-pisahpersamaan matematika-kurva (yaitu, kurva rasional non-singular) padapersamaan matematikaJika pembagipersamaan matematikadapat dibagi 2 dipersamaan matematika, maka hal ini akan menyebabkan lapisan gandapersamaan matematika, dan kita mendapatkan permukaan baru. Faktanya, kita sering mengalami situasi seperti itu. Jika terjadipersamaan matematikaNikulin [ 22 ] menunjukkan bahwa jikapersamaan matematikadapat dibagi 2 dipersamaan matematikaBahasa Indonesia:persamaan matematikasama denganpersamaan matematikaataupersamaan matematikaDalam kasuspersamaan matematika, dia menunjukkan bahwa dengan menggunakanpersamaan matematikakita bisa membuat penutuppersamaan matematikaderajat 2 daripersamaan matematikayang merupakan permukaan abelian. Dalam kasus ini,persamaan matematikaadalah permukaan Kummer yang terkait dengan permukaan abelianpersamaan matematika(lih. Nikulin [ 22 , Teorema 1]), yaitu,persamaan matematikaadalah resolusi minimal dari permukaan hasil bagipersamaan matematikadengan inversipersamaan matematikadaripersamaan matematikaDanpersamaan matematikaadalah kurva luar biasa di atas enam belas nodepersamaan matematikaHasil ini juga berlaku pada karakteristikpersamaan matematika(lih. Shepherd-Barron [ 30 , Catatan 3.3 (iii)], Matsumoto [ 20 , Proposisi 4.7]). Dalam kasus inipersamaan matematika, dengan menggunakanpersamaan matematika, kita mendapatkan permukaan K3persamaan matematikadengan automorfisme simplektikpersamaan matematikadari orde 2 sehinggapersamaan matematikaadalah resolusi minimal dari permukaan hasil bagipersamaan matematikaDanpersamaan matematikaadalah kurva luar biasa di atas delapan simpulpersamaan matematika(Nikulin [ 24 ]).