ABSTRAK
Pada awal uji klinis fase III, ada optimisme yang besar. Bagaimanapun, hasil uji klinis fase II menggembirakan. Saat itu, data awal dari uji klinis fase III menunjukkan tren yang salah, tetapi masih ada peluang bagi tren tersebut untuk berbalik dan menjadi signifikan secara statistik pada akhirnya. Pada titik manakah optimisme berubah menjadi penyangkalan realitas? Bagaimana kita memutuskan kapan uji klinis itu sia-sia? Apa arti kesia-siaan? Tutorial ini mengulas berbagai konsep dan alat untuk mengevaluasi kesia-siaan, termasuk daya kondisional dan prediktif, daya kondisional terbalik, plot interval terprediksi, daya tak bersyarat yang direvisi, dan fungsi pengeluaran beta.
1 Pendahuluan
Uji coba terkontrol acak adalah tingkat bukti medis tertinggi, tetapi bisa salah dalam banyak hal: Rekrutmen bisa buruk, peserta mungkin merasa terbebani oleh prosedur uji coba dan putus asa, tingkat kejadian mungkin telah ditaksir terlalu tinggi, atau kepatuhan pengobatan mungkin buruk. Akibatnya, pertanyaan uji coba asli tidak dapat dijawab dengan kekuatan yang wajar. Faktor-faktor seperti rekrutmen rendah, putus asa tinggi, kurangnya kepatuhan, dan sebagainya, menyebabkan kesia-siaan operasional , ketidakmampuan untuk menentukan apakah suatu intervensi berhasil. Misalnya, peneliti dalam uji coba ACTIV-4B [ 1 ] berencana untuk mengevaluasi efek terapi antikoagulan dan antiplatelet di antara pasien rawat jalan COVID-19 yang simtomatik dan stabil secara klinis. Mereka mengantisipasi tingkat kejadian kontrol antara 4% dan 8% untuk titik akhir primer komposit mereka berupa mortalitas, tromboemboli vena/arteri simtomatik, infark miokard, stroke, atau rawat inap karena penyebab kardiovaskular atau paru. Setelah 558 pasien memulai pengobatan, hanya lima pasien di antara keempat kelompok yang mengalami titik akhir primer. Jelas bahwa jumlah akhir kejadian tidak akan menghasilkan kekuatan yang cukup untuk membuat kesimpulan yang dapat diandalkan, dan persidangan dihentikan.
Alternatifnya, pengobatan mungkin jauh kurang efektif daripada yang diperkirakan sebelumnya. Ini adalah jenis kesia-siaan yang sangat berbeda karena pertanyaannya dapat dijawab dengan andal, dan jawabannya adalah bahwa intervensi tidak berhasil. Ini adalah kasus uji coba vaksin HIV AIDSVAX pada 5108 pria yang berhubungan seks dengan pria dan 309 wanita yang berisiko tinggi tertular HIV [ 2 ]. Hanya ada 6% kemanjuran vaksin. Dalam beberapa kasus, seperti ketika suatu pengobatan sudah digunakan meskipun belum ada uji coba acak yang menunjukkan kemanjuran pada titik akhir klinis yang penting, seseorang mungkin ingin melanjutkan uji coba untuk menunjukkan bahwa pengobatan tersebut tidak berhasil. Misalnya, hanya bukti kuat dari Uji Coba Penekan Aritmia Jantung [ 3 ] yang dapat meyakinkan dokter bahwa menekan aritmia jantung pada pasien dengan serangan jantung sebelumnya menggunakan golongan obat tertentu berbahaya.
Dua pertanyaan harus dipertimbangkan ketika mencoba memutuskan apakah akan menghentikan uji coba karena sia-sia: (1) Apakah hasil nol mungkin terjadi? (2) Apakah hasil nol masih bermakna? Yang kami maksud dengan “hasil nol” adalah hasil yang tidak signifikan secara statistik pada tingkat kesalahan tipe I yang sesuai. Jika jawaban untuk pertanyaan pertama adalah tidak, maka uji coba tersebut kemungkinan akan memiliki hasil yang signifikan secara statistik, dan tidak ada alasan untuk berhenti karena sia-sia. Jika jawaban untuk pertanyaan pertama adalah ya, maka pertanyaan kedua mungkin ikut berperan. Pertanyaan ini memberi tahu kita apakah hasil nol yang mungkin kita lihat dapat dipercaya memberi tahu kita bahwa pengobatan tidak berhasil. Sebagian besar metode sia-sia menjawab pertanyaan pertama. Misalnya, daya kondisional adalah probabilitas kondisional bahwa hasil di akhir uji coba akan signifikan secara statistik, mengingat hasil saat ini dan proyeksi data masa depan. Daya kondisional yang rendah berarti kemungkinan besar akan terjadi hasil nol. Kami berpendapat bahwa kalkulasi daya tanpa syarat yang direvisi , yaitu mengulang kalkulasi daya asli tetapi menggunakan estimasi parameter gangguan yang direvisi, adalah alat yang berguna untuk menjawab pertanyaan kedua. Alat-alat yang digunakan harus ditentukan terlebih dahulu dalam protokol. Perencanaan awal sangat penting untuk menjaga integritas dan reproduktifitas penelitian.
2 Tinjauan Informasi, Skor Z, dan Nilai B
2.1 Pengaturan Khusus






| Jumlah tampilan | ||||||
|---|---|---|---|---|---|---|
| Kekuatan tanpa syarat | 1 | 2 | 3 | 4 | 5 | 6 |
| 0,80 | 0.200 | 0,259 | 0.312 | 0.356 | 0.392 | 0.422 |
| 0,85 | 0,150 | 0.204 | 0.256 | 0.300 | 0,337 tahun | 0,368 tahun |
| 0,90 | 0.100 | 0,147 tahun | 0.196 | 0.238 | 0,275 | 0.306 |




| Jumlah tampilan | ||||||
|---|---|---|---|---|---|---|
| Kekuatan tanpa syarat | 1 | 2 | 3 | 4 | 5 | 6 |
| 0,80 | 0.200 | 0.203 | 0.206 | 0.209 | 0.212 | 0.214 |
| 0,85 | 0,150 | 0.153 | 0.156 | 0.159 | 0.161 | 0.163 |
| 0,90 | 0.100 | 0.102 | 0,105 | 0.107 | 0.110 | 0.112 |



3.4.2 Plot Interval yang Diprediksi
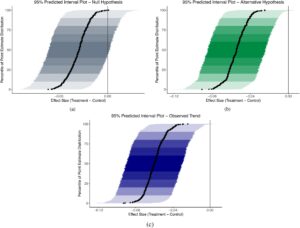
Li et al. [ 14 ] mengusulkan plot interval terprediksi (PIPS), sebuah alat visualisasi yang merangkum hasil dari simulasi interval terprediksi yang berulang, dan merekomendasikan konstruksi PIPS dengan asumsi yang berbeda untuk mekanisme pembangkitan data dari data yang tidak teramati. Prosedurnya adalah sebagai berikut:
-
- Buatlah asumsi tentang mekanisme pembangkitan data. Contohnya meliputi tren yang diamati, hipotesis nol, dan hipotesis alternatif.
- Dapatkan estimasi titik prediksi M (angka besar; dalam contoh, kami menggunakan 500) dan interval prediksi terkait untuk probabilitas cakupan tertentu (kami menggunakan 95%).
- Gambarkan estimasi titik yang diprediksi menggunakan titik-titik padat dan interval prediksi yang sesuai sebagai garis-garis padat yang melalui titik-titik tersebut.
- Li et al. [ 14 ] mengusulkan pengelompokan estimasi dan penggunaan kecerahan garis horizontal untuk menunjukkan nilai yang paling dekat dengan statistik yang diinginkan, seperti nilai rata-rata atau median pada beberapa simulasi. Dalam contoh kami, kami menggunakan median.
- Li et al. [ 14 ] mengusulkan agar pengelompokan dilakukan dengan menggunakan nilai fungsi kepadatan probabilitas bersyarat (CPDF) yang diestimasikan yang diperoleh dengan estimasi kepadatan kernel, dengan data interim yang diamati. Modus dapat diekstraksi dengan memperoleh estimasi titik dengan nilai estimasi CPDF tertinggi, dan menggunakan warna yang lebih cerah untuk estimasi yang paling dekat dengan modus.
- Alternatifnya, kita dapat menggunakan persentil dari distribusi estimasi titik dan menggunakan warna yang lebih terang untuk estimasi yang paling dekat dengan median. Pendekatan ini diilustrasikan dalam contoh kita.
- Tunjukkan nilai nol dari parameter yang diinginkan menggunakan garis vertikal pada plot.


| Selang | Memperkirakan | Lebih rendah | Atas | Lebar interval |
|---|---|---|---|---|
| Interval keyakinan yang diamati | -0,059 | -0,102 | -0,017 | 0,085 |
| PI di bawah nol | -0,026 | -0,057 | 0,005 | 0,062 |
| PI di bawah alternatif | -0,050 | -0,081 | -0,020 | 0,061 tahun |
| PI di bawah tren yang diamati | -0,056 | -0,086 | -0,026 | 0,060 |



| Jumlah tampilan | |||||
|---|---|---|---|---|---|
| l1 | l2 | l3 | l4 | Melayang | |
| γ=−4 | -1,0607 | -0,0037 | 0,9761 tahun | 2.0141 | 3.0572 |
| γ=−2 | -0,6029 | 0.3572 | tahun 1927 | 2.0141 | 3.1222 |
| γ=+2 | 0.2788 | 1.0364 | 1.5654 | 2.0141 | 3.5353 |



5 Diskusi
Pemantauan kegagalan harus dipertimbangkan dalam fase desain uji coba dan harus mempertimbangkan faktor-faktor seperti fase uji coba, tingkat keseriusan penyakit, kebutuhan untuk menemukan pengobatan yang efektif secepat mungkin, dan dampak keputusan kegagalan pada kemampuan untuk menilai titik akhir sekunder dan keamanan. Misalnya, dalam uji coba tahap awal, kesalahan tipe II sangat serius karena dapat menyebabkan penghentian pengujian lebih lanjut terhadap pengobatan yang efektif. Uji coba multi-lengan dalam penyakit mematikan seperti penyakit virus Ebola mungkin memiliki pedoman kegagalan yang lebih agresif untuk menghentikan lengan yang berkinerja buruk dan hanya melanjutkan pengobatan yang menjanjikan.
Pemantauan kesia-siaan dapat menghentikan uji coba yang gagal dan memungkinkan sumber daya dialokasikan kembali ke agen yang lebih menjanjikan. Daya bersyarat dan daya tanpa syarat yang direvisi berguna untuk menjawab dua pertanyaan terpisah: (1) Apakah hasil akhir akan nol? dan (2) Apakah hasil nol akan bermakna? Jika jawabannya masing-masing adalah ya dan tidak, kelanjutan tidak ada gunanya. Pembatasan stokastik adalah pedoman seperti “pertimbangkan untuk berhenti jika daya bersyarat turun di bawah 0,20.” Properti bergantung pada efek perlakuan apa yang diasumsikan. Efek perlakuan yang diamati yang umum digunakan cukup bervariasi dan dapat menyebabkan hilangnya daya yang substansial. Efek perlakuan yang dihipotesiskan awalnya stabil dan menyebabkan hilangnya daya minimal, tetapi mungkin tidak realistis mengingat data yang diamati. Daya prediktif adalah alternatif Bayesian yang merata-ratakan daya bersyarat atas distribusi posterior efek perlakuan, mengingat datanya. Daya prediktif dapat dilihat sebagai kompromi antara penggunaan efek perlakuan yang dihipotesiskan awalnya vs. efek perlakuan yang diamati.
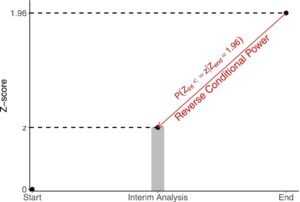
Kekuatan kondisional terbalik menghindari masalah efek pengobatan. Alih-alih mengondisikan hasil sementara dan memproyeksikan ke akhir penelitian, kami mengondisikan (hampir) mencapai signifikansi statistik di akhir uji coba dan bertanya “Berapa probabilitas kita akan melihat hasil yang setidaknya tidak menjanjikan seperti yang kita lihat pada analisis sementara?” Probabilitas ini tidak bergantung pada efek pengobatan. Jika hasil yang suram seperti itu sangat tidak mungkin terjadi di antara uji coba yang akhirnya mencapai signifikansi statistik, kami dapat yakin bahwa uji coba kami tidak akan termasuk di antara mereka.
Plot interval terprediksi merupakan pelengkap yang berguna untuk daya kondisional yang menawarkan estimasi, bukan pengujian, perspektif. Kami berulang kali mensimulasikan dan menambahkan data masa depan ke hasil saat ini dan menghitung interval keyakinan masa depan untuk efek perlakuan. Ini memberikan gambaran grafis daya kondisional dan membedakan antara daya kondisional rendah yang disebabkan oleh hasil sementara yang sangat buruk atau oleh variabilitas yang jauh lebih tinggi dari yang diharapkan, yang mengarah ke interval keyakinan yang sangat lebar.
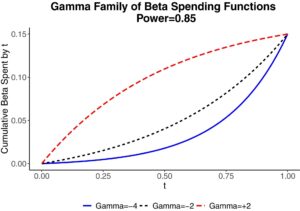
Fungsi pengeluaran beta serupa dengan fungsi pengeluaran alfa, tetapi tingkat kesalahan pengeluarannya adalah tipe II, bukan tipe I. Seperti halnya pengeluaran alfa, kita dapat membelanjakan secara konservatif atau agresif melalui berbagai pilihan fungsi pengeluaran.
Semua metode di atas bermanfaat dan harus diperlakukan sebagai pedoman, bukan aturan yang ketat. Pemantauan kesia-siaan dapat sedikit menurunkan rasio kesalahan tipe I karena kelanjutan mungkin telah menghasilkan manfaat yang signifikan secara statistik. Beberapa orang telah menganjurkan pemulihan rasio kesalahan tipe I yang hilang dengan memodifikasi batasan efikasi untuk memperhitungkan pemantauan kesia-siaan. Praktik ini harus dihindari karena rasio kesalahan tipe I akan dikendalikan hanya jika pedoman kesia-siaan diikuti dengan ketat. Bahkan batasan efikasi adalah pedoman, bukan aturan, dalam arti bahwa faktor-faktor lain hampir selalu berperan saat membuat keputusan penghentian. Pedoman kesia-siaan biasanya dianggap kurang mengikat. Keputusan akhir hampir selalu bergantung pada banyak faktor lain, seperti apakah (1) uji coba akan tetap memberikan informasi yang berguna tentang keamanan atau titik akhir sekunder, (2) pendaftaran telah selesai dan biaya kelanjutan rendah, (3) penyakitnya ringan dan intervensi digunakan secara luas, sehingga kelanjutan mungkin diperlukan untuk menunjukkan bahwa itu tidak berhasil. Meninggalkan uji coba yang mengecewakan memiliki konsekuensi. Pertimbangkan hasil alat statistik di atas dengan pertimbangan ekstra-statistik sebelum membuat keputusan akhir.