ABSTRAK
Sementara data mengenai volatilitas tersirat tersedia untuk sejumlah besar aset, hal ini lebih jarang terjadi pada kovolatilitas tersirat. Kami memperkenalkan pendekatan baru berdasarkan model Wishart statis dan dinamis untuk memecahkan masalah data yang hilang ini. Pertama-tama kami membahas identifikasi parameter model Wishart (ruang keadaan nonlinier) dari volatilitas tersirat yang diamati. Ditunjukkan bahwa parameter model Wishart teridentifikasi, mungkin hingga beberapa tanda. Kemudian kami memperoleh pendekatan penyaringan untuk kovolatilitas tersirat dan menerapkannya pada berbagai aplikasi keuangan. Masalah identifikasi dalam model dinamis lain berdasarkan dekomposisi spektral, logaritma matriks, dan dekomposisi volatilitas-korelasi juga dibahas. Kami juga membahas implikasi hasil ini untuk pemodelan matriks kovariansi yang terealisasi, ketika yang terakhir ini sepenuhnya dapat diamati, dengan mengusulkan uji spesifikasi baru untuk model tipe Wishart.
1 Pendahuluan
Makalah ini membahas masalah observabilitas parsial saat menganalisis dinamika gabungan (historis) harga derivatif seperti harga opsi Eropa. Untuk memperbaiki ide-ide tersebut, mari kita pertimbangkan opsi beli at-the-money dengan waktu jatuh tempo 1 tahun. Opsi-opsi ini dapat ditulis pada satu aset, atau pada indeks yang dihitung secara linier, atau nonlinier dari beberapa aset dasar. Dalam kasus terakhir, kita dapat membedakan dua jenis indeks berikut:


| ATM | Bursa Efek | ATM Geometris | |
|---|---|---|---|
| Jenis | opsi saham | pilihan | pilihan keranjang |
| Hasil | (SSayaBahasa Indonesia:T+1/SSayaBahasa Indonesia:T-1)+ | (SSayaBahasa Indonesia:T+1-SJBahasa Indonesia:T+1)+ | ∏Saya=1N(SSayaBahasa Indonesia:T+1/SSayaBahasa Indonesia:T)ASaya-1+ |
| volatilitas (kuadrat) | kamuaku aku akuBahasa Indonesia:T | kamuaku aku akuBahasa Indonesia:T+kamuJJBahasa Indonesia:T-2kamuaku jBahasa Indonesia:T | A’kamuTA |






















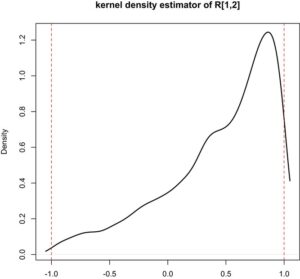
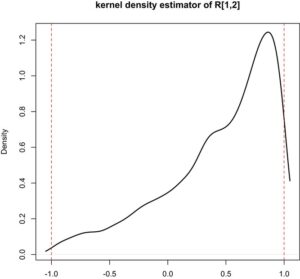


| 10% | 25% | 50% | 75% | 90% |
| 0,026 | 0,036 hari | 0,051 tahun | 0,069 tahun | 0,084 tahun |
| 10% | 25% | 50% | 75% | 90% |
| 0,024 | 0,032 | 0,043 tahun | 0,055 | 0,063 tahun |


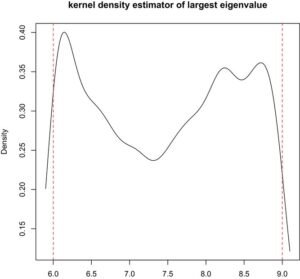
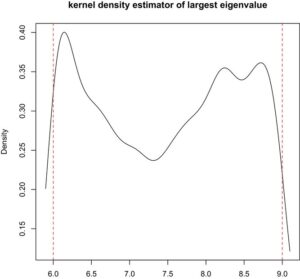





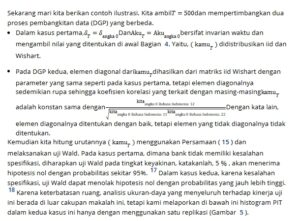
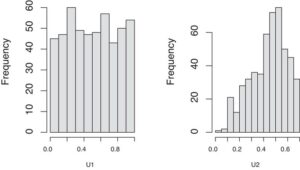








6. Penutup
Padahal data tentang volatilitas tersirat (BS) tersedia untuk sejumlah besar aset, hal ini jarang terjadi pada kovolatilitas tersirat yang, meskipun tersedia, kurang dapat diandalkan karena kurangnya aktivitas di pasar derivatif terkait. Kami telah memperkenalkan pendekatan berdasarkan model Wishart statis dan dinamis untuk memecahkan masalah observabilitas parsial. Identifikasi parametrik didasarkan pada pembatasan positif nonlinier antara kovolatilitas dan volatilitas, karena kepastian positif dari matriks volatilitas. Hal ini memungkinkan pengembangan pendekatan penyaringan kovolatilitas tersirat, dengan mempertimbangkan estimasi dan risiko penyaringan. Kami telah melihat bagaimana pendekatan “penyaringan” berbasis model ini dapat digunakan untuk memprediksi harga derivatif keranjang atau untuk memperkirakan risiko tersirat maksimal atau kinerja Sharpe.
Sementara pendekatan ini terutama dianjurkan untuk kasus di mana suku-suku off-diagonal dari matriks volatilitas tidak diamati, untuk menentukan harga derivatif yang belum ada atau tidak cukup likuid, pendekatan ini juga dapat digunakan dalam kasus-kasus di mana matriks volatilitas diamati sepenuhnya. Misalnya, ini dapat terjadi ketika seseorang tidak berfokus pada matriks volatilitas tersirat, tetapi pada matriks kovariansi yang terealisasi, yang suku-suku off-diagonalnya dapat diamati dengan lebih mudah. Secara khusus, terdapat banyak literatur tentang pemodelan rangkaian matriks kovariansi yang terealisasi tersebut menggunakan model tipe Wishart. Dalam kasus-kasus ini dengan pengamatan penuh terhadap matriks, kami juga telah menunjukkan di Bagian 4.4 bahwa pendekatan yang dikembangkan dalam makalah ini dapat berfungsi sebagai alat untuk uji spesifikasi model.
Dalam makalah kami, kami terutama berfokus pada model Wishart 21 , karena ini adalah salah satu distribusi parametrik paling populer untuk matriks simetris positif definit acak. Meskipun demikian, hasilnya juga dapat diadaptasi ke banyak distribusi matriks parametrik lainnya dengan jumlah parameter yang sama. Misalnya, distribusi Wishart invers adalah distribusi
kamu
–
1
, Di mana
kamu
mengikuti distribusi Wishart pusat. Mudah untuk memeriksa bahwa, untuk distribusi ini, parameter skala matriks positif pasti simetris
Aku
juga mengendalikan ekspektasi dari istilah diagonal dan korelasinya. Sebagai konsekuensinya, seseorang dapat mengharapkan bahwa hasil identifikasi serupa terus berlaku dalam model Wishart terbalik tersebut. Demikian pula, hal yang sama dapat dikatakan tentang matriks-
F
distribusi. Tak perlu dikatakan lagi, asumsi distribusi parametrik yang berbeda mengarah pada distribusi tersirat yang berbeda untuk kovolatilitas. Jadi ketika kovolatilitas pada dasarnya tidak teramati, tidak mungkin untuk mengetahui asumsi parametrik mana yang terbaik. Dengan kata lain, hasil identifikasi peka terhadap asumsi identifikasi parametrik. “Batas” ini diharapkan, dan umum untuk semua pendekatan imputasi ekonometrik berdasarkan asumsi parametrik. Seperti contoh dekomposisi korelasi-volatilitas di Bagian 5 menunjukkan, identifikasi berdasarkan asumsi parametrik adalah skenario terbaik yang dapat kita capai ketika kovolatilitas tidak dapat diamati, karena tidak mungkin untuk mengidentifikasi matriks korelasi, tanpa asumsi parametrik pada yang terakhir ini.