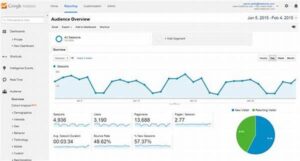
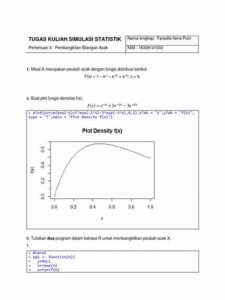
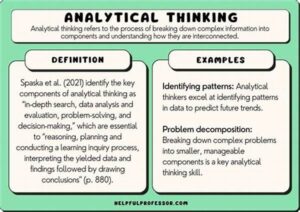
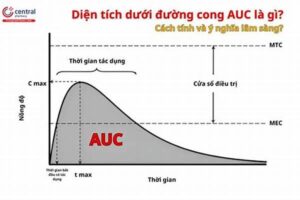
Abstrak
Kami mempelajari konvergensi aliran gradien untuk pelatihan jaringan saraf dalam. Sementara jaringan saraf residual (ResNet) adalah contoh populer dari arsitektur yang sangat dalam, pelatihannya merupakan masalah pengoptimalan yang menantang, terutama karena non-konveksitas dan non-koersivitas objektif. Namun, dalam aplikasi, tugas-tugas tersebut berhasil diselesaikan dengan algoritme pengoptimalan sederhana seperti penurunan gradien. Untuk lebih memahami fenomena ini, kami fokus di sini pada model “medan-rata-rata” dari ResNet yang sangat dalam dan lebarnya sewenang-wenang, yang diparameterisasi oleh ukuran probabilitas pada set produk lapisan dan parameter, dan dengan marginal konstan pada set lapisan. Memang, dalam kasus jaringan saraf dangkal, model medan rata-rata telah terbukti mendapat manfaat dari lanskap kerugian yang disederhanakan dan jaminan teoritis yang baik ketika dilatih dengan aliran gradien sehubungan dengan metrik Wasserstein pada set ukuran probabilitas. Termotivasi oleh pendekatan ini, kami mengusulkan untuk melatih model kami dengan aliran gradien sehubungan dengan jarak transportasi optimal bersyarat (COT): pembatasan jarak Wasserstein klasik yang menegakkan kondisi marginal kami. Dengan mengandalkan teori aliran gradien dalam ruang metrik, pertama-tama kami menunjukkan ketepatan persamaan aliran gradien dan konsistensinya dengan pelatihan ResNets pada lebar terbatas. Dengan melakukan analisis Polyak–Łojasiewicz lokal, kami kemudian menunjukkan konvergensi aliran gradien untuk inisialisasi yang dipilih dengan baik: jika jumlah fitur terbatas tetapi cukup besar dan risikonya cukup kecil pada inisialisasi, aliran gradien konvergen ke peminimal global. Ini adalah hasil pertama dari jenis ini untuk ResNets yang sangat dalam dan lebarnya sewenang-wenang. Selain itu, pekerjaan ini merupakan kesempatan untuk mempelajari metrik COT secara lebih rinci, khususnya formulasi dinamisnya. Beberapa hasil kami dalam arah ini mungkin menarik dengan sendirinya.