Abstrak
Keberlanjutan telah menjadi salah satu tujuan utama dalam semua aktivitas manusia dan, khususnya, dalam lingkungan manufaktur. Dalam makalah ini, kami mempertimbangkan masalah penjadwalan job shop yang fleksibel dengan tujuan meminimalkan konsumsi energi. Seperti diketahui bahwa sebagian besar konsumsi energi terjadi saat mesin menyala dan diam, masalah yang dibahas mencakup kemungkinan mematikan dan menghidupkan mesin di antara operasi pemrosesan. Untuk mendekatkan masalah dengan berbagai macam masalah dunia nyata yang dicakupnya, kami menyertakan dua faktor relevan: rute nonlinier dan efek pembelajaran berbasis posisi. Masalah yang ditangani dijelaskan secara formal melalui model pemrograman linier bilangan bulat campuran. Kami mengusulkan heuristik konstruktif, dua jenis lingkungan tempat kami membangun skema pencarian lokal dan tiga metaheuristik, yaitu, pencarian lingkungan variabel umum, prosedur pencarian adaptif acak serakah, dan simulasi anil. Kami melakukan sejumlah besar eksperimen untuk mengevaluasi kinerja metode yang diperkenalkan pada instans berukuran kecil dan berukuran besar. Dalam kasus berukuran besar, pencarian lingkungan variabel umum yang menggabungkan dua lingkungan menjadi satu metode sangat efektif. Dalam kasus berukuran kecil dengan solusi optimal yang diketahui, prosedur pencarian adaptif acak yang rakus menemukan solusi yang, secara rata-rata, berada dalam 0,22% dari solusi optimal.
1 Pendahuluan
Flexible job shop (FJS) adalah masalah penjadwalan yang menjadi inti lingkungan manufaktur yang terkenal karena banyaknya aplikasi praktis. Masalah ini bersifat NP-keras karena mencakup masalah penjadwalan job shop (JS), yang dikenal sebagai NP-keras (Garey et al., 1976 ), sebagai kasus khusus. Karena relevansinya dan kesulitan penyelesaiannya, berbagai macam metode heuristik dan metaheuristik telah dikembangkan dalam literatur terkini untuk penyelesaiannya, lihat Dauzère-Pérès et al. ( 2024 ) dan Xie et al. ( 2019 ). Pada saat yang sama, karena banyaknya masalah dunia nyata yang termasuk dalam cakupannya, berbagai aspek praktis telah disertakan dalam formulasinya. Dalam karya ini, kami mempertimbangkan masalah penjadwalan FJS dengan rute nonlinier dan efek pembelajaran berbasis posisi. Dengan efek pembelajaran, kami maksudkan bahwa waktu pemrosesan operasi dalam mesin bergantung pada posisi yang ditempati operasi dalam mesin, yaitu, kami mempertimbangkan efek pembelajaran berbasis posisi. Kami merujuk pada Gupta dan Gupta ( 1988 ), Biskup ( 1999 ), dan Cheng dan Wang ( 2000 ) sebagai aplikasi pertama dari ide efek pembelajaran dalam masalah penjadwalan. Dengan rute nonlinier, kami merujuk pada fakta bahwa operasi yang merupakan pekerjaan tidak harus mengikuti urutan linier untuk eksekusinya, tetapi hubungan prioritasnya diberikan oleh grafik asiklik yang diarahkan secara sembarangan. Secara khusus, ini memungkinkan operasi yang berbeda dari pekerjaan yang sama untuk diproses secara paralel. (Lihat Birgin et al., 2014 , untuk detailnya.) Perlu dicatat bahwa penyertaan rute nonlinier dalam FJS memungkinkan untuk mengatasi masalah penjadwalan toko percetakan online (OPS), masalah nyata dan menantang dalam industri percetakan saat ini (Araujo et al., 2024a, 2024b (Birgin et al., 2015 ; Lunardi et al., 2020 , 2021 ; Araujo et al., 2024a , 2024b ). Seperti yang dijelaskan dalam Lunardi et al. ( 2020 ), dalam masalah penjadwalan OPS, pesanan produk yang akan diproduksi, seperti buku, brosur, pamflet, album foto, dan banyak lainnya, diterima secara online. Setiap jenis produk memiliki rencana produksi yang berbeda, tetapi semuanya melibatkan operasi pencetakan. Ketika sejumlah besar pesanan tercapai, untuk menghemat bahan baku (kertas), masalah stok pemotongan diselesaikan dengan menggabungkan operasi pencetakan dari berbagai pesanan yang ditempatkan. Pesanan yang operasi pencetakannya digabungkan membentuk satu pekerjaan. Dengan demikian, pekerjaan dalam masalah penjadwalan OPS, yang terdiri dari serangkaian operasi heterogen dengan batasan prioritas yang sewenang-wenang, sangat beragam. Dalam studi masalah OPS yang dilakukan oleh Lunardi et al. ( 2020 ,2021 ), beberapa fitur yang mempersulit seperti periode tidak tersedianya mesin, operasi yang dapat dilanjutkan, waktu penyiapan yang bergantung pada urutan, tumpang tindih sebagian operasi dengan batasan prioritas, waktu rilis, dan operasi tetap telah ditangani. Namun, faktor yang mempersulit masalah dunia nyata ini diabaikan: beberapa operasi dilakukan oleh operator manusia. Tugas-tugas ini meliputi tata letak bahan yang akan dicetak dengan bantuan komputer, merakit berbagai bagian buku dan menyusun sampul, menangani alat pemotong, mengemas produk jadi, dan lain-lain. Tugas-tugas yang dilakukan oleh operator manusia ini tunduk pada efek pembelajaran. Dengan asumsi bahwa operator manusia belajar dengan berulang kali melakukan operasi yang sama, masuk akal untuk mengatakan bahwa, dalam batasan tertentu,Eksekusi akan lebih cepat dariMeskipun ada alternatif lain, hal ini memunculkan gagasan tentang model efek pembelajaran berdasarkan posisi operasi dalam daftar operasi yang akan dilakukan oleh operator yang sama.
Dalam karya ini, kami menyadari bahwa keberlanjutan telah memperoleh kepentingan utama selama beberapa dekade terakhir, menjadi tujuan global utama. Secara sederhana, keberlanjutan berarti memenuhi kebutuhan saat ini tanpa memengaruhi generasi mendatang. Oleh karena itu, literatur terkini menyebut penjadwalan hijau sebagai masalah penjadwalan yang memperhitungkan keselamatan pekerja (Gong et al., 2019 ), kesejahteraan pekerja (Destouet et al., 2024 ), pelestarian mesin (Wu dan Sun, 2018 ), emisi karbon (Zhu et al., 2020 ; Li dan Chen, 2023 ), emisi kebisingan dan konsumsi energi, dan/atau biaya (Gahm et al., 2016 ), antara lain. Energi, khususnya, telah menjadi titik fokus dalam Agenda 2030 untuk Pembangunan Berkelanjutan (Majelis, 2015 ) yang diadopsi pada KTT Pembangunan Berkelanjutan Perserikatan Bangsa-Bangsa pada tahun 2015. Karena alasan ini, dalam karya ini, kami mempertimbangkan tujuan sadar energi untuk meminimalkan konsumsi energi. Seperti diketahui bahwa sebagian besar konsumsi energi terjadi saat mesin menyala dan diam, masalah yang dipertimbangkan mencakup kemungkinan mematikan dan menghidupkan mesin di antara operasi pemrosesan. Karena sebagian besar waktu energi yang dikonsumsi berasal dari sumber yang tidak terbarukan, ada hubungan langsung antara konsumsi energi dan emisi karbon, yang mengintensifkan efek pemanasan.
Skema konsumsi energi yang berlaku memperhitungkan biaya menghidupkan dan mematikan mesin, biaya setiap mesin dalam memproses setiap operasi, biaya untuk menjaga mesin tetap menyala dan diam, dan biaya yang terkait dengan menjaga fasilitas tetap berjalan. Perlu dicatat bahwa kemungkinan mematikan dan menghidupkan mesin di antara pemrosesan dua operasi berturut-turut dipertimbangkan jika ini menghasilkan biaya yang lebih rendah daripada biaya untuk menjaga mesin tetap menyala dan diam. Namun, pada saat yang sama mungkin lebih murah, mematikan dan menghidupkan mesin mungkin memakan waktu lebih lama, meningkatkan waktu penyelesaian satu atau lebih pekerjaan. Dengan demikian, fungsi tujuan dari masalah ini tidak teratur. Titik awal dari pekerjaan ini adalah pemodelan masalah yang sedang dipertimbangkan dengan pemrograman linier bilangan bulat campuran (MILP). Pemodelan ada dua. Di satu sisi, ini bertujuan untuk menggambarkan masalah secara tepat. Di sisi lain, ini digunakan untuk memecahkan contoh-contoh kecil dari masalah dengan penyelesai yang tepat untuk memeriksa efektivitas metode yang diusulkan. Dalam sekuelnya, kami mengembangkan heuristik penjadwalan daftar konstruktif dan dua lingkungan yang berbeda: satu berdasarkan penghapusan dan penyisipan kembali satu operasi dan yang lainnya berdasarkan penghapusan satu operasi, penghancuran, penyisipan kembali, dan rekonstruksi. Atas dasar lingkungan tersebut, dua algoritma pencarian lokal dan tiga metaheuristik dikembangkan. Metaheuristik yang dipertimbangkan adalah simulasi annealing (SA), prosedur pencarian adaptif acak serakah (GRASP), dan pencarian lingkungan variabel umum (GVNS).
Sisa dari karya ini disusun sebagai berikut. Tinjauan pustaka disajikan di Bagian 2. Di Bagian 3 , kami secara formal menggambarkan masalah dan merumuskannya sebagai masalah MILP. Di Bagian 4 dan 5 , kami memperkenalkan heuristik konstruktif dan dua strategi pencarian lokal, masing-masing. Di Bagian 6 , kami menggambarkan metaheuristik yang dipertimbangkan. Eksperimen numerik yang luas disajikan di Bagian 7. Bagian 8 mencakup kesimpulan dan arahan untuk pekerjaan di masa mendatang.
Notasi . Simbolmewakili konstanta matematika yang nilainya sekitar 2,71828,adalah logaritma natural,, Dan.
2 Tinjauan Pustaka
Berikut ini, kami menyajikan tinjauan pustaka dari makalah yang membahas konsumsi energi di lingkungan FJS. Perlu dicatat bahwa, sementara beberapa dari mereka memperhitungkan efek pembelajaran, tidak ada dari mereka yang mempertimbangkan rute nonlinier. Desain model untuk masalah FJS dengan minimalisasi konsumsi energi telah menjadi subjek dari beberapa publikasi baru-baru ini. Dalam Mouzon et al. ( 2007 ), disoroti bahwa, dalam masalah penjadwalan, bagian penting dari konsumsi energi sesuai dengan mesin nonbottleneck yang tetap menyala dan diam. Berdasarkan premis ini, Zhang et al. ( 2017a , 2017b , 2017c ); Meng et al. ( 2019 ) mengusulkan model matematika untuk masalah penjadwalan FJS, dengan tujuan meminimalkan konsumsi energi dan memungkinkan mesin untuk dihidupkan dan dimatikan di antara operasi pemrosesan. (Model pemrograman kendala dan modifikasi kecil pada model MILP yang diusulkan dalam Meng et al., 2019 , disajikan dalam Ham et al., 2021. ) Dalam Meng et al. ( 2019 ) perbandingan dengan model yang sebelumnya diusulkan dalam Zhang et al. ( 2017a , 2017b , 2017c ) disajikan, menunjukkan bahwa model yang diusulkan dalam Meng et al. ( 2019 ) lebih efektif/efisien ketika mencoba memecahkan contoh kecil dengan metode yang tepat. Model yang diperkenalkan dalam karya saat ini, yang menggunakan variabel biner yang sama dengan model 2.2 yang diusulkan oleh Meng et al. ( 2019 ), didasarkan pada model yang diusulkan oleh Araujo et al. ( 2024b ). Pilihan untuk variabel biner menunjukkan apakah operasidikaitkan dengan posisidari sebuah mesindidorong oleh kebutuhan untuk memodelkan efek pembelajaran yang bergantung pada posisi yang diambil oleh suatu operasi di dalam mesin (semakin tinggi posisi, semakin pendek waktu pemrosesan). Jika dibandingkan dengan model dalam Meng et al. ( 2019 ), model ini juga mencakup hubungan prioritas antara operasi dari pekerjaan yang sama yang diberikan oleh grafik asiklik berarah sembarang (rute nonlinier) dan efek pembelajaran pada waktu pemrosesan. Jika dibandingkan dengan model yang disajikan oleh Araujo et al. ( 2024b ), model ini berbeda dalam fungsi objektif, yang menyiratkan dalam mempertimbangkan, misalnya, kemungkinan menghidupkan dan mematikan mesin di antara operasi pemrosesan. Selain itu, perlu disebutkan bahwa keberadaan model dalam karya ini berfungsi untuk menggambarkan dengan jelas masalah yang sedang dipertimbangkan.
Dalam Li et al. ( 2020 ), lingkungan FJS dengan sumber daya ganda dan minimisasi konsumsi energi dipertimbangkan. Masalah ini dijelaskan melalui model MILP. Untuk solusinya, berbagai lingkungan sekitar, pencarian lokal, mekanisme memulai ulang, dan metode optimasi berdasarkan burung yang bermigrasi diusulkan. Dalam Lu et al. ( 2019 ), masalah meminimalkan konsumsi energi yang dikombinasikan dengan waktu penyelesaian dalam lingkungan FJS dipertimbangkan. Karena makespan dikalikan dengan konsumsi energi per satuan waktu, komponen fungsi tujuan ini sesuai untuk mempertimbangkan konsumsi energi relatif terhadap menjaga pabrik tetap berjalan. Ini berarti bahwa tujuan dapat dilihat sebagai meminimalkan konsumsi energi saja. Untuk masalah ini, algoritma optimasi gelombang air dipertimbangkan.
Dalam Lei et al. ( 2016 ), konflik antara meminimalkan konsumsi energi dan menyeimbangkan antara jalur kerja dipelajari. Masalah dengan dua tujuan dimodelkan sebagai masalah bi-objektif dan algoritma lompat katak acak diusulkan. Ren et al. ( 2020 ) mempertimbangkan lingkungan FJS dengan jenis rute nonlinier tertentu: beberapa operasi adalah operasi standar yang harus diproses pada mesin sementara yang lain adalah operasi perakitan yang harus diproses di stasiun perakitan dan memerlukan serangkaian operasi yang harus diselesaikan sebelumnya. Tujuannya adalah meminimalkan makespan dan konsumsi energi. Untuk masalah bi-objektif ini, metaheuristik hibrid yang menggabungkan algoritma genetika dengan pengoptimalan segerombolan partikel diusulkan. Menurut Wu dan Sun ( 2018 ), mematikan dan menghidupkan mesin serta mengendalikan kecepatan mesin beroperasi dianggap sebagai cara untuk mengurangi konsumsi energi. Masalah yang dipertimbangkan secara bersamaan mengoptimalkan makespan, konsumsi energi, dan berapa kali mesin perlu dimatikan dan dihidupkan. Untuk masalah ini, algoritma genetika nondominated sorted (NSGA-II) yang mengintegrasikan heuristik penjadwalan hijau diusulkan. Gong et al. ( 2019 ) mempertimbangkan masalah multiobjektif dengan lima tujuan, di antaranya, total biaya energi. Dalam lingkungan dengan harga listrik yang dinamis, mungkin menarik untuk memproses operasi selama periode malam, yang akan meningkatkan biaya tenaga kerja. Oleh karena itu, biaya lain yang dipertimbangkan adalah biaya tenaga kerja. Tiga tujuan lainnya adalah beban maksimum mesin, jumlah beban semua mesin, dan makespan. Untuk masalah ini, metode NSGA-III dirancang. Dalam Wu et al. ( 2019 ), masalah yang sedang dipertimbangkan adalah masalah manufaktur produk kedirgantaraan dan militer, di mana, karena siklus pemrosesan komponen yang panjang, keausan pahat memengaruhi pemrosesan pekerjaan. Masalah ini sesuai dengan lingkungan FJS dan tujuannya adalah untuk meminimalkan makespan dan konsumsi energi secara bersamaan, dengan mempertimbangkan efek kerusakan waktu pemrosesan. Model kerusakan bergantung pada waktu dan model konsumsi energi mengikuti profil konsumsi energi yang sangat spesifik untuk operasi yang semuanya merupakan operasi pemotongan. Untuk masalah ini, algoritma optimasi hibrida bi-objektif yang terinspirasi dari merpati dan simulasi anil dikembangkan.
Dalam Li dan Chen ( 2023 ), masalah bi-objektif di mana makespan dan emisi karbon diminimalkan dipertimbangkan. Waktu pemrosesan dipengaruhi oleh efek pembelajaran Dejong (De Jong, 1957 ), tetapi emisi karbon dari pemrosesan setiap operasi dianggap tetap dan tidak bergantung pada waktu pemrosesannya. Oleh karena itu, bahkan jika ada hubungan langsung antara konsumsi energi dan emisi karbon, minimisasi yang satu tidak akan setara dengan minimisasi yang lain, karena konsumsi energi terkait dengan waktu pemrosesan. Untuk masalah ini, algoritma pencarian sparrow multiobjektif diusulkan. Untuk ikhtisar emisi karbon sebagai ukuran kinerja dalam industri manufaktur, lihat Laurent et al. Baru-baru ini, Gong et al. ( 2024 ) menangani minimisasi makespan dan konsumsi energi secara simultan dalam lingkungan FJS. Dalam skenario yang dipertimbangkan, beberapa operasi memiliki rute linier, sementara yang lain independen dan tidak memiliki hubungan preseden yang menghubungkannya dengan operasi lain mana pun. Perhitungan konsumsi energi tidak memperhitungkan kemungkinan mematikan dan menghidupkan mesin. Penulis mengusulkan algoritma yang didasarkan pada kombinasi Algoritma Memetic (MA) dan Algoritma Genetika Non-Dominated Sorting II (NSGA-II).
3 Definisi dan Perumusan Masalah
Masalah penjadwalan FJS merupakan perluasan dari masalah penjadwalan JS. Dalam JS, ada satu setoperasi dan satu setmesin. Untuk setiap operasi, sebuah mesindiberikan bahwa harus memproses operasiOperasi dibagi menjadi pekerjaanseperti yangDankapan pun. Operasi dari pekerjaan yang sama harus dijalankan dalam urutan linier yang telah ditentukan sebelumnya. “F” dalam FJS adalah singkatan dari “fleksibel” dan mengacu pada fakta bahwa alih-alih hanya ada satu mesinmampu memproses operasi, untuk setiap operasiada subset mesinyang dapat memprosesnya. Fitur ini dikenal sebagai fleksibilitas perutean. Tujuannya adalah untuk mengalokasikan setiap operasi ke suatu mesin dan memutuskan urutan mesin yang harus menjalankan operasi yang dialokasikan kepadanya sehingga prioritas antar operasi dihormati dan beberapa tujuan yang telah ditetapkan diminimalkan.
FJS dengan rute nonlinier merupakan perluasan dari masalah penjadwalan FJS. (Lihat Dauzère-Pérès et al., 2024 , §6.1, untuk pembahasan tentang berbagai sebutan yang diberikan dalam literatur untuk masalah ini.) Perluasan tersebut terdiri dari pelonggaran batasan prioritas operasi dari pekerjaan yang sama. Alih-alih urutan linier, hubungan dapat diberikan oleh grafik asiklik berarah (DAG) yang sembarangan. Pelonggaran ini sesuai dengan kasus praktis penting dalam industri percetakan modern. Misalnya, suatu pekerjaan mungkin untuk memproduksi sebuah buku dan operasinya dapat, secara sederhana, mencakup operasi tata letak yang mendahului semua yang lain, pencetakan (secara paralel dan tanpa prioritas di antara mereka) dari blok-blok lembar yang berbeda, dan, akhirnya, mengumpulkan semua blok lembar dan merekatkannya bersama-sama dengan sampul. Jelas, banyak masalah dunia nyata lainnya yang sesuai dengan deskripsi yang sama.
FJS dengan rute nonlinier dan efek pembelajaran berbasis posisi menambahkan unsur dunia nyata lebih lanjut ke dalam masalah. Dalam masalah penjadwalan klasik, diberikan operasidan sebuah mesin, waktu pemrosesanmesin itu perlu memproses operasi merupakan bagian dari data masalah. Namun, di dunia nyata, sebuah mesin (operator manusia) belajar melalui eksekusi operasi yang berulang. Pertama kali ia melakukan sesuatu, ia membutuhkan waktu, kedua kalinya ia melakukannya dengan lebih cepat, dan seterusnya. Itulah sebabnya kami menganggap dalam karya ini bahwa waktu pemrosesan aktual adalah fungsi yang bergantung pada waktu standar.dan pada posisi bahwa operasi menempati dalam daftar operasi yang akan dieksekusi oleh mesin Jika kita memanggil fungsi ini , maka kita katakan bahwa waktu pemrosesan operasi yang efektif , pada mesin , jika menempati posisi dalam daftar mesin , diberikan olehDalam karya ini, kami mempertimbangkan, Di manaadalah tingkat pembelajaran yang diberikan. Menambahkandan mengambil lantai memiliki tujuan untuk membulatkan nilai yang berpotensi bukan bilangan bulat.
Sekarang tinggal menyebutkan tujuan yang ingin diminimalkan. Secara umum, makespan dipertimbangkan. Dalam pekerjaan ini, kami mempertimbangkan konsumsi energi. Data yang kami miliki untuk tujuan ini, terkait dengan setiap mesin , adalah (a) seberapa banyak mesin mengkonsumsi, per satuan waktu, ketika memproses suatu operasi (disebut); (b) berapa banyak mesin yang dikonsumsi, per satuan waktu, ketika sedang menyala dan diam (disebut); (c) Berapa lama waktu yang dibutuhkan untuk menghidupkan mesin dan berapa konsumsi daya untuk menghidupkannya (disebutDan, masing-masing); (d) berapa lama waktu yang dibutuhkan untuk mematikan mesin dan berapa konsumsi daya untuk mematikannya (disebutDan, masing-masing); dan (e) berapa lama waktu maksimal mesin dapat menyala dan tidak aktif (disebut). Selain itu, kita juga mengetahui biaya energi, per satuan waktu, untuk menjalankan pabrik (disebut). Kami menganggap bahwa semua mesin menyala dan harus dimatikan pada akhirnya. Tentu saja, mesin harus dihidupkan sebelum memproses operasi pertamanya. Pabrik harus mulai berjalan saat mesin pertama dihidupkan dan berhenti berjalan saat mesin terakhir menyelesaikan proses penghentiannya. Dengan data ini, untuk setiap mesin dan setiap pasangan operasi yang diproses secara berurutan, kami harus memutuskan apakah mesin harus dimatikan dan dihidupkan lagi atau apakah harus tetap menyala dan diam. Tentu saja, jika keputusannya adalah untuk dimatikan dan dihidupkan, harus ada, antara penyelesaian satu operasi dan awal yang berikutnya, cukup waktu untuk mematikan dan menghidupkan mesin. Interval yang lebih besar dari minimum yang diberlakukan oleh hubungan prioritas antara dua operasi berturut-turut dapat memungkinkan mesin untuk dimatikan dan dihidupkan. Ini dapat menguntungkan dari sudut pandang konsumsi energi sambil meningkatkan waktu penyelesaian satu atau lebih pekerjaan. Oleh karena itu, fungsi tujuan yang dipertimbangkan dalam pekerjaan ini tidak teratur.
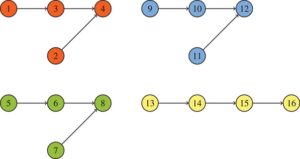
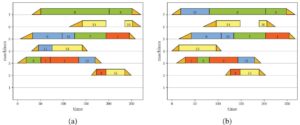
Dalam beberapa hal, mengingat adanya biaya, per unit waktu, untuk menjalankan pabrik, orang mungkin berpikir bahwa meminimalkan konsumsi energi hampir sama dengan meminimalkan makespan. Contoh berikut menunjukkan bahwa ini tidak terjadi. Mari kita pertimbangkan contoh dengan 16 operasi yang dibagi menjadi empat pekerjaan yang DAG prioritasnya ditunjukkan pada Gambar 1. Dalam contoh ini, kita memilikiDan. Ituset untukdan waktu pemrosesan standaruntukDanditunjukkan pada Tabel 1. Data dari (a) sampai (e) yang ditentukan pada paragraf sebelumnya dan menggambarkan konsumsi energi mesin ditunjukkan pada Tabel 2. Biaya per unit waktu untuk mengoperasikan pabrik adalah . Kami memecahkan kasus ini dengan mempertimbangkan dua tujuan yang berbeda. Dalam satu kasus, kami meminimalkan konsumsi energi. Dalam kasus lain, kami memecahkan masalah yang solusinya adalah solusi energi minimum di antara solusi yang meminimalkan makespan. Solusi untuk kedua masalah ini ditunjukkan pada Gambar 2a dan 2b , masing-masing. Solusi optimal dari masalah yang sesuai dengan meminimalkan konsumsi energi memiliki konsumsi energidan makespanSolusi untuk masalah kedua adalah konsumsi energidan makespan, yaitu, konsumsi yang lebih tinggi dan makespan yang lebih rendah. Ini jelas menunjukkan bahwa masalahnya berbeda.
| O | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
| 1 | — | 52 | 155 | — | — | — | — | — | 59 | — | — | 41 | — | — | 189 | — |
| 2 | 185 | 90 | 21 | 142 | — | — | 99 | — | — | — | — | — | — | 179 | 50 | — |
| 3 | 26 | 86 | — | — | 32 | — | — | 199 | — | — | 159 | 55 | — | — | — | — |
| 4 | — | — | 144 | 195 | — | — | — | — | 129 | — | 30 | 195 | 81 | 132 | 95 | 163 |
| 5 | — | 121 | 65 | 77 | 185 | — | 96 | 199 | 65 | 33 | — | — | — | — | 91 | — |
| 6 | 126 | — | — | 146 | — | — | — | — | 84 | 146 | 151 | 188 | — | 52 | — | 21 |
| 7 | 144 | 55 | 101 | 125 | 76 | 150 | 197 | 62 | — | — | 62 | 177 | — | 103 | — | — |
| k | γkproc | γkidle | τkon | γkon | τkoff | γkoff | τkidle |
|---|---|---|---|---|---|---|---|
| 1 | 87 | 8 | 15 | 750 | 11 | 550 | 162 |
| 2 | 86 | 5 | 11 | 638 | 14 | 812 | 290 |
| 3 | 81 | 8 | 19 | tahun 1653 | 14 | tahun 1218 | 358 |
| 4 | 85 | 8 | 15 | 930 | 11 | 682 | tahun 201 |
| 5 | 93 | 9 | 27 | Tahun 2025 | 13 | 975 | 333 |
| 6 | 92 | 9 | 28 | tahun 1960 | 18 | tahun 1260 | 357 |
| 7 | 96 | 5 | 19 | tahun 1672 | 19 | tahun 1672 | 668 |
Model yang diusulkan menggunakan variabel keputusan yang menentukan posisi setiap operasi dalam daftar setiap mesin. Ini adalah cara paling alami untuk memodelkan masalah karena memungkinkan untuk menghitung waktu pemrosesan efektif suatu operasi pada mesin, yang bergantung pada posisi operasi dalam daftar mesin. Model ini didasarkan pada model yang disajikan oleh Birgin et al. ( 2014 ) dan Araujo et al. ( 2024b ), tetapi seluruh bagian yang terkait dengan konsumsi energi dan keputusan apakah mesin harus tetap menyala dan diam atau harus dimatikan dan dihidupkan di antara pemrosesan dua operasi berturut-turut adalah baru. Variabel keputusan berbasis posisi untuk masalah penjadwalan awalnya digunakan oleh Wagner ( 1959 ) dan juga dipertimbangkan oleh Wilson ( 1989 ) dalam masalah penjadwalan flowshop.
Model MILP yang diusulkan adalah sebagai berikut:
Fungsi tujuan ( 1 ) menggambarkan minimisasi konsumsi energi. Fungsi tujuan tersusun dari penjumlahan dua suku kata. Suku pertama adalah penjumlahan semua mesin, sedangkan suku kedua merujuk pada konsumsi energi yang terkait dengan menjaga pabrik tetap beroperasi. Biaya yang terakhir hanyalah hasil kali konsumsi energi per satuan waktu dikalikan dengan waktu yang berlalu sejak mesin pertama dihidupkan hingga mesin terakhir dimatikan. Suku mesin menjumlahkan, untuk setiap mesin, konsumsi energi yang terkait dengan menghidupkan dan mematikannya, konsumsi energi yang terkait dengan operasi pemrosesan, dan konsumsi energi pada periode saat mesin menyala dan diam. Konsumsi yang terkait dengan menghidupkan dan mematikan mesin adalah konsumsi untuk menghidupkan dan mematikannya sekali dikalikan dengan berapa kali mesin harus dihidupkan dan dimatikan. Konsumsi yang terkait dengan operasi pemrosesan adalah hasil kali konsumsi per satuan waktu dikalikan dengan waktu yang dihabiskan mesin untuk melakukan operasi pemrosesan. Waktu ini dipengaruhi oleh efek pembelajaran. Waktu idle mesin sesuai dengan jumlah interval antara pemrosesan operasi berurutan di mana diputuskan untuk tidak mematikan mesin.
Algoritma 2. Menyelesaikan solusi parsial dengan heuristik konstruktif yang rakus.
|
Algoritma 3. Diberikan perkiraan solusi terkini, mengembalikan tetangga terbaik dari suatu lingkungan berdasarkan penghapusan dan penyisipan kembali satu operasi.
 |
Algoritma 4. Membangun tetangga dari perkiraan solusi saat ini yang diperoleh dengan memasukkan kembali operasi yang dihapusvdirposisi mesink.
 |
Algoritma 5. Diberikan perkiraan solusi terkini, mengembalikan tetangga terbaik dari suatu lingkungan berdasarkan penghapusan satu operasi, penghancuran, penyisipan kembali, dan rekonstruksi.
 |
Algoritma 6. Operasi tak terjadwalvdan semua penerusnya di(V,A∪AM(Q))
 |
Algoritma 7. Strategi pencarian lokal berdasarkan lingkungan penyisipan ulang tunggal.
 |
Algoritma 8. Prosedur pencarian adaptif acak yang serakah
 |
Algoritma 9. Simulasi Anil
 |
Algoritma 10. Pencarian lingkungan variabel umum
 |
7.1 Eksperimen dengan strategi pencarian lokal
Bahasa Indonesia: Di bagian ini, kami menunjukkan hasil penerapan pencarian lokal GCH-LS-SRRN dan GCH-LS-SRDRR ke 150 instans berukuran besar yang dipertimbangkan. Rincian hasil yang diperoleh dengan menerapkan setiap metode ke setiap instans dapat ditemukan di (Birgin et al., 2024 , Tabel S2). Tabel 3 menunjukkan ringkasan hasilnya. Di tabel, kami menunjukkan konsumsi energi rata-rata dari solusi yang ditemukan oleh heuristik konstruktif GCH dan, untuk masing-masing dari dua pencarian lokal, konsumsi energi rata-rata dari solusi yang ditemukan, jumlah rata-rata iterasi, dan waktu CPU rata-rata dalam milidetik . Jumlah solusi terbaik yang ditemukan dan celah rata-rata ke solusi yang ditemukan oleh heuristik konstruktif GCH juga ditampilkan. GCH menghabiskan, rata-rata, 0,37 milidetik per instans dan tidak ada instans yang membutuhkan waktu lebih dari 2 milidetik.
| Contoh | GCH | GCH-LS-SRRN | GCH-LS-SRDRR | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Jenis | α | E¯ | #menang | gap¯(%) | E¯ | #it¯ | Time¯ | #menang | gap¯(%) | E¯ | #it¯ | Time¯ |
| DA | 0.1 | 1.245.668,07 | 6 | -6,21 | 1.157.385,23 | Tanggal 20.23 | 849.92 | 24 | -9,69 | 1.109.529,97 | 7.43 | 2.272,45 |
| 0.2 | 1.043.387,03 | 6 | -4,49 | 996.649,17 | Tanggal 17.10 | 723.87 | 24 | -8,29 | 950.481,00 | 6.60 | 2.045,01 dolar AS | |
| 0.3 | 906.801,00 | 3 | -4,65 | 864.704,50 | 15.27 | 540.29 | 27 | -9,63 | 818.844,27 | 6.77 | 2.027,10 | |
| kamu | 0.1 | 1.622.068,05 | 6 | -4.30 | 1.553.797,40 | Tanggal 20.35 | 8.745,91 | 14 | -9.11 | 1.487.848,90 | 6.35 | 6.333,98 |
| 0.2 | 1.436.712,65 | 3 | -4,97 | 1.370.043,95 | 20.60 | 9.280,43 | 17 | -9,38 | 1.315.247,10 | 6.05 | 4.791,40 | |
| 0.3 | 1.280.518,20 | 2 | -4,70 | 1.222.768,95 | pukul 20.40 | 8.266,10 | 18 | -9,25 | 1.174.502,65 | 6.95 | 7.043,83 | |
| Semua | 26 | -4,93 | 124 | -9,22 | ||||||||
Jelas bahwa iterasi GCH-LS-SRRN (pencarian di lingkungan sekitar) lebih murah daripada iterasi GCH-LS-SRDRR. Pada saat yang sama, GCH-LS-SRRN diharapkan melakukan lebih banyak iterasi daripada GCH-LS-SRDRR. Eksperimen mengonfirmasi bahwa yang pertama, rata-rata, melakukan sekitar tiga kali lebih banyak iterasi daripada yang terakhir. Namun, dalam contoh tipe DA, GCH-LS-SRRN membutuhkan waktu tiga kali lebih sedikit daripada yang terakhir, yang menunjukkan bahwa iterasi GCH-LS-SRRN adalah orde besaran lebih cepat. Hal yang sama tidak dikonfirmasi untuk contoh tipe Y. Dalam contoh tersebut, rasio antara jumlah iterasi dari dua pencarian lokal tetap sama, tetapi GCH-LS-SRDRR membutuhkan waktu lebih sedikit daripada LS-SRNN. Penjelasan untuk ini adalah tingkat fleksibilitas dan nonlinieritas rute dari dua jenis contoh. Instance dengan tipe disassemble assemble (DA) memiliki tingkat fleksibilitas yang lebih tinggi daripada instance dengan tipe Y dan itu membenarkan bahwa menghasilkan semua tetangga dari sebuah solusi lebih mahal. Secara keseluruhan, GCH-LS-SRRN meningkatkan solusi awal yang dibangun oleh heuristik konstruktif GCH sebesar 4,93% sementara GCH-LS-SRDRR meningkat sebesar 9,22%. GCH-LS-SRDRR juga lebih unggul daripada GCH-LS-SRRN dalam sejumlah solusi terbaik yang ditemukan. Waktu CPU yang digunakan oleh dua pencarian lokal menunjukkan bahwa instance dengan lebih dari 100 operasi mungkin menantang. Penerapan pencarian lokal, yang menggunakan teknik tetangga terbaik dan pada setiap iterasi memeriksa lingkungan lengkap dari solusi saat ini, sedikit menuntut dari sudut pandang biaya komputasi. Manakah dari dua pencarian lokal, atau lingkungan mereka, yang akan lebih baik ketika tertanam dalam konteks metaheuristik adalah sesuatu yang akan dianalisis di bagian berikutnya.
7.2 Eksperimen dengan metaheuristik
Rincian hasil yang diperoleh dengan menerapkan setiap metode pada setiap instans dapat ditemukan di Birgin et al. ( 2024 , Tabel S3–S5). Tabel 4 menunjukkan ringkasan hasil. Dalam tabel, kami menunjukkan konsumsi energi rata-rata saat mempertimbangkan rata-rata 10 kali pengujian per metode/instans, konsumsi energi rata-rata saat mempertimbangkan nilai terendah dari 10 kali pengujian per metode/instans, waktu CPU rata-rata (dalam detik) dengan mempertimbangkan waktu pengujian yang menemukan konsumsi energi terendah untuk setiap pasangan metode/instans. Jumlah solusi terbaik yang ditemukan dan celah rata-rata ke solusi yang ditemukan oleh heuristik konstruktif GCH juga ditampilkan. Dari total 150 instans, masing-masing metode GRASP-LS-SRRN, GRASP-LS-SRDRR, GVNS, SA-LS-SRRN, dan SA-LS-SRDRR menemukan solusi terbaik dalam 38, 52, 64, 0, dan 2 instans. Masing-masing metode meningkatkan solusi awal yang diberikan oleh heuristik konstruktif GCH masing-masing sebesar 12,43%, 11,51%, 11,92%, 2,97%, dan 10,59%. Gambar 4 menunjukkan evolusi konsumsi energi dari solusi yang dibangun oleh masing-masing metode sebagai fungsi waktu. Untuk memperkuat perbandingan antara metode, kami menggunakan uji Wilcoxon (Wilcoxon, 1945 ) untuk setiap pasangan metode, dengan tingkat signifikansi
untuk menerima atau menolak hipotesis nol bahwa “sampel dari kedua metode berasal dari distribusi yang sama” atau, dengan kata lain, “selisih antara sampel dari kedua metode mengikuti distribusi simetris di sekitar nol.” Tabel 5 menunjukkan hasilnya. Hal ini menunjukkan bahwa GVNS dan GRASP-LS-SRRN adalah setara. Lebih jauh, keduanya lebih baik daripada semua metode lain yang berbeda satu sama lain. GRASP-LS-SRDRR adalah metode terbaik ketiga, diikuti oleh SA-LS-SRDRR dan terakhir SA-LS-SRRN.
| Contoh | GRASP-LS-SRRN | GRASP-LS-SRDRR | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Jenis | α | #menang | gap¯(%) | E¯ | Emin¯ | Time¯ | #menang | gap¯(%) | E¯ | Emin¯ | Time¯ |
| DA | 0.1 | 7 | -12,71 | 1.089.544,74 | 1.077.181,30 | 275.11 | 6 | -11,84 | 1.095.389,50 | 1.087.000,47 | 205.18 |
| 0.2 | 7 | -11.40 | 935.288,63 | 924.574,67 | 276.96 | 6 | -10,31 | 945.413,83 | 936.549,37 | 202.52 | |
| 0.3 | 8 | -11,89 | 809.016,94 | 800.324,43 | 305.50 | 5 | -10,89 | 815.644,53 | 809.252,77 | 163.57 | |
| kamu | 0.1 | 4 | -13,34 | 1.445.083,76 | 1.427.460,25 | 310.04 | 11 | -12,61 | 1.457.253,89 | 1.450.942,15 | 200.66 |
| 0.2 | 4 | -13,01 | 1.283.622,88 | 1.269.477,20 | 276.27 | 12 | -12.15 | 1.297.485,71 | 1.291.717,60 | 212.16 | |
| 0.3 | 8 | -12,85 | 1.143.387,66 | 1.131.684,50 | 265.87 | 12 | -11,98 | 1.155.404,40 | 1.151.201,50 | 209.29 | |
| Semua | 38 | -12,43 | 52 | -11,51 | |||||||
| Contoh | GVNS | |||||
|---|---|---|---|---|---|---|
| Jenis | α | #menang | gap¯(%) | E¯ | Emin¯ | Time¯ |
| DA | 0.1 | 18 | -13,13 | 1.080.904,47 | 1.062.464,40 | 24.58 |
| 0.2 | 17 | -11,43 | 924.694,28 | 917.809,47 | 26.61 | |
| 0.3 | 16 | -11,81 | 802.414,55 | 796.975,97 | Tanggal 26.12 | |
| kamu | 0.1 | 6 | -12,23 | 1.447.009,73 | 1.434.069,70 | 46.56 |
| 0.2 | 4 | -11,38 | 1.289.193,43 | 1.281.924,55 | 42.25 | |
| 0.3 | 3 | -11.20 | 1.147.983,68 | 1.143.420,50 | 41.35 | |
| Semua | 64 | -11,92 | ||||
| SA-LS-SRRN | SA-LS-SRDRR | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Jenis | α | #menang | gap¯(%) | E¯ | Emin¯ | Time¯ | #menang | gap¯(%) | E¯ | Emin¯ | Time¯ |
| DA | 0.1 | angka 0 | -4,25 | 1.233.066,26 | 1.184.646,63 | 22.90 | angka 0 | -11,61 | 1.107.158,51 | 1.089.523,03 | 190.43 |
| 0.2 | angka 0 | -2,96 | 1.037.538,97 | 1.011.472,83 | 16.49 | 1 | -10,04 | 953.753,95 | 938.522,93 | 188.95 | |
| 0.3 | angka 0 | -3,75 | 900.615,48 | 878.058,83 | 19.98 | 1 | -10,53 | 826.519,04 | 812.194,93 | 163.53 | |
| kamu | 0.1 | angka 0 | -1,63 | 1.610.423,48 | 1.599.004,00 | 2.19 | angka 0 | -10,88 | 1.501.692,65 | 1.477.110,30 | Nomor telepon 133.30 |
| 0.2 | angka 0 | -2,38 | 1.425.396,49 | 1.406.635,35 | 4.79 | angka 0 | -10.45 | 1.338.861,23 | 1.312.209,35 | 107.78 | |
| 0.3 | angka 0 | -1,84 | 1.274.202,92 | 1.258.199,90 | 4.74 | angka 0 | -9,83 | 1.197.182,75 | 1.176.760,10 | 128.27 | |
| Semua | angka 0 | -2,97 | 2 | -10,59 | |||||||
| Perbandingan | R+ | R− | p-nilai | ||
|---|---|---|---|---|---|
| GRASP-LS-SRRN | melawan | GRASP-LS-SRDRR | 7.588 | 3.734 orang | 0,0003 |
| GRASP-LS-SRRN | melawan | GVNS | 5.361 orang | 5.964 orang | 0,5716 tahun |
| GRASP-LS-SRRN | melawan | SA-LS-SRRN | 11.325 | angka 0 | 0.0000 |
| GRASP-LS-SRRN | melawan | SA-LS-SRDRR | 11.275 | 50 | 0.0000 |
| GRASP-LS-SRDRR | melawan | GVNS | 4.329 tahun | 6.996 lembar | 0,0124 pukul 0,0124 |
| GRASP-LS-SRDRR | melawan | SA-LS-SRRN | 11.325 | angka 0 | 0.0000 |
| GRASP-LS-SRDRR | melawan | SA-LS-SRDRR | 10.540 | 785 | 0.0000 |
| GVNS | melawan | SA-LS-SRRN | 11.325 | angka 0 | 0.0000 |
| GVNS | melawan | SA-LS-SRDRR | 9.667 orang | 1.658 orang | 0.0000 |
| SA-LS-SRRN | melawan | SA-LS-SRDRR | angka 0 | 11.324 orang | 0.0000 |
Gambar 4 menunjukkan bahwa perbandingan antara metode-metode pada paragraf sebelumnya berlaku ketika mempertimbangkan batas waktu CPU 5 menit. Untuk batas waktu CPU yang lebih rendah, peringkat antara metode-metode, dalam hal konsumsi daya rata-rata, dapat bervariasi. Ketika kita membandingkan dua versi GRASP menggunakan pencarian lokal dengan lingkungan SRRN dan SRDRR, kita mengamati bahwa (i) untuk anggaran waktu kecil, mereka berperilaku serupa; (ii) untuk nilai-nilai antara anggaran waktu, intensitas lingkungan SRDRR mengarah pada solusi yang lebih baik secara rata-rata; dan (iii) untuk anggaran waktu yang lebih besar, lingkungan SRRN, yang lebih murah, memungkinkan metode untuk membuat diversifikasi yang lebih tinggi dengan melakukan lebih banyak pencarian lokal dari berbagai solusi awal dan yang mengarah, pada akhirnya, ke solusi yang lebih baik, secara rata-rata. Di sisi lain, GVNS tampaknya memanfaatkan kombinasi dari dua lingkungan yang ada dengan lebih baik dan mengungguli, ketika mengevaluasi konsumsi energi rata-rata, kedua versi GRASP. SA, dengan salah satu dari dua lingkungan, yang tidak menggunakan strategi pencarian lokal, tidak menyajikan kinerja yang kompetitif jika dibandingkan dengan metode lainnya.
7.3 Perbandingan dengan solusi dari metode solusi yang tepat
Dalam bagian ini, kami mempertimbangkan dua metaheuristik berkinerja terbaik (GVNS dan GRASP-LS-SRRN) dan menganalisis kinerjanya dengan mempertimbangkan solusi yang dihitung dengan metode yang tepat. Untuk percobaan ini, kami mempertimbangkan 50 contoh berukuran besar dari bagian sebelumnya, ditambah 60 contoh berukuran kecil yang diperkenalkan di Araujo et al. ( 2024b ), yang mana kami menyertakan data konsumsi energi dengan cara yang persis sama seperti untuk contoh berukuran besar (lihat uraian di awal Bagian 7 ). Untuk detail tentang karakteristik contoh berukuran kecil, lihat Birgin et al. ( 2024 , Tabel S12). Karena dalam percobaan ini, kami juga akan mempertimbangkan laju pembelajaran
; kita akan memiliki total 150 contoh berukuran besar dan 180 contoh berukuran kecil.
Model diselesaikan menggunakan IBM ILOG CPLEX Optimization Studio versi 22.1, menggunakan parameter default, dengan pustaka konser dan C++. Kode dikompilasi menggunakan g++ 10.2.1. Kami menyediakan solusi awal yang dihitung dengan heuristik konstruktif GCH (Algoritma 1 ). Solusi dilaporkan sebagai optimal oleh CPLEX ketika
Rincian solusi yang ditemukan oleh metaheuristik GVNS dan GRASP-LS-SRRN saat diterapkan pada instans berukuran kecil tersedia di Birgin et al. ( 2024 , Tabel S16–S18). Heuristik digunakan dengan parameter yang dikalibrasi untuk instans berukuran besar. Artinya, heuristik tidak dikalibrasi ulang. Karena ini adalah metode komponen acak, setiap metode diterapkan 10 kali pada setiap instans. Saat membandingkan solusi yang ditemukan oleh metaheuristik dengan solusi yang ditemukan oleh CPLEX, kami mempertimbangkan (a) rata-rata dari 10 kali pengujian dan (b) minimum dari 10 kali pengujian. Dalam setiap kasus, kami menghitung celah relatif terhadap solusi yang ditemukan oleh CPLEX. Mari kita pertimbangkan kasus (b) terlebih dahulu.
Jika kita hanya mempertimbangkan 137 contoh berukuran kecil di mana CPLEX menemukan solusi optimal yang terbukti, GVNS menemukan solusi yang, rata-rata, berjarak 2,02% dari solusi optimal, sedangkan angka ini adalah 0,22% untuk GRASP-LS-SRRN. Jika kita mempertimbangkan semua 180 contoh berukuran kecil, nilai-nilai ini masing-masing adalah 2,16% dan 0,02%. Dalam satu-satunya contoh berukuran besar di mana CPLEX menemukan solusi optimal yang terbukti, metaheuristik GVNS dan GRASP-LS-SRRN menemukan solusi dengan celah masing-masing 3,98% dan 0,09%. Mempertimbangkan semua 150 contoh berukuran besar, metaheuristik GVNS dan GRASP-LS-SRRN menemukan solusi dengan celah rata-rata masing-masing -8,70% dan -9,32%. Bila kita mempertimbangkan kasus (a), yaitu, rata-rata dari 10 kali percobaan untuk setiap metode/instans, keempat nilai yang sama untuk instans berukuran kecil adalah 2,16%, 0,24%, 2,29%, dan 0,04%, sedangkan untuk instans berukuran besar adalah 4,50%, 0,09%, -8,00%, dan -8,42%, yaitu, variasi yang signifikannya kecil. Data yang paling relevan dari percobaan ini adalah bahwa GRASP-LS-SRRN menemukan solusi pada, rata-rata, 0,22% dari 137 optima yang diketahui dan, bila kita menyertakan 43 instans dengan optima yang diketahui yang tidak terjamin, selisih rata-ratanya adalah 0,02%.
8 Penutup
Dalam karya ini, kami mempertimbangkan lingkungan jobshop yang fleksibel dengan dua fitur khusus: rute nonlinier (atau prioritas antara operasi pekerjaan yang sama yang diberikan oleh grafik asiklik yang diarahkan secara sewenang-wenang) dan efek pembelajaran pada waktu pemrosesan. Sejalan dengan masalah keberlanjutan kontemporer, kami mempertimbangkan minimalisasi konsumsi energi. Kami merumuskan masalah tersebut sebagai masalah MILP. Kami mengusulkan heuristik konstruktif, dua lingkungan, dan tiga metaheuristik. Kami melakukan eksperimen komprehensif untuk menunjukkan kemanjuran metode yang dipelajari. GVNS yang menggunakan dua lingkungan secara bersamaan adalah yang paling efektif dalam contoh berukuran besar. Dalam contoh berukuran kecil, GRASP dengan lingkungan pelepasan dan pemasangan kembali adalah yang paling efektif. Ia menemukan solusi yang, rata-rata, 0,22% dari solusi optimal yang diketahui.
Dalam pekerjaan mendatang, kami bermaksud mempertimbangkan lingkungan FJS dengan rute nonlinier dan, alih-alih konsumsi energi, total biaya energi. Ini berarti mempertimbangkan biaya energi yang bervariasi dari waktu ke waktu, termasuk pertimbangan waktu puncak dan tarif musiman atau tarif listrik berdasarkan waktu penggunaan. (Lihat Shen et al., 2023 , dan referensi di dalamnya untuk detailnya.) Kemungkinan lain yang membawa masalah yang sedang dipertimbangkan lebih dekat ke kenyataan adalah dengan mempertimbangkan bahwa sebuah mesin dapat beroperasi pada kecepatan yang berbeda dan bahwa konsumsi energinya bergantung pada kecepatannya. (Lihat Wu dan Sun, 2018. ) Model pembelajaran alternatif untuk yang dipertimbangkan dalam pekerjaan saat ini serta model penurunan, ditinjau oleh Pei et al. ( 2022 ). Menganalisis berbagai model pembelajaran serta memasukkan pengaruh penurunan dalam konteks masalah yang dipelajari adalah tugas yang mungkin untuk pekerjaan mendatang.
