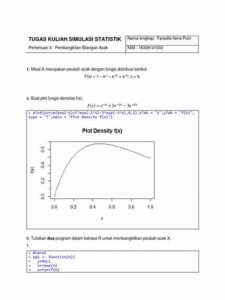
ABSTRAK
Hubungan antara dua variabel yang diukur beberapa kali per individu sering dievaluasi dalam studi klinis. Data ini tidak independen; oleh karena itu, koefisien korelasi Pearson tidak tepat, dan beberapa koefisien korelasi untuk data ini telah diusulkan. Namun, jika ada data yang hilang, metode yang ada dapat menjadi bias. Dalam artikel ini, kami mengusulkan koefisien korelasi pengukuran berulang tertimbang yang memberikan estimasi akurat, bahkan dengan data yang hilang, dalam studi di mana partisipan idealnya memiliki jumlah pengukuran yang sama. Kami juga menyediakan interval kepercayaan bootstrap untuk koefisien korelasi pengukuran berulang tertimbang. Kami mengevaluasi kinerja metode yang diusulkan dan yang ada (yaitu, koefisien korelasi Pearson sederhana, koefisien korelasi Pearson untuk rata-rata, rata-rata koefisien korelasi Pearson, koefisien korelasi berdasarkan analisis kovarians, dan koefisien korelasi berdasarkan model efek campuran linier) melalui simulasi dan aplikasi pada data aktual. Dalam evaluasi numerik menggunakan simulasi, metode yang diusulkan secara konsisten mengungguli metode yang ada. Kami merekomendasikan penggunaan koefisien korelasi pengukuran berulang tertimbang untuk menangani nilai yang hilang dalam data pengukuran ganda.
Singkatan
ANCOVA
analisis kovariansi
BSS
sistem pemantauan tanda vital sensor tempat tidur
CI
interval kepercayaan
TA-BSS
amplitudo pasang surut yang berhubungan dengan pernapasan oleh sistem pemantauan tanda-tanda vital sensor tempat tidur
TV-PN
volume tidal oleh ventilator pneumotachograph
1 Pendahuluan
Koefisien korelasi Pearson adalah indikator terkenal untuk mengevaluasi hubungan antara dua variabel untuk data independen [ 1 ] dan sesuai ketika setiap partisipan hanya memiliki satu pasang data. Namun, ini tidak memadai untuk data dengan dua atau lebih pasang pengukuran per partisipan. Penelitian sebelumnya telah menyelidiki koefisien korelasi untuk data non-independen tersebut [ 2 ]. Dua koefisien korelasi utama untuk beberapa pasang data telah diusulkan: satu berdasarkan analisis kovariansi (ANCOVA) [ 3 – 5 ] dan yang lainnya berdasarkan model efek campuran linier [ 6 – 8 ]. Metode-metode ini memperkirakan koefisien korelasi dengan menyesuaikan variabilitas antarindividu atau efek tingkat individu. Dalam penelitian medis, koefisien korelasi ini telah diterapkan pada penelitian dengan pemantauan berkelanjutan [ 9 – 14 ]. Koefisien korelasi intrakelas sering digunakan dalam uji reliabilitas dengan beberapa pasang data [ 15 ]. Namun, koefisien korelasi intrakelas untuk pengukuran berulang mengasumsikan bahwa nilai sebenarnya dari pengukuran adalah konstan pada titik waktu yang berbeda.
Ketika memperkirakan hubungan antara dua variabel, partisipan harus dipertimbangkan secara setara dalam penelitian klinis yang ideal. Estimasi adalah rata-rata individu dari korelasi dua variabel pada satu titik waktu dalam populasi target. Situasi di mana satu partisipan memiliki data pengukuran beberapa kali lebih banyak daripada partisipan lain tidaklah masuk akal dalam situasi yang umum. Namun, dalam studi klinis dengan pengukuran berulang, jumlah data pengukuran yang diamati tidak selalu sama di antara partisipan. Ketika partisipan menjalani jumlah pengukuran yang berbeda, koefisien korelasi Pearson dan koefisien korelasi yang ada untuk data pengukuran berulang dapat secara tidak proporsional mencerminkan fitur partisipan dengan lebih banyak data karena metode ini tidak menyesuaikan jumlah pengukuran per partisipan. Dalam studi di mana jumlah pengukuran yang sama idealnya direncanakan untuk setiap individu, variasi dalam jumlah pengukuran dapat dianggap sebagai masalah data yang hilang. Meskipun perbedaan dalam jumlah pengukuran dapat menimbulkan bias, pengaruh data yang hilang pada koefisien korelasi dengan pengukuran berulang belum diselidiki secara memadai.
Kami mengusulkan koefisien korelasi pengukuran berulang tertimbang, koefisien korelasi baru untuk data pengukuran berulang yang menangani bias tergantung pada variasi jumlah pengukuran. Kami menambahkan operasi perataan untuk setiap individu dalam estimasi ke koefisien korelasi yang ada berdasarkan ANCOVA untuk menyamakan tingkat dampak individu pada penaksir. Kami juga menyediakan interval keyakinan bootstrap untuk koefisien korelasi pengukuran berulang tertimbang. Dalam studi ini, kami mengevaluasi kinerja koefisien korelasi berdasarkan koefisien korelasi Pearson, koefisien korelasi yang ada untuk data pengukuran berulang, dan koefisien korelasi pengukuran berulang tertimbang di bawah kondisi data yang hilang dan tidak hilang.
2 Koefisien Korelasi untuk Data Pengukuran Berulang

2.1 Metode Berdasarkan Koefisien Korelasi Pearson

2.2 Koefisien Korelasi Berdasarkan ANCOVA

2.3 Koefisien Korelasi Berdasarkan Model Efek Campuran Linier

2.4 Koefisien Korelasi Pengukuran Berulang Tertimbang

2.5 Interval Kepercayaan

3 Studi Simulasi
3.1 Pembuatan Data


| Skenario 1 | Skenario 2 | Skenario 3 | Skenario 4 | |
|---|---|---|---|---|
| μ1x | angka 0 | 1 | angka 0 | 1 |
| σ1x | 1 | 1 | 1 | 1 |
| μ1y | angka 0 | 1 | angka 0 | 1 |
| σ1y | 1 | 1 | 1 | 1 |
| r1 | 0.8 | 0.8 | 0.8 | 0.8 |
| E[pk=1] | 0.3 | 0.3 | 0.1 | 0.1 |
| μ2x | angka 0 | angka 0 | angka 0 | angka 0 |
| σ2x | 1 | 1 | 1 | 1 |
| μ2y | angka 0 | angka 0 | angka 0 | angka 0 |
| σ2y | 1 | 1 | 1 | 1 |
| r2 | 0.4 | 0.4 | 0.4 | 0.4 |
| E[pk=2] | 0.3 | 0.3 | 0.5 | 0.5 |

| Metode korelasi | Skenario 1 | Skenario 2 | Skenario 3 | Skenario 4 | |
|---|---|---|---|---|---|
| Data lengkap | rP | 0,60 (0,039) | 0,68 (0,032) | 0,60 (0,039) | 0,68 (0,032) |
| rPA | 0,60 (0,128) | 0,89 (0,036) | 0,60 (0,128) | 0,89 (0,036) | |
| rAP | 0,58 (0,041) | 0,58 (0,041) | 0,58 (0,041) | 0,58 (0,041) | |
| rAN | 0,60 (0,040) | 0,60 (0,040) | 0,60 (0,040) | 0,60 (0,040) | |
| rLM | 0,60 (0,040) | 0,60 (0,040) | 0,60 (0,040) | 0,60 (0,040) | |
| rW | 0,60 (0,040) | 0,60 (0,040) | 0,60 (0,040) | 0,60 (0,040) | |
| Data hilang | rP | 0,60 (0,048) | 0,68 (0,040) | 0,66 (0,044) | 0,72 (0,036) |
| rPA | 0,59 (0,152) | 0,84 (0,064) | 0,52 (0,184) | 0,80 (0,087) | |
| rAP | 0,56 (0,064) | 0,56 (0,064) | 0,57 (0,075) | 0,57 (0,075) | |
| rAN | 0,60 (0,052) | 0,60 (0,052) | 0,67 (0,047) | 0,67 (0,047) | |
| rLM | 0,60 (0,051) | 0,60 (0,051) | 0,66 (0,047) | 0,66 (0,047) | |
| rW | 0,60 (0,054) | 0,60 (0,054) | 0,62 (0,060) | 0,62 (0,060) | |
Catatan: Perkiraan rata-rata 0,6 disorot dalam huruf tebal .
| Metode korelasi | Skenario 1 | Skenario 2 | Skenario 3 | Skenario 4 | |
|---|---|---|---|---|---|
| Data lengkap | rP | 0,60 (0,017) | 0,68 (0,015) | 0,60 (0,017) | 0,68 (0,015) |
| rPA | 0,60 (0,127) | 0,97 (0,009) | 0,60 (0,127) | 0,97 (0,009) | |
| rAP | 0,60 (0,017) | 0,60 (0,017) | 0,60 (0,017) | 0,60 (0,017) | |
| rAN | 0,60 (0,018) | 0,60 (0,018) | 0,60 (0,018) | 0,60 (0,018) | |
| rLM | 0,60 (0,018) | 0,60 (0,018) | 0,60 (0,018) | 0,60 (0,018) | |
| rW | 0,60 (0,018) | 0,60 (0,018) | 0,60 (0,018) | 0,60 (0,018) | |
| Data hilang | rP | 0,60 (0,024) | 0,68 (0,020) | 0,66 (0,022) | 0,72 (0,017) |
| rPA | 0,59 (0,145) | 0,96 (0,018) | 0,53 (0,188) | 0,94 (0,032) | |
| rAP | 0,59 (0,023) | 0,59 (0,023) | 0,59 (0,029) | 0,59 (0,029) | |
| rAN | 0,60 (0,024) | 0,60 (0,024) | 0,66 (0,022) | 0,66 (0,022) | |
| rLM | 0,60 (0,024) | 0,60 (0,024) | 0,66 (0,022) | 0,66 (0,022) | |
| rW | 0,60 (0,023) | 0,60 (0,023) | 0,60 (0,027) | 0,60 (0,027) | |
Catatan: Perkiraan rata-rata 0,6 disorot dalam huruf tebal .
| Metode korelasi | Skenario 1 | Skenario 2 | Skenario 3 | Skenario 4 | |
|---|---|---|---|---|---|
| Data lengkap | rP | 0,60 (0,012) | 0,68 (0,010) | 0,60 (0,012) | 0,68 (0,010) |
| rPA | 0,59 (0,128) | 0,99 (0,004) | 0,59 (0,128) | 0,99 (0,004) | |
| rAP | 0,60 (0,012) | 0,60 (0,012) | 0,60 (0,012) | 0,60 (0,012) | |
| rAN | 0,60 (0,013) | 0,60 (0,013) | 0,60 (0,013) | 0,60 (0,013) | |
| rLM | 0,60 (0,013) | 0,60 (0,013) | 0,60 (0,013) | 0,60 (0,013) | |
| rW | 0,60 (0,013) | 0,60 (0,013) | 0,60 (0,013) | 0,60 (0,013) | |
| Data hilang | rP | 0,60 (0,019) | 0,68 (0,015) | 0,66 (0,017) | 0,72 (0,013) |
| rPA | 0,59 (0,145) | 0,98 (0,009) | 0,53 (0,186) | 0,97 (0,018) | |
| rAP | 0,60 (0,016) | 0,60 (0,016) | 0,60 (0,020) | 0,60 (0,020) | |
| rAN | 0,60 (0,019) | 0,60 (0,019) | 0,66 (0,017) | 0,66 (0,017) | |
| rLM | 0,60 (0,019) | 0,60 (0,019) | 0,66 (0,017) | 0,66 (0,017) | |
| rW | 0,60 (0,016) | 0,60 (0,016) | 0,60 (0,020) | 0,60 (0,020) | |
Catatan: Perkiraan rata-rata 0,6 disorot dalam huruf tebal .
| Metode korelasi | Skenario 1 | Skenario 2 | Skenario 3 | Skenario 4 | |
|---|---|---|---|---|---|
| Data lengkap | rAN | 95,3% | 95,3% | 95,3% | 95,3% |
| rW | 95,3% | 95,3% | 95,3% | 95,3% | |
| Data hilang | rAN | 90,4% | 90,4% | 16,8% | 16,8% |
| rW | 93,7% | 93,7% | 93,7% | 93,7% |
| Metode korelasi | Skenario 1 | Skenario 2 | Skenario 3 | Skenario 4 | |
|---|---|---|---|---|---|
| Data lengkap | rAN | 0,069 tahun | 0,069 tahun | 0,069 tahun | 0,069 tahun |
| rW | 0,069 tahun | 0,069 tahun | 0,069 tahun | 0,069 tahun | |
| Data hilang | rAN | 0,082 | 0,082 | 0,079 tahun | 0,073 tahun |
| rW | 0,087 tahun | 0,087 tahun | 0,099 tahun | 0,099 tahun |
4 Studi Aplikasi
4.1 Sistem Pemantauan Tanda Vital dengan Sensor Tempat Tidur di ICU
Kami menerapkan metode kami untuk mempelajari penilaian laju dan volume pernapasan bebas kontak menggunakan sel beban di bawah kaki tempat tidur (UMIN-CTR: UMIN000047793) [ 17 ]. Sistem Pemantauan Tanda Vital (BSS) Sensor Tempat Tidur dikembangkan sebagai sistem pemantauan tanpa kendala untuk mengukur amplitudo pasang surut terkait pernapasan dan laju pernapasan menggunakan data dari sel beban di keempat kaki tempat tidur. Studi ini menilai korelasi antara amplitudo pasang surut terkait pernapasan oleh BSS (TA-BSS) dan volume pasang surut oleh ventilator pneumotachograph (TV-PN) pada 14 pasien dengan ventilasi mekanis di ICU. Pasien yang memberikan persetujuan dan memiliki data yang tersedia setidaknya selama 24 jam disertakan. Data terkait pernapasan dicatat sebagai satu pengukuran setiap 10 menit. Pengukuran dilakukan pada 288 titik waktu untuk 13 subjek dan 248 titik waktu untuk satu subjek. Peluang hilang rata-rata adalah 11,6%, dengan rentang interkuartil 4,9% hingga 22,9%.
4.2 Metode Statistik
Kami menerapkan koefisien korelasi yang dipertimbangkan dalam studi simulasi untuk menilai hubungan antara TA-BSS dan TV-PN dengan data dari studi ini. Awalnya, kami mencoba menerapkan metode korelasi pada keseluruhan data; namun, metode yang didasarkan pada model efek campuran tidak dapat memperoleh solusi konvergensi. Akibatnya, kami memperkirakan estimasi titik menggunakan metode selain model efek campuran untuk keseluruhan data.
Kami juga menerapkan metode korelasi pada himpunan data subsampel, dengan pengambilan sampel acak 50 titik data per partisipan tanpa penggantian. Median probabilitas hilang dalam himpunan data subsampel adalah 14,0%, dengan rentang interkuartil 4,0% hingga 32,0%. Estimasi titik dan interval kepercayaan (CI) 95% diestimasi menggunakan metode bootstrap. Dalam analisis post hoc, kami mengecualikan satu partisipan dengan koefisien korelasi Pearson negatif dan menilai ulang korelasinya.
5 Hasil

| Metode korelasi | Data keseluruhan | Data sampel | |
|---|---|---|---|
| Memperkirakan | Memperkirakan | 95% CI | |
| rP | 0,593 tahun | 0,566 tahun | [0,518, 0,612] |
| rPA | 0.622 | 0,593 tahun | [0,535, 0,645] |
| rAP | 0,360 | 0,385 | [0,320, 0,463] |
| rAN | 0.552 | 0,544 tahun | [0,486, 0,605] |
| rLM | Bahasa Indonesia | 0,544 tahun | [0,485, 0,605] sebuah |
| rW | 0,551 tahun | 0,537 tahun | [0,477, 0,598] |
Singkatan: CI, interval kepercayaan; TA-BSS, amplitudo pasang surut oleh sistem pemantauan tanda-tanda vital sensor tempat tidur; TV-PN, volume pasang surut oleh pneumotakograf ventilator. a Perkiraan hanya diperoleh 656 kali saat bootstrapping.
| Metode korelasi | 13 data | 14 data | Perbedaan |
|---|---|---|---|
| rP | 0.603 | 0,566 tahun | 0,037 hari |
| rPA | 0,635 tahun | 0,593 tahun | 0,042 tahun |
| rAP | 0.444 | 0,385 | 0,059 tahun |
| rAN | 0.553 | 0,544 tahun | 0,009 |
| rLM | 0.553 | 0,544 tahun | 0,009 |
| rW | 0,544 tahun | 0,537 tahun | 0,007 tahun |
Singkatan: TA-BSS, amplitudo pasang surut oleh sistem pemantauan tanda-tanda vital sensor tempat tidur; TV-PN, volume pasang surut oleh pneumotachograph ventilator.
6 Diskusi
Koefisien korelasi untuk data pengukuran berulang yang tidak independen, di mana koefisien korelasi Pearson tidak sesuai, telah diusulkan. Namun, dalam metode ini, perbedaan jumlah pengukuran per partisipan tidak disesuaikan dan ini dapat menimbulkan bias dalam estimasi. Dalam studi ini, kami mengevaluasi kinerja koefisien korelasi yang ada untuk data pengukuran berulang dengan dan tanpa data yang hilang dalam studi simulasi dan mengusulkan koefisien korelasi pengukuran berulang tertimbang untuk menangani variasi jumlah pengukuran. Setelah simulasi, metode ini diterapkan pada data aktual untuk mengevaluasi hubungan antara TA-BSS dan TV-PN.
Dalam simulasi kami, ketika data yang hilang tidak bergantung pada variabel lain, metode yang diusulkan dan koefisien korelasi berdasarkan ANCOVA dan model efek campuran menunjukkan bias minimal. Namun, dalam skenario di mana probabilitas yang hilang dan korelasi saling terkait, koefisien korelasi berdasarkan ANCOVA dan model efek campuran sama-sama ditaksir terlalu tinggi. Namun, metode yang diusulkan menghasilkan bias yang dapat diabaikan.
Kami mengungkapkan bahwa interval keyakinan yang diusulkan valid dengan dan tanpa data yang hilang. Melalui simulasi, kami mengonfirmasi bahwa proporsi cakupan interval keyakinan yang diusulkan adalah sekitar 95%. Metode yang diusulkan menunjukkan interval keyakinan 95% yang lebih lebar daripada metode yang ada, tetapi interval keyakinan berdasarkan ANCOVA menunjukkan kemungkinan sifat cakupan yang kurang di bawah data yang hilang. Ini menunjukkan bahwa lebar interval keyakinan dari metode yang ada diremehkan. Ketika tidak ada data yang hilang (yaitu, jumlah titik waktu sama untuk semua peserta), metode yang diusulkan menghasilkan nilai yang sama dengan koefisien korelasi berdasarkan ANCOVA.
Metode yang berdasarkan koefisien korelasi Pearson hanya masuk akal hanya dalam situasi tertentu, bahkan tanpa data yang hilang. Seperti yang diharapkan, ketika memperkirakan koefisien korelasi Pearson dari seluruh dataset tanpa mempertimbangkan pengukuran berulang, atau ketika memperkirakan koefisien korelasi Pearson untuk nilai rata-rata untuk setiap peserta, penaksir ini tidak valid. Hasil ini konsisten dengan penelitian sebelumnya [ 2 , 5 ]. Koefisien korelasi Pearson rata-rata untuk setiap peserta diremehkan.
ketika jumlah titik waktu kecil. Koefisien korelasi Pearson yang diestimasi dari sampel bukanlah penduga yang tidak bias, dan perkiraannya
diketahui, dimana
adalah koefisien korelasi yang diperkirakan dari sampel dan
adalah koefisien korelasi untuk populasi [ 18 , 19 ]. Hubungan ini dapat menjelaskan perkiraan yang terlalu rendah ini. Ketika jumlah titik waktu mencukupi, yaitu 50 atau lebih, koefisien korelasi Pearson rata-rata merupakan penduga yang dapat diterima, bahkan dengan data yang hilang.
Kami menerapkan metode ini pada data aktual untuk mengevaluasi hubungan antara TA-BSS dan TV-PN. Seperti hasil untuk
Bahasa Indonesia:
, Dan
hampir sama, pengaruh data yang hilang dianggap kecil, dan korelasinya sekitar 0,54. Meskipun jumlah titik waktu cukup, estimasi
kurang dari 0,54. Analisis sensitivitas, dengan mengecualikan satu partisipan dengan koefisien korelasi Pearson negatif, menunjukkan bahwa perubahan
lebih besar dari itu di
Bahasa Indonesia:
, Dan
Meskipun diperlukan penelitian lebih lanjut, hasil penelitian menunjukkan bahwa
mungkin tidak memberikan estimasi yang stabil dalam situasi di mana ukuran sampelnya kecil dan mencakup outlier.
Bila diterapkan pada keseluruhan data aktual,
tidak dapat memberikan solusi konvergen. Dalam simulasi kami, koefisien korelasi berdasarkan model efek campuran tidak konvergen hingga 20,2% dari waktu. Dalam analisis kami, kami mengasumsikan simetri gabungan dalam struktur antara titik waktu; namun, masalah konvergensi muncul. Dalam studi dengan banyak pengukuran, seperti studi kesehatan digital [ 20 , 21 ], metode berdasarkan model efek campuran mungkin tidak sesuai karena masalah volume komputasi dan konvergensi.
Konsep operasi rata-rata dari metode yang kami usulkan mirip dengan ukuran klaster informatif dalam uji coba acak klaster. Bias akibat data yang hilang dalam penelitian kami disebut sebagai perbedaan estimasi untuk efek perlakuan rata-rata partisipan dan efek perlakuan rata-rata klaster dalam uji coba acak klaster [ 22 – 24 ]. Saat memperkirakan koefisien korelasi dari pengukuran berulang, memperhatikan estimasi sangatlah penting. Seperti disebutkan dalam bagian Metode, estimasi koefisien korelasi Pearson dan koefisien korelasi pengukuran berulang berbeda. Selain itu, perbedaan antara data ideal dan data aktual harus dipahami secara memadai, dan seseorang harus memilih estimator yang tepat untuk tujuan penelitian dalam pengaturan praktis.
Studi kami memiliki beberapa keterbatasan dan area untuk penelitian di masa mendatang. Pertama, metode yang diusulkan mengasumsikan independensi dalam diri partisipan; namun, kami tidak mengevaluasi kinerja ketika asumsi ini tidak valid. Mengasumsikan independensi kesalahan pengukuran dalam diri partisipan dapat menjadi hal yang wajar dalam pengaturan di mana data diukur pada beberapa titik waktu dalam waktu singkat. Namun, ketika memperkirakan koefisien korelasi untuk data pengukuran berulang yang diikuti selama berbulan-bulan atau bertahun-tahun, kami mungkin perlu mempertimbangkan struktur varians kesalahan yang tidak independen. Hanya koefisien korelasi berdasarkan model efek campuran yang dapat menggabungkan struktur varians kompleks. Namun, model efek campuran juga akan menjadi tantangan ketika jumlah titik waktu besar, atau ketika mengasumsikan struktur yang seragam di antara partisipan tidak masuk akal karena jumlah titik waktu berbeda. Mengevaluasi koefisien korelasi dalam situasi ini merupakan topik untuk penelitian di masa mendatang. Kedua, efisiensi metode yang diusulkan dan estimasi interval kepercayaan masih memerlukan eksplorasi lebih lanjut. Dalam studi ini, kami belum menunjukkan varians teoritis dan interval kepercayaan metode yang diusulkan. Mungkin ada pembobotan yang lebih baik yang akan mengurangi varians karena kami mengusulkan untuk koefisien korelasi yang tidak bias, bukan untuk mencapai varians minimum dari estimator. Pekerjaan teoritis untuk mengklarifikasi distribusi dan varians dari estimator yang telah kami usulkan dan membahas bobot optimal adalah salah satu topik penelitian di masa depan. Isu-isu ini dapat memberikan dasar untuk membangun interval kepercayaan yang lebih baik dan membahas perhitungan ukuran sampel. Interval kepercayaan untuk koefisien korelasi untuk data pengukuran berulang sering diperkirakan menggunakan metode bootstrap [ 5 , 25 ], yang juga kami gunakan untuk memperkirakan interval kepercayaan untuk koefisien korelasi pengukuran berulang yang tertimbang. Kami menekankan bahwa estimator yang diusulkan dan yang ada memberikan nilai yang sama ketika jumlah pengukuran yang diamati untuk setiap peserta adalah sama. Ketika ada variasi dalam jumlah pengukuran, metode yang diusulkan menunjukkan interval kepercayaan yang sedikit lebih lebar daripada metode yang ada. Namun, interval kepercayaan berdasarkan metode bootstrap dapat memberikan kinerja yang memadai untuk studi klinis dan epidemiologi, dan hasil ini tidak serta merta menunjukkan bahwa estimator yang ada akan lebih unggul dalam efisiensi karena probabilitas cakupan estimator yang ada di bawah 95%.
Sebagai kesimpulan, kami mengusulkan koefisien korelasi pengukuran berulang tertimbang dan mengevaluasi kinerja berbagai koefisien korelasi untuk data pengukuran berulang dalam kondisi dengan dan tanpa data yang hilang. Metode yang ada tidak dapat memperkirakan koefisien korelasi yang valid dalam beberapa situasi, tergantung pada jumlah titik waktu, nilai variabel yang diharapkan, dan mekanisme data yang hilang. Sebaliknya, metode yang diusulkan secara konsisten memberikan estimasi yang valid. Oleh karena itu, kami merekomendasikan penggunaan koefisien korelasi pengukuran berulang tertimbang untuk beberapa titik data dengan nilai yang hilang.