ABSTRAK
Waktu untuk suatu peristiwa yang menarik sepanjang hidup adalah ukuran utama manfaat klinis dari suatu intervensi yang digunakan dalam penilaian teknologi kesehatan (HTA). Dalam uji coba yang sama, beberapa titik akhir juga dapat dipertimbangkan. Misalnya, waktu bertahan hidup secara keseluruhan dan bebas perkembangan untuk berbagai obat dalam studi onkologi. Tantangan umum adalah ketika suatu intervensi hanya efektif untuk sebagian dari populasi yang tidak dapat diidentifikasi secara klinis. Oleh karena itu, keanggotaan kelompok laten serta model bertahan hidup terpisah untuk kelompok yang teridentifikasi perlu diperkirakan. Namun, tindak lanjut dalam uji coba mungkin relatif singkat yang menyebabkan penyensoran yang substansial. Kami menyajikan kerangka hierarki Bayesian umum yang dapat menangani kompleksitas ini dengan memanfaatkan kesamaan fraksi penyembuhan antara titik akhir; memperhitungkan korelasi antara mereka dan meningkatkan ekstrapolasi di luar data yang diamati. Dengan asumsi pertukaran antara fraksi penyembuhan memfasilitasi peminjaman informasi antara titik akhir. Kami melakukan studi simulasi yang komprehensif untuk mengevaluasi kinerja model dalam skenario yang berbeda. Kami juga menunjukkan manfaat penggunaan pendekatan kami dengan contoh yang memotivasi, uji coba fase 3 CheckMate 067 yang terdiri dari pasien dengan melanoma metastasis yang diobati dengan terapi lini pertama.
Singkatan
MCM
model penyembuhan campuran
1 Pendahuluan
Intervensi yang memengaruhi waktu terjadinya suatu peristiwa yang menarik, seperti perkembangan penyakit atau kematian dalam uji kanker, merupakan bagian besar dari penilaian oleh lembaga Penilaian Teknologi Kesehatan (HTA), seperti Institut Nasional untuk Keunggulan Kesehatan dan Perawatan (NICE), di Inggris [ 1 ]. Misalnya, intervensi baru mungkin diharapkan dapat meningkatkan jumlah waktu hingga pasien mengalami perkembangan penyakit atau kematian karena penyebab apa pun. Oleh karena itu, ‘data kelangsungan hidup’ berperan penting dalam pemodelan dalam HTA [ 2 , 3 ].
Fitur data survival dari uji klinis adalah bahwa data tersebut sering dilaporkan selama dan di akhir periode uji klinis. Hal ini memungkinkan penilaian berkelanjutan dan dapat menginformasikan keputusan seperti penghentian awal uji klinis karena bahaya atau kesia-siaan. Namun, pada kenyataannya, biasanya tidak mungkin untuk memanfaatkan data yang dikumpulkan secara real time karena ada periode di mana data tersebut perlu dibersihkan karena masalah, seperti data yang hilang dan kesalahan kualitas data lainnya. Oleh karena itu, snapshot data uji klinis dibuat pada titik-titik yang telah ditentukan sebelumnya yang didefinisikan dalam protokol studi. Ini dapat dilakukan pada tanggal tertentu, waktu tindak lanjut, atau sejumlah pasien tertentu. Subset data survival yang dibuat pada waktu-waktu tertentu disebut pemotongan data .
Untuk mengukur secara akurat manfaat kesehatan dan ekonomi dari intervensi baru menggunakan data survival tersebut, perlu untuk memperkirakan mean survival time , yaitu, efek jangka panjang dari intervensi tertentu. Ini berbeda dengan ringkasan kurva survival umum, seperti median time, yang biasanya digunakan dalam analisis ‘biostatistik’ standar. Keunikan ini memiliki implikasi penting karena, untuk menghitung mean survival time, kita memerlukan kurva survival penuh, yaitu, selama masa hidup pasien, tetapi data yang tersedia (misalnya, pemotongan data dari uji coba acak) hampir pasti hanya mencakup kerangka waktu terbatas dan tunduk pada tingkat penyensoran yang tinggi. Dengan demikian, perlu untuk mengekstrapolasi kurva survival yang diamati ke cakrawala waktu yang biasanya jauh lebih lama daripada yang dipertimbangkan dalam studi eksperimental. Oleh karena itu, tidak seperti analisis waktu-ke-peristiwa ‘standar’ yang sering didasarkan pada model semi-parametrik (misalnya, regresi Cox), pemodelan HTA didasarkan pada pendekatan parametrik penuh terhadap analisis kelangsungan hidup, seperti yang direkomendasikan oleh Dokumen Dukungan Teknis (TSD) Unit Pendukung Keputusan (DSU) NICE yang sangat berpengaruh [ 1 ].
Fitur penting lain dari data survival di bidang penelitian kanker telah muncul dalam dekade terakhir karena pengembangan pengobatan imuno-onkologi yang berpotensi sangat berhasil. Ini bertujuan untuk merangsang sistem imun tubuh untuk mengenali dan membunuh sel kanker [ 4 ]. Beberapa jenis imunoterapi dapat digunakan untuk mengobati melanoma termasuk inhibitor titik pemeriksaan imun, interleukin-2 (IL-2), dan terapi virus onkolitik. Secara khusus, terapi kombinasi blokade titik pemeriksaan imun penghambat telah menunjukkan keberhasilan yang signifikan dalam meningkatkan respons imun terhadap kanker dan dapat menghasilkan regresi tumor pada banyak pasien [ 5 ]. Kemajuan ini telah menghasilkan pasien kanker dengan titik akhir survival yang lebih baik dan survival jangka panjang (LTS) yang lebih banyak (meskipun responden lengkap, CR, masih memiliki hasil yang lebih buruk daripada populasi umum). Dalam studi imuno-onkologi sebelumnya untuk terapi melanoma, seperti yang mengevaluasi ipilimumab dan nivolumab, hasilnya menunjukkan bahwa kurva survival ‘dataran tinggi’ untuk sebagian besar pasien LTS dalam periode waktu yang dicakup oleh kurva survival [ 6 , 7 ]. Artinya, kurva kelangsungan hidup yang mendasarinya menyatu ke probabilitas (secara substansial) lebih besar dari nol dan tampaknya tidak menurun lebih jauh. Perhatikan bahwa dalam praktiknya, di bagian ekor plateau Kaplan–Meier mungkin juga disebabkan oleh masalah pengambilan sampel, seperti ukuran sampel yang kecil atau data yang hilang, sehingga akan ada ketidakpastian tentang proporsi LTS yang sebenarnya. Ketika kurva kelangsungan hidup menunjukkan perilaku plateau ini, pendekatan model penyembuhan campuran (MCM) biasanya digunakan untuk menggambarkan pembuatan data yang mendasarinya. MCM menganggap populasi sebagai campuran dari dua kelompok: yang disembuhkan dan yang tidak disembuhkan. Dalam kasus kami, kelompok yang disembuhkan berisi pasien LTS. Dalam banyak analisis MCM, kelangsungan hidup yang terkait dengan fraksi populasi yang tidak disembuhkan diwakili oleh model bahaya proporsional Cox. Di samping pertimbangan ini, penting juga untuk memperhitungkan risiko tambahan yang dialami oleh pasien yang tidak disembuhkan karena kanker, di luar risiko mortalitas latar belakang populasi umum (yang disembuhkan). Model bahaya berlebih menyediakan kerangka kerja untuk memisahkan mortalitas dasar (bahaya latar belakang) dari risiko tambahan yang terkait dengan penyakit tersebut. Hal ini terutama penting ketika berhadapan dengan data kelangsungan hidup di mana pasien mungkin tidak semuanya memiliki risiko kematian yang sama.
Namun, plateau survival yang menunjukkan proporsi LTS mungkin belum tercapai pada saat pemotongan data (termasuk akhir studi yang direncanakan). Untuk mendapatkan kurva survival lengkap untuk digunakan dalam evaluasi HTA, kita perlu mengekstrapolasi kurva survival ke plateau yang berkelanjutan. Idealnya, ekstrapolasi ini harus konsisten antara pemotongan data [ 8 ]. Pertanyaan tentang bagaimana melakukan ini secara prinsip dan bermanfaat dalam situasi di mana uji coba mencakup beberapa lengan pengobatan dan titik akhir adalah subjek makalah ini. Fakta bahwa kita mempertimbangkan beberapa titik akhir dalam uji coba dalam analisis yang sama berarti bahwa informasi tentang plateau dari data untuk satu titik akhir berpotensi membantu menginformasikan estimasi plateau untuk titik akhir lainnya. Ini dapat memungkinkan konsistensi antara estimasi plateau dan memaksimalkan utilitas semua data yang tersedia.
Dalam paradigma frekuentis, contoh karya terkait adalah pendekatan pemodelan multilevel dalam pemodelan penyembuhan campuran menggunakan efek acak untuk memodelkan struktur pengelompokan multilevel dalam prediktor linier baik dalam fungsi bahaya maupun bagian probabilitas penyembuhan [ 9 ]. Korelasi antara efek acak dalam kelangsungan hidup yang tidak disembuhkan dan fraksi penyembuhan telah diselidiki menggunakan distribusi Normal bivariat [ 10 , 11 ]. Sebaliknya, kami akan memaksakan ketergantungan dengan hiperparameter. Sejauh pengetahuan kami, belum ada model penyembuhan campuran parametrik penuh Bayesian dengan struktur pemodelan multilevel untuk titik akhir.
Makalah ini disusun sebagai berikut. Di bagian berikutnya, contoh motivasi dan data yang digunakan di seluruh bagian diuraikan. Kami memperkenalkan model campuran dasar di Bagian 3.1 , sebelum memperluasnya ke model hierarki Bayesian kami di Bagian 3.2 . Di Bagian 5 , pendekatan pemodelan baru kami diterapkan pada kumpulan data contoh motivasi. Perbandingan dilakukan antara pendekatan kami dan model analog independen. Terakhir, di Bagian 6 kami membahas hasil dan pekerjaan di masa mendatang.
2 Contoh Motivasi
Contoh motivasi kami menyangkut studi jangka panjang terapi melanoma. Studi ini telah dijelaskan secara rinci di tempat lain, jadi kami memberikan tinjauan singkat data di sini (lihat [ 6 , 7 , 12 ] untuk rincian lebih lanjut). Uji coba CheckMate 067 adalah studi fase 3 acak, tersamar ganda yang dilakukan pada pasien yang memenuhi syarat berusia 18 tahun atau lebih dengan melanoma stadium III atau IV yang sebelumnya tidak diobati dan tidak dapat direseksi. Nivolumab sendiri atau kombinasi nivolumab plus ipilimumab dibandingkan dengan ipilimumab sendiri pada pasien dengan melanoma metastasis. Mereka ditugaskan secara acak dalam rasio 1:1:1 dan dikelompokkan berdasarkan status ekspresi anti–programmed death-1 ligand 1 (PD-L1), apakah ada mutasi pada gen BRAF yang membuatnya bekerja secara tidak benar (mutasi BRAF), dan stadium metastasis AJCC. Total sampel dasar terdiri dari
Subjek dibagi ke dalam tiga lengan pengobatan (i) monoterapi ipilimumab dengan 3 mg/kg IV sekali setiap 3 minggu (Q3W) untuk total 4 dosis; (ii) monoterapi nivolumab dengan 3 mg/kg intravena (IV) sekali setiap 2 minggu (Q2W); (iii) menggabungkan nivolumab dengan ipilimumab dengan 1 mg/kg IV dan 3 mg/kg IV Q3W, masing-masing, untuk 4 dosis diikuti oleh nivolumab 3 mg/kg IV Q2W. Titik akhir ko-primer adalah kelangsungan hidup bebas perkembangan (PFS; yaitu, waktu dari pengacakan hingga pertama perkembangan penyakit atau kematian) dan kelangsungan hidup keseluruhan (OS; yaitu, waktu dari pengacakan hingga saat kematian). Perkembangan penyakit didefinisikan sebagai respons tumor yang dievaluasi menggunakan kriteria dari RECIST (Response Evaluation Criteria in Solid Tumors), versi 1.1. Ini termasuk peningkatan ukuran yang signifikan, lesi baru atau memburuknya lesi yang ada. Sumber data untuk analisis terdiri dari data tingkat pasien mengenai waktu PFS dan OS dengan kovariat jenis kelamin, usia pada awal uji coba, dan negara pusat.
Dalam set data kami, tindak lanjut studi minimum dari pengacakan selama 60 bulan digunakan sebagai waktu pemotongan data akhir. Kami juga mempertimbangkan dua pemotongan data buatan sebelumnya dengan memotong data 60 bulan pada 12 dan 30 bulan. Waktu-waktu khusus ini dipilih untuk analisis ini karena studi aktual memiliki pemotongan data yang direncanakan pada 28 bulan, dan waktu median terbesar yang diamati untuk OS hanya lebih dari 30 bulan. Dengan demikian, waktu ini masuk akal dan relevan dengan uji coba, dan pada waktu ini mungkin untuk membuat kesimpulan yang sebanding dengan set data 60 bulan yang lengkap tetapi pada waktu yang jauh lebih awal. Selain itu, waktu median terbaru antara semua rejimen pengobatan untuk PFS adalah sekitar 12 bulan. Oleh karena itu, pada 12 bulan mungkin untuk mengkarakterisasi kurva kelangsungan hidup PFS tetapi bukan OS yang kurang matang sehingga meminjam informasi antara PFS dan OS mungkin menguntungkan. Mengambil pemotongan data pada waktu yang lebih awal mungkin tidak akan memberikan informasi yang cukup untuk memungkinkan ekstrapolasi yang berguna. Pasien yang masih dalam tahap tindak lanjut tetapi belum mengalami kejadian yang diinginkan pada saat pemotongan data buatan disensor pada saat ini.
Pembaca dianjurkan untuk merujuk pada analisis yang diterbitkan sebelumnya untuk hasil uji coba CheckMate 067, termasuk publikasi penguncian basis data (DBL) 5 tahun [ 7 ]. Singkatnya, untuk PFS, median (95% CI) waktu kejadian untuk setiap kelompok pengobatan adalah 2,86 bulan (2,79–3,29) untuk ipilimumab, 6,93 bulan (5,32–10,41) untuk nivolumab, dan 11,50 bulan (9,26–20,80) untuk pengobatan kombinasi nivolumab dan ipilimumab. Untuk OS, median (95% CI) waktu kejadian untuk setiap kelompok pengobatan adalah 20,0 bulan (17,22–25,6) untuk ipilimumab, 36,9 bulan (31,24–60,9) untuk nivolumab, dan tidak diamati untuk pengobatan kombinasi. Gambar 1 menunjukkan estimasi Kaplan–Meier dari kurva survival PFS dan OS untuk data lengkap dari uji coba fase 3 CheckMate 067. Kedua set kurva, untuk PFS dan OS, tampaknya mendekati probabilitas pembatas positif; kurva PFS lebih jelas demikian. Hasil awal yang dipublikasikan untuk hasil pada tindak lanjut 7,5 tahun terus menunjukkan ketahanan respons dengan nivolumab dan ipilimumab yang dikombinasikan, dan plateau survival yang sedang berlangsung [ 13 ].
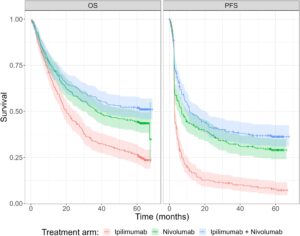
Analisis frekuentis standar telah dilakukan pada data ini dengan model penyembuhan campuran terpisah untuk setiap pengobatan dan OS atau PFS [ 14 ]. Diperkirakan bahwa untuk OS, rentang proporsi LTS yang diperkirakan adalah 16%–26% untuk ipilimumab, 38%–46% untuk nivolumab, dan 49%–54% untuk pengobatan gabungan di seluruh distribusi yang dimodelkan. Demikian pula, untuk PFS, rentang proporsi LTS adalah 9%–13% untuk ipilimumab, 29%–33% untuk nivolumab, dan 38%–40% untuk pengobatan gabungan.
3 Kerangka Pemodelan



3.1.1 Masalah Pemodelan Beberapa Titik Akhir
Ada beberapa masalah potensial dengan pendekatan yang ada untuk menyembuhkan pemodelan, ketika diterapkan pada konteks HTA, khususnya.
Pertama, ketika titik akhir berkorelasi, seperti dengan peristiwa umum yang menarik yaitu kelangsungan hidup secara keseluruhan (OS) dan kelangsungan hidup bebas perkembangan (PFS), hal ini harus diperhitungkan dalam pemodelan. Mungkin ada informasi dalam satu contoh waktu peristiwa yang dapat kita gunakan untuk meningkatkan inferensi dari yang lain. Melakukan analisis yang terpisah dan independen bahkan dapat memberikan hasil yang berlawanan dengan intuisi. Dalam kasus beberapa jenis titik akhir dalam uji coba yang sama, karena interpretasi klinis dari fraksi penyembuhan adalah proporsi pasien yang LTS, mungkin masuk akal secara intuitif bahwa ada satu fraksi penyembuhan yang mendasarinya. Misalnya, apa yang akan menjadi interpretasi jika ada perbedaan dalam plateaus kelangsungan hidup darurat antara PFS dan OS? Ini adalah dikotomi yang secara klinis tidak intuitif antara proporsi yang dihasilkan dari penyintas jangka panjang.
Kedua, data time-to-event biasanya disensor ke kanan karena penyensoran administratif atau kehilangan tindak lanjut. Waktu penyensoran mungkin terlalu dini untuk mengkarakterisasi model survival HTA secara memadai untuk satu titik akhir. Secara khusus, waktu OS dibatasi di bawah oleh waktu PFS menurut definisi, sehingga akan mengalami lebih banyak penyensoran pada titik potong yang sama. Dengan memanfaatkan kumpulan titik akhir secara bersamaan, kelangkaan data dapat dikurangi untuk memberikan kecocokan dan ekstrapolasi yang lebih baik ke seluruh rentang hidup pasien. Hal ini khususnya penting untuk pemodelan ekonomi kesehatan guna mengukur biaya dan dampak penuh dari suatu intervensi.
Lebih jauh lagi, jika ada penyensoran berat untuk semua titik akhir, seperti pemotongan data awal, dan jumlah titik akhir kecil, maka data itu sendiri mungkin tidak mewakili kurva kelangsungan hidup yang sebenarnya, termasuk dataran tinggi untuk fraksi penyembuhan. Pada titik ini, sumber informasi tambahan harus terutama dimasukkan ke dalam model. Paradigma Bayesian secara alami memungkinkan penyertaan bukti eksternal dari sumber-sumber seperti data historis dan pendapat ahli. Adalah masuk akal untuk berasumsi, jika tidak ada informasi tambahan, bahwa fraksi penyembuhan untuk semua titik akhir diambil dari distribusi yang sama atau sangat mirip. Untuk melakukan ini, kita dapat meningkatkan jumlah kekuatan untuk meminjam antara data titik akhir yang mencapai keseimbangan antara informasi (atau kekurangan) dalam data dan pengetahuan lainnya [ 16 ]. Secara praktis, ini sesuai dengan pengurangan hiperparameter varians fraksi penyembuhan global yang pada batasnya adalah model dasar dengan
, setara dengan pengumpulan data yang lengkap.
Kami sekarang akan menyajikan model penyembuhan campuran hierarkis Bayesian untuk beberapa titik akhir. Model ini memiliki keuntungan ganda, yaitu meminjam informasi antara titik akhir (misalnya, dalam kasus OS dan PFS, data PFS yang mungkin lebih matang dapat menginformasikan analisis OS yang seringkali sangat disensor) dan memperoleh estimasi fraksi penyembuhan tunggal.
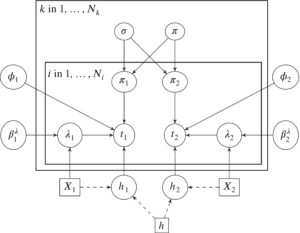
3.2 Model Penyembuhan Campuran Hirarkis


4 Studi Simulasi
Untuk menilai kinerja metode kami dalam mengatasi masalah yang ditetapkan di atas, kami melakukan studi simulasi dan membandingkan hasilnya antara skenario yang ditentukan [ 17 ]. Kami mengikuti pendekatan terstruktur untuk merancang dan melaporkan studi simulasi, yang dijelaskan dalam [ 18 ], yang melibatkan penentuan tujuan, mekanisme pembangkitan data, estimasi, metode, dan ukuran kinerja (‘ADEMP’).
4.1 Skenario dan Proses Pembuatan Data
Kami mensimulasikan waktu bertahan hidup dari berbagai model penyembuhan campuran hierarkis. Kami memutuskan untuk melakukan ini daripada mengambil sampel ulang dari kumpulan data yang ada karena fleksibilitas dan skenario yang diperluas yang disediakannya. Misalnya, contoh data nyata di Bagian 5 akan dibatasi hanya pada dua titik akhir.
Estimasi target yang digunakan adalah waktu bertahan hidup rata-rata terbatas (RMST) dan fraksi penyembuhan (
). Waktu bertahan hidup rata-rata (
) tidak digunakan. Hal ini dipilih karena sangat relevan untuk evaluasi ekonomi kesehatan. Pendekatan alternatif adalah menggunakan, misalnya, Concordance Index (C-index) atau uji log-rank yang lebih disukai dalam bidang analisis survival. Kami akan menggunakan versi RMST tertentu yang sesuai untuk model penyembuhan campuran 1 . Mendefinisikan
sebagai waktu maksimum (batasan) maka



4.2 Hasil Simulasi
Analisis utama menghasilkan 1000 sampel posterior untuk setiap set data skenario, yang direplikasi 1000 kali mengikuti Persamaan ( 4 ). Waktu proses melebihi beberapa jam menggunakan kluster berkinerja tinggi Myriad. Gambar dan tabel hasil tambahan yang ditemukan dalam Lampiran mencakup histogram distribusi posterior ukuran kinerja (Gambar A18 dan A19 ), plot lolipop yang membandingkan hasil terpisah dan hierarkis (Gambar A20–A25 ), dan plot zip cakupan (Gambar A26–A34 ). Untuk ringkasan keseluruhan, Tabel 1 menunjukkan estimasi ukuran kinerja yang dirata-ratakan pada semua kurva dalam skenario. Gambar A22 dan A23 dalam Lampiran memberikan peta panas yang sesuai untuk pengenalan pola yang mudah.
| RMST | Fraksi Penyembuhan | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bias | Cakupan | pekerja | RB | Bias | Cakupan | pekerja | RB | |||||||||
| Skenario | Disini | September | Disini | September | Disini | September | Disini | September | Disini | September | Disini | September | Disini | September | Disini | September |
| 1 | 0,01 | 0,01 | 0,99 | 0.86 | 0,03 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0,99 | 0.84 | 0,01 | 0.00 | 0,01 | 0.00 |
| 2 | 0,01 | 0,01 | 0,98 | 0,85 | 0,03 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0,98 | 0.83 | 0,01 | 0.00 | 0,01 | 0.00 |
| 3 | 0,01 | 0,01 | 0,96 | 0.84 | 0,03 | 0,01 | 0.00 | 0.00 | 0.00 | 0.00 | 0,96 | 0.84 | 0,01 | 0.00 | 0.00 | 0.00 |
| 4 | 0,01 | 0,01 | 0,94 | 0,85 | 0,03 | 0,01 | 0.00 | 0.00 | 0.00 | 0.00 | 0,93 | 0.84 | 0,01 | 0.00 | 0.00 | 0.00 |
| 5 | 0.57 | 0,50 | 0.21 | 0.10 | 0.22 | 0.16 | 0.18 | 0.16 | 0,04 | 0.00 | 0,95 | 0.83 | 0,08 | 0.00 | 0,15 | 0,01 |
| 6 | 0,55 | 0.42 | 0.34 | 0.14 | 0.28 | 0.21 | 0.19 | 0.14 | 0,06 | 0.00 | 0,94 | 0.83 | 0,09 | 0.00 | 0.22 | 0,01 |
| 7 | 0.57 | 0.39 | 0.12 | 0,02 | 0.14 | 0,09 | 0.19 | 0.14 | 0.12 | 0,01 | 0.35 | 0.72 | 0,05 | 0,01 | 0.46 | 0,05 |
| 8 | 0.52 | 0.37 | 0.18 | 0,04 | 0,15 | 0.10 | 0.18 | 0.14 | 0.10 | 0,01 | 0.48 | 0,75 | 0,05 | 0.00 | 0.36 | 0,04 |
| 9 | 0,01 | 0,01 | 1.00 | 0,97 | 0,06 | 0,01 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0,97 | 0,02 | 0.00 | 0,01 | 0.00 |
| 10 | 0,01 | 0,01 | 0,99 | 0,97 | 0,06 | 0,01 | 0,01 | 0.00 | 0.00 | 0.00 | 0,99 | 0,97 | 0,02 | 0.00 | 0,01 | 0,01 |
| 11 | 0,01 | 0,01 | 0,98 | 0,97 | 0,04 | 0,02 | 0.00 | 0.00 | 0.00 | 0.00 | 0,98 | 0,97 | 0,02 | 0,01 | 0.00 | 0.00 |
| 12 | 0,01 | 0,01 | 0,97 | 0,97 | 0,04 | 0,03 | 0.00 | 0.00 | 0.00 | 0.00 | 0,97 | 0,97 | 0,01 | 0,01 | 0.00 | 0.00 |
| 13 | 0.61 | 0.51 | 0.22 | 0.13 | 0.23 | 0.16 | 0.20 | 0.16 | 0,06 | 0.00 | 0,96 | 0,97 | 0,09 | 0.00 | 0.21 | 0,02 |
| 14 | 0.57 | 0.43 | 0.37 | 0.20 | 0.27 | 0.22 | 0.20 | 0.14 | 0,07 | 0.00 | 0,94 | 0,97 | 0,09 | 0.00 | 0.27 | 0,02 |
| 15 | 0.57 | 0.42 | 0.12 | 0,04 | 0.14 | 0,09 | 0.19 | 0.14 | 0.12 | 0,03 | 0.35 | 0,65 | 0,05 | 0,01 | 0.47 | 0.11 |
| 16 | 0.51 | 0.39 | 0.18 | 0,06 | 0,15 | 0.10 | 0.18 | 0,15 | 0.10 | 0,02 | 0.48 | 0.73 | 0,05 | 0,01 | 0.36 | 0,09 |
| 17 | 0.20 | 0.36 | 0,93 | 0.92 | 0.19 | 0.20 | 0,08 | 0.13 | 0,07 | 0.13 | 0,94 | 0,93 | 0,07 | 0,07 | 0.26 | 0,50 |
| 18 | 0,08 | 0.38 | 0,95 | 0,91 | 0,15 | 0.23 | 0,03 | 0.16 | 0,02 | 0.13 | 0,95 | 0.92 | 0,05 | 0,07 | 0,09 | 0.48 |
| 19 | 0,03 | 0,08 | 0,95 | 0,94 | 0.10 | 0.14 | 0,01 | 0,03 | 0,01 | 0,03 | 0,95 | 0,94 | 0,04 | 0,05 | 0,03 | 0.10 |
| 20 | 0,01 | 0,08 | 0,94 | 0,94 | 0,06 | 0,15 | 0,01 | 0,03 | 0.00 | 0,03 | 0,94 | 0,95 | 0,02 | 0,05 | 0,01 | 0.10 |
| 21 | 0,91 | 0,90 | 0,09 | 0.18 | 0.19 | 0.21 | 0.32 | 0.31 | 0.20 | 0.21 | 0.34 | 0.54 | 0,08 | 0,08 | 0,75 | 0,78 |
| 22 | 0.84 | 0,87 | 0.10 | 0.26 | 0.21 | 0.24 | 0.32 | 0.33 | 0.17 | 0.20 | 0.17 | 0,60 | 0,05 | 0,09 | 0,65 | 0.74 |
| 23 | 0.63 | 0.62 | 0,06 | 0,08 | 0,15 | 0.14 | 0.22 | 0.21 | 0.14 | 0,15 | 0.23 | 0.30 | 0,05 | 0,05 | 0.53 | 0.56 |
| 24 | 0.56 | 0.57 | 0.11 | 0.13 | 0,15 | 0,15 | 0.21 | 0.21 | 0.11 | 0.12 | 0.44 | 0.45 | 0,05 | 0,05 | 0.41 | 0.45 |
| 25 | 0.19 | 0.36 | 0,95 | 0,91 | 0.20 | 0.21 | 0,07 | 0.13 | 0,07 | 0.13 | 0,95 | 0.92 | 0,07 | 0,07 | 0,25 | 0,50 |
| 26 | 0,08 | 0.38 | 0,97 | 0,91 | 0,15 | 0.23 | 0,03 | 0,15 | 0,02 | 0.13 | 0,97 | 0.92 | 0,05 | 0,07 | 0,09 | 0.48 |
| 27 | 0,03 | 0,08 | 0,97 | 0,95 | 0.10 | 0.14 | 0,01 | 0,03 | 0,01 | 0,03 | 0,97 | 0,95 | 0,04 | 0,05 | 0,03 | 0.10 |
| 28 | 0,01 | 0,08 | 0,96 | 0,94 | 0,06 | 0,15 | 0.00 | 0,03 | 0.00 | 0,03 | 0,96 | 0,95 | 0,02 | 0,05 | 0,01 | 0.10 |
| 29 | 0,91 | 0,91 | 0.11 | 0.16 | 0.20 | 0.20 | 0.32 | 0.32 | 0.20 | 0.21 | 0.39 | 0.54 | 0,08 | 0,09 | 0.74 | 0,78 |
| 30 | 0.84 | 0,87 | 0.13 | 0.26 | 0.22 | 0,25 | 0.32 | 0.33 | 0.17 | 0.20 | 0,25 | 0,60 | 0,06 | 0,09 | 0,65 | 0.73 |
| 31 | 0.63 | 0.62 | 0,07 | 0,09 | 0.14 | 0.14 | 0.22 | 0.21 | 0.14 | 0,15 | 0,25 | 0.31 | 0,05 | 0,05 | 0.54 | 0.56 |
| 32 | 0.56 | 0.57 | 0.11 | 0.13 | 0,15 | 0,15 | 0.20 | 0.21 | 0.11 | 0.12 | 0.44 | 0.45 | 0,05 | 0,05 | 0.41 | 0.45 |
4.2.1 Kinerja Estimasi Target
Baik untuk RMST maupun fraksi penyembuhan, gambarannya serupa. Jika kurva kelangsungan hidup yang belum disembuhkan dan distribusi prior fraksi penyembuhan bersifat informatif, maka model terpisah dan hierarkis berkinerja baik dengan ukuran bias yang relatif kecil, terlepas dari apakah prior informatif atau lemah ditempatkan pada varians antar kelompok. Namun, dalam skenario ini cakupannya lebih baik untuk model terpisah. Sebaliknya, ketika kelangsungan hidup yang belum disembuhkan dan fraksi penyembuhan hanya memiliki prior informatif yang lemah, maka model terpisah dan hierarkis menunjukkan bias yang buruk, terlepas dari prior antar kelompok (skenario 1–4, 9–12). Skenario yang perlu diperhatikan adalah ketika kita memiliki prior informatif untuk parameter kurva kelangsungan hidup yang belum disembuhkan tetapi hanya pengetahuan prior yang lemah untuk fraksi penyembuhan (skenario 17–20, 25–28). Dalam kasus ini, bias model hierarkis jelas lebih baik daripada untuk model terpisah. Cakupannya secara konsisten lebih baik untuk skenario dengan prior kurva kelangsungan hidup yang informatif juga. Dalam hal ukuran sampel, perbedaan terbesar antara sampel kecil dan besar adalah ketika fraksi penyembuhan memiliki prior yang lemah; atau sebagai alternatif, dengan bukti prior yang kuat maka pengukurannya kurang sensitif terhadap ukuran sampel. Untuk cakupan, ketika biasnya relatif besar maka cakupannya rendah dan sebaliknya. Secara khusus, untuk sejumlah kecil titik akhir dan ukuran sampel yang kecil, model hierarkis berkinerja lebih baik dalam hal bias ketika kurva survival informatif prior digunakan dengan prior fraksi penyembuhan yang lemah (skenario 18 dan 26). Sebaliknya, untuk prior yang lemah untuk survival yang tidak disembuhkan dan fraksi penyembuhan yang informatif (skenario 5–8, 13–16) cakupan dan bias lebih buruk untuk model hierarkis daripada model terpisah, tetapi secara umum ketika prior survival yang tidak disembuhkan lemah maka cakupannya buruk.
Singkatnya, pola ukuran kinerja antara estimasi target serupa. Ini mungkin karena RMST bergantung pada fraksi penyembuhan dari kurva yang mendasarinya. Secara keseluruhan, studi simulasi menunjukkan bahwa kinerja estimasi dapat bervariasi tergantung pada fraksi penyembuhan, kurva kelangsungan hidup yang tidak disembuhkan, dan ukuran sampel. Skenario ketika ada lebih sedikit pengetahuan sebelumnya tentang kurva kelangsungan hidup yang tidak disembuhkan dan lebih banyak informasi tentang fraksi penyembuhan tampaknya lebih menyukai model terpisah, sedangkan sebaliknya skenario di mana model hierarkis paling bermanfaat mencakup yang memiliki informasi sebelumnya tentang kelangsungan hidup yang tidak disembuhkan dan ketidakpastian tentang fraksi penyembuhan. Kasus terakhir ini tampaknya masuk akal dalam kenyataan ketika, misalnya, obat baru memengaruhi proporsi yang tidak pasti dari para penyintas jangka panjang untuk proses yang mendasarinya yang dipahami dengan baik. Sebaliknya, dalam situasi lain, mungkin tidak mungkin untuk mendapatkan bukti langsung tentang populasi yang tidak diobati karena pertimbangan etika.
5 Contoh Data Nyata
Pada bagian ini, kami menerapkan model dari Bagian 3.2 ke kumpulan data CheckMate 067. Pertama-tama, kami merinci aspek pemodelan yang khusus untuk analisis ini sebelum menyajikan hasilnya.
Analisis ini dilakukan menggunakan mesin inferensi Stan [ 19 ] yang dipanggil dari R v.4.3.1 [ 20 ] menggunakan paket rstan pada PC Windows 11 dengan 12 inti. Setiap kecocokan menggunakan default 4 rantai masing-masing 2000 iterasi, dan pemanasan 100 iterasi. Untuk menentukan konvergensi, kami memeriksa ukuran sampel efektif, kesalahan standar rantai Markov, dan melakukan pemeriksaan prediktif posterior. Rincian pemeriksaan model dapat ditemukan di Bagian Lampiran 8. Kode telah dikembangkan menjadi paket R menggunakan kerangka kerja yang dapat digeneralisasikan. Ini berarti bahwa analisis untuk sejumlah titik akhir yang sewenang-wenang dapat dengan mudah dilakukan dengan data baru. Paket ini tersedia secara bebas dan dapat diunduh dari https://github.com/StatisticsHealthEconomics/multimcm .
5.1 Latar Belakang Kelangsungan Hidup

Kami menggunakan tabel kehidupan Organisasi Kesehatan Dunia (WHO) menurut negara untuk tahun terbaru yang tersedia yaitu 2016 [ 21 ] untuk menginformasikan mortalitas latar belakang dalam model pengobatan campuran. Bahaya dasar adalah tingkat mortalitas yang diharapkan untuk setiap pasien pada usia saat mereka mengalami kejadian tersebut. Data mortalitas disesuaikan dengan negara, usia, dan jenis kelamin. Dengan demikian, struktur ini memberikan gambaran terperinci tentang profil pasien yang berbeda dalam uji klinis. WHO melaporkan probabilitas kematian bersyarat dalam interval 5 tahun hingga usia 85 tahun. Tingkat mortalitas tahunan yang konstan dilaporkan untuk individu yang berusia di atas 85 tahun. Tabel kehidupan dibuat dengan asumsi bahwa tidak ada seorang pun yang hidup lebih dari 100 tahun. Rincian lebih lanjut disediakan di Bagian Lampiran 2 .

Mungkin saja pasien dalam uji coba memiliki latar belakang kelangsungan hidup yang lebih buruk daripada rata-rata individu yang setara dalam populasi umum, sehingga dengan naif menggunakan tabel kehidupan WHO akan melebih-lebihkan waktu kelangsungan hidup mereka. Ada beberapa kemungkinan cara untuk mengatasi hal ini. Misalnya, dengan hanya menggunakan responden lengkap dalam sampel, yang secara klinis dikonfirmasi telah sembuh, adalah mungkin untuk memperoleh distribusi posterior untuk rasio bahaya antara mereka dan garis dasar estimasi WHO. Ini dapat berfungsi sebagai prior dalam model utama dalam pendekatan dua langkah. Atau, keyakinan sebelumnya dapat didefinisikan secara eksplisit menggunakan pengetahuan ahli. Ini dapat diperoleh secara langsung untuk rasio bahaya atau pada skala alami, seperti rata-rata masa hidup, dan ditransformasikan.
5.2 Kelangsungan Hidup yang Tidak Tersembuhkan
Distribusi yang tidak sembuh diasumsikan sama untuk setiap obat. Artinya, kami berasumsi bahwa jika seorang pasien tidak sembuh maka masuk akal untuk mempertimbangkan mereka dalam beberapa hal dalam keadaan yang setara dengan sebelum menerima pengobatan. Dalam konteks klinis tertentu dari contoh dunia nyata, asumsi bahwa semua obat memiliki distribusi yang tidak sembuh yang sama dianggap masuk akal secara klinis karena obat-obatan tersebut serupa dalam mekanisme aksi dan jalur biologisnya. Larkin (2019) [ 7 ] membahas kesamaan di antara inhibitor titik pemeriksaan imun karena mekanisme aksi imunologisnya yang sama.
5.3 Spesifikasi Sebelumnya


5.4 Model Parametrik untuk Variabilitas Sampling
Untuk memodelkan variabilitas pengambilan sampel dalam waktu kejadian OS dan PFS yang diamati, kami menggunakan distribusi eksponensial, Weibull, Gompertz, log-normal, dan log-logistik. Ini adalah beberapa di antara yang direkomendasikan oleh pedoman NICE untuk Penilaian Teknologi Kesehatan (HTA) [ 1 ]. Secara umum, penyediaan daftar ini telah ditafsirkan oleh banyak orang dalam literatur HTA yang berarti semua distribusi ini harus dimodelkan dengan set data tertentu. Pendekatan preskriptif ini tidak memperhitungkan apa yang mungkin diketahui apriori tentang masalah tersebut. Pada kenyataannya, sebagian kecil dari model parametrik ini akan lebih masuk akal untuk data tersebut sehingga inilah yang harus diselidiki.
5.5 Penilaian Model
Kami mengevaluasi kebaikan kecocokan dari keseluruhan model menggunakan prediksi di luar sampel yang diestimasi dengan kriteria informasi yang berlaku secara luas (WAIC) (dan validasi silang keluar-satu, LOO, diberikan di Bagian Lampiran 6 ) [ 25 ]. Ini memiliki berbagai keuntungan untuk AIC dan DIC yang lebih umum. WAIC adalah perbedaan antara kepadatan prediktif titik log yang dihitung dan jumlah parameter efektif yang diestimasi. Nilai yang lebih kecil lebih baik. Ini sepenuhnya Bayesian dan invarian terhadap parameterisasi. Mereka mudah diperoleh dengan menggunakan sampel posterior dari keluaran Stan.
Belum banyak pekerjaan yang dilakukan hingga saat ini pada metode penilaian model yang khusus untuk model penyembuhan campuran. Untuk model penyembuhan campuran dasar, penilaian dapat difokuskan pada model secara keseluruhan atau pada submodel insiden dan latensi secara terpisah. Kesesuaian submodel latensi dapat diperiksa menggunakan residual Schoenfeld yang direvisi [ 26 ], dan kinerja submodel insiden dapat diperiksa dengan ukuran konkordansi seperti AUC [ 27 ]. Namun, pendekatan model insiden ini paling baik digunakan secara langsung dengan status penyembuhan yang diketahui dan dirancang untuk model yang mempertimbangkan fraksi penyembuhan individual, tidak seperti model kami yang mengasumsikan fraksi penyembuhan populasi tunggal. Untuk perluasan model penyembuhan campuran dasar tersebut, masih menjadi pertanyaan terbuka tentang cara terbaik untuk menerapkan dan mengadaptasi metode ini dalam konteks ini untuk memastikan hasil yang kuat dan dapat ditafsirkan.
5.6 Hasil Berdasarkan Data Tindak Lanjut 60 Bulan Penuh
Pada bagian ini, kami akan mengeksplorasi kecocokan model penyembuhan campuran menggunakan data uji CheckMate 067 60 bulan yang lengkap. Contoh kurva kelangsungan hidup posterior model hierarki Bayesian menggunakan data lengkap dan distribusi eksponensial untuk OS dan PFS ditunjukkan pada Gambar 4. Kami menunjukkan ini karena, meskipun eksponensial adalah distribusi rekomendasi NICE yang paling sederhana, dari inspeksi visual, model ini cukup cocok. Plot ekuivalen untuk semua distribusi lain dan plot gabungan diberikan di Bagian Lampiran 5 .
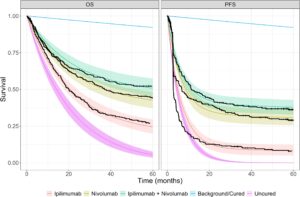
Kelangsungan hidup latar belakang tampak menurun pada tingkat yang kecil dan stabil serta sama di antara plot, seperti yang diharapkan karena estimasi titik dari tabel kehidupan WHO digunakan secara langsung. Inspeksi visual menunjukkan kecocokan model yang cukup baik. Kurva PFS Kaplan–Meier menunjukkan penurunan tajam awal sebelum mendatar. Eksponensial sangat cocok dengan ekor yang sangat penting karena di sinilah biasanya ekstrapolasi memiliki kecocokan terburuk.
Untuk waktu tindak lanjut 60 bulan dan untuk model eksponensial, RMST (interval kredibel 95%, CrI) untuk kelompok yang belum sembuh adalah 20,6 (18,4, 23,1) dan 6,66 (6,09, 7,39) bulan, untuk OS dan PFS, masing-masing. Untuk titik akhir OS, RMST adalah 28,7 (26,3, 31,1), 36,5 (34,1, 38,9) dan 39,6 (37,1, 42,1) bulan, untuk ipilimumab, nivolumab dan gabungan, masing-masing. Untuk titik akhir PFS, RMST adalah 11,9 (10,0, 14,1), 24,3 (21,1, 27,4) dan 27,7 (24,7, 30,8) bulan, untuk ipilimumab, nivolumab dan gabungan, masing-masing. RMST untuk populasi yang sembuh adalah nilai yang sama yang sesuai dengan populasi umum yaitu 58,2 bulan.
Fraksi penyembuhan global posterior relatif lebar, yang dapat dimengerti karena hanya ada dua titik yang dapat dipertukarkan yang memberikan informasi terbatas (OS dan PFS). Kisarannya 0,1–0,55, 0,2–0,6, 0,2–0,65 untuk ipilimumab, nivolumab, dan pengobatan gabungan. Namun, meskipun demikian, data memengaruhi fraksi penyembuhan titik akhir dengan menarik lokasi pusat menjauh dari sebelumnya, ke bawah untuk ipilimumab dan ke atas untuk pengobatan gabungan. Untuk ipilimumab, fraksi kurva PFS posterior mendekati nol dalam interval kredibel. Sedangkan untuk nivolumab dan lengan pengobatan gabungan, fraksi penyembuhan global rata-rata terletak di suatu tempat antara rata-rata PFS dan OS, rata-rata global ipilimumab lebih dekat ke rata-rata fraksi penyembuhan OS. Ini karena kami telah secara eksplisit mengkodifikasikan dalam distribusi sebelumnya bahwa fraksi penyembuhan global tidak mungkin mendekati nol dan fraksi penyembuhan PFS posterior mendekati nol. Kami akan mengamati perilaku yang setara jika distribusi OS mendekati 1. Kurva survival untuk seluruh sampel mencapai plateau hingga survival mortalitas latar belakang saat probabilitas survival yang tidak disembuhkan mencapai nol. Karena latar belakang disediakan oleh pengguna, dalam hal ini dari tabel kehidupan WHO, maka tidak ada wawasan tambahan sejak saat ini dan seterusnya. Waktu terjadinya hal ini relatif awal untuk PFS dan distribusi log-Normal. Membandingkan model hierarkis dan terpisah, tidak ada perbedaan yang nyata antara keduanya. Seperti disebutkan di atas, informasi terbatas dengan hanya dua titik akhir dan prior yang cukup lemah. Model hierarkis Bayesian memungkinkan adaptasi otomatis antara pengumpulan penuh dan tanpa pengumpulan tergantung pada kekuatan bukti dalam data [ 28 ]. Ada sedikit penyusutan sehingga distribusi posterior untuk OS dan PFS ditarik ke arah mean global, sehingga fraksi penyembuhan PFS lebih besar dan fraksi penyembuhan OS lebih kecil dalam model hierarkis daripada model terpisah.
5.7 Hasil dari Pemotongan Data Interim dan Final
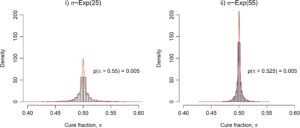
Sekarang kita mengalihkan perhatian kita untuk menyesuaikan model penyembuhan campuran dengan potongan data sebelumnya dalam set data uji coba CheckMate 067. Untuk set data lengkap hingga 60 bulan, kita telah melihat bahwa model terpisah dan hierarkis menghasilkan inferensi parameter yang serupa. Hal ini diharapkan ketika data relatif matang, pada dasarnya hanya ada dua titik data pada tingkat fraksi penyembuhan global dan prior lemah digunakan untuk hiperparameter varians global. Untuk tujuan demonstrasi, kami menunjukkan hasil menggunakan prior kompleksitas yang dihukum dengan parameter laju distribusi eksponensial
untuk skenario pemotongan data 12 bulan dan mempertahankan semua prior sebelumnya, termasuk prior lemah untuk mean
Ingatlah bahwa untuk waktu-waktu berikutnya, ketika lebih banyak data tersedia, varians alternatif sebelumnya diadopsi.
Gambar 5a,b menunjukkan plot hutan estimasi fraksi penyembuhan selama 12, 30 dan 60 bulan, dan untuk model terpisah dan hierarkis, masing-masing. Hasil ditunjukkan untuk model eksponensial OS dengan model eksponensial PFS dan OS log-Normal dengan model log-Normal PFS. Kita dapat melihat bahwa pada Gambar 5a untuk model eksponensial dalam kurva survival OS untuk model terpisah terdapat lebih banyak ketidakpastian daripada dalam plot ekuivalen untuk model hierarkis pada Gambar 5b . Kurva survival OS model log-Normal untuk model terpisah dan hierarkis melebih-lebihkan fraksi penyembuhan pada pemotongan data sebelumnya dan semua lengan perawatan. Untuk pemotongan data selanjutnya, fraksi penyembuhan tampak konvergen dari atas ke estimasi data lengkap.

Sebaliknya, untuk model terpisah dan semua kelompok perlakuan, pada tindak lanjut 12 bulan, model eksponensial meremehkan fraksi penyembuhan OS dan mendekati nilai data lengkap dari bawah. Ini kurang jelas dibandingkan dengan model log-Normal mungkin karena ketidakpastian estimasi yang lebih besar untuk model eksponensial. Yang terpenting, ini adalah dua perilaku yang jelas berbeda tetapi kita tidak akan tahu mana yang benar (jika ada) sampai nanti dalam uji coba. Untuk OS dalam model hierarkis, estimasi fraksi penyembuhan tampaknya akurat dan lebih pasti bahkan pada 12 bulan untuk semua kelompok perlakuan. Posterior lebih stabil tentang fraksi penyembuhan data lengkap untuk semua pemotongan data yang dipertimbangkan.
Gambar 6 menunjukkan kurva survival untuk pemotongan data dengan data tindak lanjut selama 12 bulan untuk model eksponensial dan terpisah serta hierarkis. Angka untuk pemotongan data selama 30 bulan dan tabel estimasi survival pada 60 bulan yang diekstrapolasi menggunakan titik pemotongan data selama 12 dan 30 bulan diberikan di Bagian Lampiran 5 dan 6 .
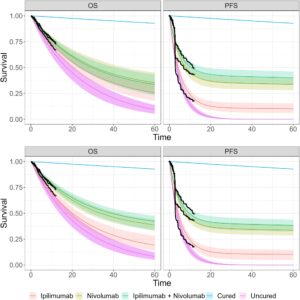
Dengan membandingkan RMST yang belum diawetkan untuk berbagai model, model eksponensial hierarkis memberikan waktu untuk OS 20,6 (18,4, 23,1) dan PFS 6,72 (6,15, 7,34) bulan. Untuk model terpisah, OS adalah 22,3 (18,5, 26,9) dan PFS adalah 5,68 (4,9, 6,45) bulan. Untuk model hierarkis log-Normal, RMST untuk titik akhir OS adalah 6,6 (6,17, 7,13) dan PFS adalah 3,98 (3,84, 4,12) bulan. Terakhir, model terpisah memberikan waktu 6,59 (6,18, 7,07) bulan untuk OS dan 3,98 (3,85, 4,1) bulan untuk PFS.
6 Diskusi
Kami telah menyajikan model penyembuhan campuran hierarki Bayesian untuk memperoleh kurva kelangsungan hidup lengkap yang menunjukkan perilaku plateau. Kurva ini kemudian dapat digunakan dalam HTA untuk menginformasikan fungsi-fungsi seumur hidup pasien. Kami juga melakukan studi simulasi yang menunjukkan situasi-situasi di mana model hierarki atau terpisah lebih tepat. Akhirnya, kami menunjukkan metode baru menggunakan set data uji coba CheckMate 067 untuk titik akhir OS dan PFS dan pada pemotongan data buatan yang berbeda; menggabungkan struktur tambahan untuk situasi khusus ini. Model hierarki dibandingkan dengan model analog terpisah dan telah terbukti lebih unggul, serta berprinsip dan berlaku untuk situasi-situasi di mana uji coba mencakup beberapa lengan pengobatan dan titik akhir.
Pendekatan kami mungkin lebih baik daripada model frekuentis atau nonhierarkis baik secara praktis, seperti yang ditunjukkan dalam studi simulasi, maupun secara konseptual, mengingat kerangka teoritis yang mendasarinya. Manfaat mengadopsi paradigma Bayesian daripada pendekatan frekuentis adalah fleksibilitas dalam memodelkan struktur kompleks, dalam kasus khusus kami data bertingkat atau bertingkat. Sebaliknya, model frekuentis perlu memaksakan asumsi tentang struktur matriks kovariansi. Keuntungan lain dari mengadopsi struktur hierarkis dalam pendekatan Bayesian adalah ketahanan terhadap ukuran sampel yang lebih kecil karena penyediaan informasi sebelumnya dan peminjaman kekuatan antara data untuk titik akhir yang berbeda, yang mengarah pada estimasi ekstrapolasi yang lebih stabil dan akurat. Spesifikasi distribusi sebelumnya yang berprinsip tentang fraksi penyembuhan terbukti sangat berguna di awal uji coba ketika data yang dapat diamati tentang penyintas jangka panjang lemah. Hal ini menghasilkan stabilisasi estimasi fraksi penyembuhan, yang sekali lagi menghasilkan ekstrapolasi yang lebih baik. Secara umum, ekstrapolasi hasil kelangsungan hidup dengan fraksi penyembuhan bersama memberikan pendekatan yang lebih konservatif dan praktis untuk memodelkan titik akhir secara terpisah. Mungkin saja terjadi peminjaman informasi yang berlebihan antara fraksi-fraksi penyembuhan ketika titik-titik akhir sangat berbeda. Dalam contoh kami, hal ini tidak diperlukan, karena hanya ada dua titik akhir, tetapi untuk jumlah yang lebih besar, hal ini mungkin sesuai. Pertukaran parsial dapat digunakan sebagai gantinya dalam kasus ini [ 29 ].
Dibandingkan dengan beberapa pendekatan frekuentis sebelumnya, kerangka kerja kami mampu menyertakan informasi kontekstual tentang parameter model melalui distribusi sebelumnya. Menggabungkan informasi yang masuk akal, baik dalam bentuk sumber data eksternal atau yang diperoleh dari para ahli dapat menstabilkan inferensi pada fraksi penyembuhan dan membatasi/membatasi nilainya melalui distribusi sebelumnya. Untuk analisis yang disajikan dalam makalah ini, kami memanfaatkan prior yang berbeda. Prior yang informatif minimal memungkinkan data mendominasi posterior, bahkan ketika kumpulan data relatif kecil. Dalam praktiknya, mungkin ada informasi tambahan dari pengalaman klinis atau data sebelumnya yang dapat menginformasikan pemilihan prior dengan lebih baik. Prior dapat ditentukan pada skala alami untuk membantu penggalian dan interpretasi. Misalnya, kita mungkin memiliki pengetahuan klinis bahwa perawatan obat dapat menghasilkan fraksi penyembuhan lebih besar dari, katakanlah, 30%. Jika seorang pasien (kanker) memasuki penelitian pada usia 60 tahun, maka ada tingkat kepastian yang tinggi bahwa mereka tidak akan hidup selama, katakanlah, lebih dari 40 tahun. Dalam kasus data yang jarang, misalnya, ketika terdapat sejumlah besar data yang hilang mungkin karena penyensoran yang tepat, maka ‘mengatur’ kesimpulan berdasarkan informasi sebelumnya yang tersedia dapat membuat perbedaan yang signifikan dan penting. Secara khusus, metode kurva pencampuran merupakan pilihan yang baru dan mudah untuk membatasi kelangsungan hidup [ 30 ]. Cara memperoleh informasi sebelumnya ini dalam praktik mungkin tidak sederhana dan protokol formal harus diadopsi [ 31 ].
Metode yang kami usulkan memodelkan struktur korelasi melalui fraksi penyembuhan. Namun, beberapa model efek acak alternatif juga dapat dipertimbangkan. Misalnya, yang lebih umum dalam pemodelan kelangsungan hidup relatif, kelemahan bersama dapat diperkenalkan pada skala bahaya berlebih, atau efek acak dapat diterapkan pada skala prediktor linier. Pendekatan ini sedikit berbeda, karena mereka memaksakan struktur korelasi langsung pada komponen laten model. Dalam kasus kami, fraksi penyembuhan adalah fokus utama minat klinis, dan menyusun model dengan cara ini memfasilitasi pengumpulan estimasi fraksi penyembuhan tunggal di seluruh kelompok. Formulasi ini juga bisa dibilang lebih intuitif bagi para profesional medis dan menawarkan beberapa efisiensi komputasi. Dalam pekerjaan di masa mendatang, akan sangat berharga untuk mengeksplorasi berbagai model efek acak di berbagai skenario untuk lebih memahami kinerja komparatifnya.
Regulator perawatan kesehatan, seperti Badan Obat-obatan Eropa (EMA) dan Badan Pengawas Obat dan Makanan AS (FDA), mungkin menghargai fakta bahwa model hierarkis dapat menanamkan beberapa bentuk pengetahuan sebelumnya untuk memperhitungkan skeptisisme. Ini akan mencegah tingkat penyembuhan diambil begitu saja, terutama dengan data yang terbatas. Model hierarkis tampaknya memberikan estimasi tingkat penyembuhan yang lebih tepat, bahkan dengan pemotongan data sebelumnya (terutama untuk model eksponensial). Model hierarkis lebih selaras, yang berarti kemungkinan estimasi yang lebih andal sejak awal, yang merupakan argumen yang bagus untuk melengkapi pemodelan berdasarkan pemotongan sebelumnya.
Dalam analisis kami, kami melakukan simulasi penyensoran akibat pemotongan data dengan hanya menyensor semua pasien dalam set data lengkap pada titik waktu yang sama. Dalam praktiknya, waktu penyensoran yang lebih realistis mungkin adalah tanggal kunjungan terakhir untuk setiap pasien; namun, hal ini tidak akan memengaruhi hasil analisis ini. Pertama-tama, titik pemotongan data dipilih untuk menunjukkan justifikasi teoritis metode kami dan bukan untuk secara ketat mengikuti protokol pemotongan data studi.

Utilitas penghentian harus menyertakan ukuran ketahanan ekstrapolasi kelangsungan hidup dan dapat mencakup manfaat, seperti biaya yang lebih rendah, waktu yang lebih leluasa dari uji klinis bagi pasien dan mereka yang menjalankan studi, waktu yang lebih cepat untuk memasarkan obat, dan menghindari efek samping. Utilitas juga akan bergantung pada estimasi nilai parameter yang ‘benar’ dari data yang tersedia, yaitu, bahwa nilai tersebut berada dalam ambang batas yang dapat diterima dari nilai sebenarnya. Ini dapat diterapkan secara langsung pada parameter yang diinginkan atau statistik urutan obat mana yang dianggap lebih baik.
Hal ini dapat dibingkai dalam hal nilai informasi (VoI) [ 34 ]. Misalnya, dalam kasus yang diberikan di atas, apa nilai tambahan dari memperoleh data lebih lanjut setelah 12 dan 30 bulan. Dalam praktiknya, memperoleh serangkaian heuristik mungkin lebih baik daripada memformalkan aturan umum. Serangkaian titik potong diskrit dapat digunakan, mirip dengan seleksi buatan kita dengan waktu pembulatan 12 dan 30 bulan, daripada mempertimbangkan seluruh garis nyata.
Selain selama penelitian, MCM hierarkis dapat digunakan sebelum penelitian untuk menginformasikan desain uji coba dan waktu tindak lanjut yang optimal untuk mendukung pilihan pemotongan data yang digunakan dalam praktik. Ukuran sampel yang lebih kecil dan durasi yang lebih pendek dapat memberikan daya yang setara mengingat pemanfaatan struktur model tambahan.
Ada beberapa implikasi untuk HTA dengan menggunakan model penyembuhan campuran hierarkis yang disajikan di sini. Dalam analisis efektivitas biaya, estimasi yang tidak stabil dari waktu ke waktu akan memberikan estimasi manfaat yang berbeda dan dengan demikian statistik efektivitas biaya dan kemungkinan keputusan optimal yang berbeda. Lee (2019) [ 35 ] melakukan analisis efektivitas biaya penggunaan nivolumab dengan ipilimumab vs. ipilimumab menggunakan data uji coba CheckMate 067, dan model kelangsungan hidup terpartisi dan model transisi status Markov. Biaya dan manfaat seumur hidup diestimasikan. Hasil diperoleh dengan menggunakan pemotongan data CheckMate 067 18 bulan (ketika data OS tidak tersedia) dan 36 bulan (OS tersedia). Mereka menunjukkan bahwa model yang menggunakan data OS menghasilkan lebih dari 1 tahun hidup tambahan yang disesuaikan dengan kualitas (QALY) di kedua lengan pengobatan dibandingkan dengan model tanpa data OS. Dengan menggunakan pendekatan kami, kami telah menunjukkan bahwa estimasi kurva kelangsungan hidup lengkap yang andal untuk OS dapat diperoleh bahkan untuk pemotongan data awal. Ini dapat digunakan untuk memperkirakan manfaat cakrawala seumur hidup dalam kasus-kasus di mana perkiraan tersebut sebelumnya tidak tersedia. Dalam contoh kami, fraksi penyembuhan OS akurat dan stabil pada 12 bulan untuk model penyembuhan campuran hierarkis dengan distribusi eksponensial untuk model kelangsungan hidup OS dan PFS yang tidak sembuh. Manfaat tambahan adalah potensi akhir uji coba yang lebih awal (lebih murah, kesehatan yang lebih baik, obat yang lebih cepat dipasarkan untuk keuntungan produsen dan pasien), dan uji coba yang lebih kecil.