ABSTRAK
Kami menyelidiki proses lazy burning untuk kotak Latin dengan mempelajari hipergraf terkaitnya. Dalam lazy burning, sekumpulan simpul dalam hipergraf awalnya dibakar, dan pembakaran tersebut menyebar ke simpul tetangga seiring waktu melalui aturan propagasi yang ditentukan. Angka lazy burning adalah jumlah minimum simpul yang awalnya dibakar yang akhirnya membakar semua simpul. Hipergraf yang terkait dengan kotak Latin meliputi:persamaan matematika-hipergraf seragam, yang titik sudut dan hipertepinya bersesuaian dengan entri dan garis (yaitu, kumpulan baris, kolom, atau simbol) dari kotak Latin, dan hipergraf seragam 3, yang memiliki titik sudut yang bersesuaian dengan garis kotak Latin dan hipertepi yang disebabkan oleh entri-entrinya. Dengan menggunakan urutan titik sudut yang bersama-sama membentuk penutup titik sudut, kami menunjukkan bahwa untuk kotak Latin dengan ordepersamaan matematika, angka pembakaran malas daripersamaan matematika-hipergraf seragam dibatasi di bawah olehpersamaan matematikadan di atas olehpersamaan matematikaBatasan ini ditunjukkan ketat menggunakan kuadrat Latin siklik dan pangkat interkalasi. Untuk kasus hipergraf 3-seragam, kami menunjukkan bahwa jumlah lazy burning kuadrat Latin adalah satu ditambah rantai subkuadrat terhubung terpendeknya. Kami menentukan jumlah lazy burning kuadrat Latin yang berasal dari grup yang dihasilkan secara terbatas. Kami selesai dengan masalah terbuka.
1 Pendahuluan
Pembakaran grafik adalah model sederhana untuk penyebaran pengaruh dalam suatu jaringan. Proses ini terkait dengan parameter yang diperkenalkan dalam [ 1 , 2 ], yaitu nomor pembakaran, yang mengukur kecepatan penyebaran pengaruh ke setiap simpul. Diberikan sebuah grafikpersamaan matematika, proses pembakaran padapersamaan matematikaadalah proses waktu diskrit. Pada awal putaran pertama, semua simpul tidak terbakar. Pada setiap putaran, pertama-tama, semua simpul yang tidak terbakar yang memiliki tetangga yang terbakar akan terbakar, dan kemudian satu simpul baru yang tidak terbakar dipilih untuk dibakar jika simpul tersebut tersedia. Jumlah pembakaranpersamaan matematika, tertulispersamaan matematika, didefinisikan sebagai yang paling sedikitpersamaan matematikasehingga setelahpersamaan matematikaputaran, setiap titik sudutnyapersamaan matematikaterbakar. Untuk informasi lebih lanjut tentang pembakaran grafik, lihat survei [ 3 ] dan buku [ 4 ].
Untuk bilangan bulat positifpersamaan matematika, sebuah kotak Latin dengan urutan persamaan matematikaadalah sebuahpersamaan matematikasusunan sel, dengan setiap sel berisi simbol dari satu setpersamaan matematikadenganpersamaan matematika, sehingga setiap simbol muncul tepat satu kali di setiap baris dan di setiap kolom. Entri dari kotak Latin adalah tripelmathematical equation, dimana simbolmathematical equationterjadi di sel barismathematical equationdan kolommathematical equation. Akan lebih mudah untuk menuliskan kotak Latin sebagai himpunan semua entrinya. Pembakaran didefinisikan melalui perambatan pada sisi-sisi dalam grafik, jadi pertanyaan yang wajar adalah bagaimana mendefinisikannya secara efisien untuk kotak Latin. Grafik kotak Latin dari kotak Latinmathematical equationsesuai pesananmathematical equationadalah grafik denganmathematical equationsimpul yang diberi label dengan sel-sel kotak Latin, di mana simpul-simpul yang berbeda berdekatan jika mereka berbagi baris, kolom, atau simbol. Nomor pembakaran grafik kotak Latin maksimal 3, yang membatasi potensinya untuk perilaku yang lebih rumit atau bervariasi. Pendekatan kami adalah mempertimbangkan pembakaran berbagai hipergraf yang dibangun dari kotak Latin. Kami akan mempertimbangkan aturan propagasi untuk pembakaran pada hipergraf dengan memanfaatkan hipertepi yang menghasilkan hasil yang lebih halus.
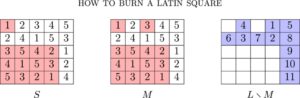
Pertama, kami menyediakan beberapa latar belakang dan notasi pada kotak Latin dan hipergraf; lihat Gambar 1 untuk contoh kotak Latin. Kami menulismathematical equationjikamathematical equationadalah sebuah entri darimathematical equationdan menunjukkan set entri darimathematical equationsebagaimathematical equation, masing-masing. Baris-baris persegi Latin dengan urutanmathematical equationadalahmathematical equation-set entri dalammathematical equationdalam baris tertentu. Garis kolom dan garis simbol didefinisikan dengan cara yang sama. Kita menyebut garis baris, garis kolom, dan garis simbol secara kolektif sebagai garismathematical equationdan mendefinisikanmathematical equationmenjadi himpunan semua garismathematical equation. Sebuah subpersegi dari persegi Latinmathematical equationadalah kotak latin, katakanlahmathematical equation, yang terkandung dalammathematical equationsehinggamathematical equation. Sebuah subpersegimathematical equationdarimathematical equationadalah hal yang sepele jikamathematical equationatau jikamathematical equationmemiliki satu entri dan tepat , jika tidak.


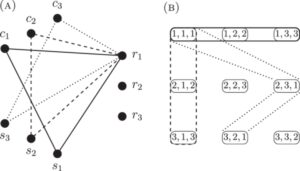



Penutup untuk kotak Latin diperkenalkan pada [ 11 ] sebagai cara untuk mempelajari transversal parsial, topik yang dipelajari secara ekstensif di bidang kotak Latin. Memikirkan setiap baris dan setiap kolom kotak Latin sebagai permutasi, kotak Latin adalah ganjil jika ada sejumlah ganjil permutasi ganjil yang direpresentasikan di antara baris dan kolom kotak Latin dan genap sebaliknya. Dugaan Ryser-Brualdi-Stein yang terkenal menanyakan apakah semua kotak Latin genap memiliki transversal parsial berukuran
dan apakah semua kotak Latin ganjil memiliki transversal. Sejumlah penulis telah berkontribusi pada masalah ini [ 18 – 23 ], dan pracetak baru-baru ini mengklaim telah menyelesaikannya [ 24 ]. Untuk kotak Latin yang merupakan tabel Cayley dari suatu grup, dugaan Hall-Paige [ 25 ] menanyakan apakah kondisi tertentu cukup untuk menjamin bahwa kotak Latin tersebut berisi transversal, yang setara dengan adanya pemetaan lengkap dari grup tersebut. Ini dikonfirmasi dalam [ 26 , 27 ].
Konsep lain yang berguna untuk kotak Latin adalah apakah kotak Latin dapat didekomposisi menjadi transversal, yang terkait erat dengan ortogonalitas kotak Latin; lihat [ 28 ]. Karena hubungan yang begitu penting, sejumlah struktur yang terkait erat dengan transversal menjadi objek yang menarik, termasuk
-plexes [ 29 – 31 ] dan cover [ 11 ]. Latin square yang berisi berbagai panjang transversal parsial maksimal juga telah dipelajari [ 32 ]. Ada juga berbagai alternatif untuk ortogonalitas reguler di Latin square [ 33 – 37 ], dan ini dapat menyebabkan struktur yang mirip dengan transversal. Untuk tinjauan literatur terbaru tentang transversal di Latin square, lihat [ 38 ].

Seperti yang baru saja kita tunjukkan, pelengkap dari himpunan pembakaran malas minimal selalu berupa penutup, tetapi tidak setiap penutup dapat diurutkan untuk membentuk urutan penutup; pertimbangkan penutup trivial dari setiap entri
. Namun, kami tunjukkan di bawah bahwa penutup yang diperoleh sebagai pelengkap dari himpunan pembakaran malas minimal dapat diurutkan ke dalam urutan penutup.




Meskipun rantai kotak Latin belum dipelajari dengan baik secara umum, studi subkotak dalam kotak Latin merupakan topik yang sangat menarik. Jumlah subkotak yang diharapkan dalam kotak Latin acak dipelajari dalam [ 39-43 ] . Hasil- hasil ini telah digunakan untuk memberikan hubungan penting dengan pelabelan kanonik kotak Latin dalam [ 40 ]. Kotak Latin dengan subkotak terpisah dengan ukuran yang ditentukan telah dipelajari [ 44 , 45 ], seperti halnya kotak Latin di mana setiap entri muncul dalam subkotak yang tepat [ 46 ]. Subgrup dari grup sesuai dengan subkotak dari Tabel Cayley yang sesuai dari kotak Latin, dan banyak hubungan menarik ada di sini; lihat [ 32 ].


Selanjutnya kita peroleh batas atas Teorema 6 , yang melengkapi pembuktian teorema tersebut.






3 Membakar Kasus 3 Seragam






Hasil di bawah ini mengikuti langsung dari Teorema 19 .

Karena kami terutama berfokus pada varian pembakaran yang malas, akan menarik untuk mengeksplorasi versi pembakaran berbasis bulat pada hipergraf yang muncul dari kotak Latin. Akan menarik juga untuk mengeksplorasi pembakaran berbasis malas dan bulat pada keluarga hipergraf lainnya, seperti yang muncul dari kotak Latin atau persegi panjang Latin yang saling ortogonal.
Kami mengeksplorasi sejumlah struktur baru yang terkait dengan Latin square, seperti rantai subsquare yang terhubung dan cover-sequences. Meskipun konsep-konsep ini terutama digunakan sebagai alat untuk mempelajari lazy hypergraph burning, kami pikir konsep-konsep ini menjanjikan untuk dipelajari dengan caranya sendiri.