Bagian pertama yang baru, Pendahuluan , telah ditambahkan, yang memberikan klarifikasi berikut. Penambahan ini mengubah penomoran bagian-bagian berikutnya.

Penyerapan nanopartikel (NP) seluler diteliti untuk tujuan penghantaran obat. Yang terakhir ditempelkan pada NP dan dihantarkan ke sel. Obat-obatan ini bertujuan, tergantung pada pengobatannya, untuk membunuh atau mengubah fungsi sel. Terapi semacam itu saat ini digunakan dan mengalami pertumbuhan eksponensial untuk pengobatan kanker [1]. Oleh karena itu, sangat penting untuk mengkalibrasi NP dengan benar agar dapat menargetkan sel secara efisien dan menghindari kerusakan pada sel yang sehat. Cara menargetkan sel kanker dapat bersifat biokimia atau bahkan mekanis. Dalam kasus kedua, NP dirancang untuk memanfaatkan perbedaan signifikan yang diamati antara sifat mekanis sel sehat dan sel kanker [2–4]. Misalnya, perbandingan antara sel payudara M10 dan MCF7 menunjukkan bahwa sel kanker mamalia lebih lunak daripada sel sehat [3, 5–7]. Untuk memahami dengan benar fenomena dan parameter yang mendorong penghantaran obat yang dikontrol secara mekanis, penyelidikan eksperimental dan numerik telah dilakukan. Dalam karya kami sebelumnya, yang difokuskan pada pengiriman obat melalui penyerapan selular endositosis, kami mengusulkan sebuah metode, berdasarkan model penyerapan selular NP yang ada [8], untuk kuantifikasi pengaruh rasio aspek NP, adhesi sel NP dan tegangan membran sel pada penyerapan NP [9]. Kemudian, kami menyajikan model yang disempurnakan yang memperhitungkan respons mekanis membran sel selama pembungkusan NP oleh membran dan kami menunjukkan bahwa prediksi model diubah ketika mempertimbangkan respons mekanis ini [10]. Namun, pengaruh parameter awal sistem tidak dapat dibandingkan dengan yang mewakili respons mekanis membran karena kompleksitas dan biaya komputasi dari pendekatan tersebut. Dengan demikian, tujuan dari artikel ini adalah untuk membangun model pengganti untuk mengevaluasi indeks sensitivitas (indeks Sobol) yang menggambarkan pengaruh parameter masukan model pada prediksinya. Garis besar artikel ini adalah sebagai berikut. Bagian 2 memperkenalkan model, yang deskripsi lengkapnya disediakan dalam [9, 10]. Selanjutnya, strategi untuk membangun model pengganti, menggunakan pendekatan Kriging, Polynomial Chaos Expansion (PCE), dan pembelajaran mendalam, disajikan pada Bagian 3. Analisis sensitivitas selanjutnya dilakukan pada Bagian 4.

Pada baris ke-4 bagian Penyajian model , setelah frasa yang diakhiri dengan “sebagaimana dirinci pada angka 9”, kami telah menambahkan kalimat berikut:

Yang terakhir disebabkan oleh kontribusi energi yang diperlukan untuk menekuk membran di sekitar NP (kontribusi positif), energi yang diperlukan untuk meregangkan membran (kontribusi positif) dan energi yang dilepaskan oleh adhesi antara NP dan membran (kontribusi negatif). Posisi kesetimbangan sistem didefinisikan sebagai minimum lokal pertama (yaitu, yang ditemui paling awal selama proses pembungkusan) dari energi potensial, karena telah ditunjukkan dalam literatur bahwa tidak ada fenomena eksternal yang mampu membuat sistem meninggalkan posisi ini [1].

Di tengah paragraf yang sama, setelah “Geometri NP adalah”, kami menambahkan kata “didefinisikan.” Awal frasa tersebut ditulis sebagai berikut: Geometri NP didefinisikan oleh rasio aspeknya ….

Di akhir baris keempat subbagian Definisi set data masukan (yaitu, setelah frasa yang diakhiri dengan “melalui variabel acak”), kami menambahkan: Berdasarkan konvensi umum dalam statistik dan probabilitas, dalam makalah kami huruf kapital (misalkan X) menunjukkan variabel acak sementara nilainya dilambangkan dengan huruf kecil (misalkan x). Dengan demikian, variabel acak didefinisikan sebagai berikut ….

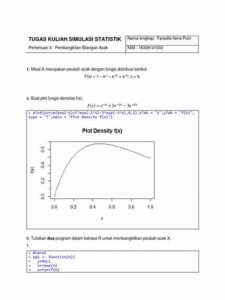
Lima baris berikutnya, kami membuat perubahan ini: Fungsi Kepadatan Probabilitas (PDF) yang sesuai disediakan di [10].

Pada paragraf berikutnya, setelah baris keenam (diakhiri denganpersamaan matematika), kami menambahkan kalimat berikut:

Untuk memahami makna fisik dari puncak-puncak ini, perlu untuk menggambarkan kontribusi terhadap energi potensial total sistem yang disajikan dan dibahas secara rinci dalam artikel pertama kami [9] dan diingat kembali secara singkat di Bagian 2. Menimbang bahwa kumpulan data berisi NP horizontal dan vertikal yang sedikit hingga sangat memanjang, orang dapat memperkirakan energi tekukan yang diperlukan untuk membungkus membran di sekitar NP sangat bervariasi di antara sampel. Energi tekukan ini bergantung pada kelengkungan NP yang dekat dengan membran. Misalnya, dalam kasus NP vertikal yang memanjang, tekukan penting diperlukan, yang melibatkan istilah positif besar dalam energi potensial total sistem, sehingga mendorong minimum lokal pertama mendekati nol. Inilah alasan mengapa puncak pertama terutama dapat dikaitkan dengan NP vertikal yang memanjang, yang memerlukan tekukan membran yang signifikan dan intensif energi.

Paragraf ini diakhiri dengan baris yang telah dimodifikasi sebagai berikut: Puncak terakhir dipersamaan matematikaberkaitan dengan kasus-kasus di mana pembungkusan tidak terhalang secara signifikan oleh NP yang sangat memanjang, atau di mana parameter adhesi cukup besar untuk mengimbangi pembengkokan.

Pada baris ketujuh dari subbagian Kriging dan metamodel ekspansi kekacauan polinomial , kami telah menambahkan kata “test” dalam frasa ini: Berdasarkan hasil ini, 10% dari kumpulan data (409 sampel) akan digunakan untuk menguji metamodel, dan 90% sisanya, yaitu 3687 sampel, akan digunakan untuk pelatihannya.

Pada subbagian yang sama, di akhir paragraf kedua, kami telah menambahkan “distribusi mode tunggal yang terletak di
” pada frasa yang dimulai dengan “Selain itu, model Kriging menghasilkan.” Pada subbagian yang sama, baris kedua setelah Persamaan (2), setelah frasa yang diakhiri dengan “menunjukkan ukuran dataset dan Var adalah varians,” kami telah menambahkan frasa berikut: Faktor prediktivitas berkisar antara 0 dan 1. Semakin dekat ke 1, semakin akurat prediksinya.

Pada subbagian Jaringan Syaraf Tiruan , paragraf kedua, baris kedelapan, kami telah mengubah frasa sebagai berikut:
Nilai-nilai dievaluasi menggunakan validasi silang sebanyak 5 kali, setiap kali berisi 736 sampel.

Pada paragraf yang sama, setelah kalimat terakhir yang diakhiri dengan “terlepas dari arsitekturnya,” kami menambahkan: Namun, arsitektur (8, 8, 8) memberikan prediksi paling akurat, sehingga menghasilkan
.

Bahasa Indonesia: Di bagian Diskusi , kami telah menambahkan blok teks ini di awal: Hasil analisis sensitivitas cocok dengan kesimpulan awal yang diperoleh di artikel kami sebelumnya [9, 10]: rasio aspek NP adalah parameter yang paling penting dan variasi adhesi NP-membran perlu diperhitungkan, meskipun memainkan peran sekunder dalam proses pembungkusan. Pentingnya rasio aspek NP, adhesi awal NP-membran dan tegangan membran sudah dikenal dalam literatur, melalui investigasi eksperimental dan numerik [8, 37]. Lebih jauh, analisis sensitivitas yang disajikan dalam artikel dilakukan melalui indeks Sobol, yang umumnya digunakan untuk analisis sensitivitas global. Namun, nilai Shapley lebih sering digunakan dalam komunitas pembelajaran mesin dan mungkin tampak lebih cocok untuk investigasi ANN. Kedua indeks dapat digunakan untuk interpretasi sensitivitas model yang disajikan dalam artikel ini [38]. Hasil nilai Shapley menghasilkan kesimpulan yang sama dengan yang diperoleh dari indeks Sobol. Oleh karena itu, hasil-hasil ini lebih disukai tidak disajikan dalam artikel, tetapi dapat ditemukan dalam Materi Informasi Pendukung.

Di bagian yang sama, setelah frasa yang diakhiri dengan “Prediksi indeks Sobol belum dikuantifikasi,” kami menambahkan: Lebih jauh, penting untuk dicatat bahwa indeks sensitivitas Sobol yang dievaluasi dalam artikel ini memberikan informasi tentang sensitivitas model ANN terhadap parameter input, alih-alih secara langsung mencerminkan sensitivitas fenomena biologis atau model itu sendiri. Oleh karena itu, hasil ini harus divalidasi secara eksperimental dan hanya dapat berfungsi sebagai panduan awal.

Bagian Informasi Pendukung juga telah dimodifikasi sebagai berikut: Kode Python yang berisi model penyerapan seluler NP elips kaku, bersama dengan rutinitas untuk mendapatkannya
, tersedia di repositori Github ini: https://github.com/SarahIaquinta/ANN-sensitivity-adaptive-uptake-of-elliptic-nanoparticles . Repositori ini juga berisi data dan metode yang digunakan untuk mengimplementasikan dan memvalidasi metamodel dan jaringan saraf tiruan, serta algoritme yang digunakan untuk menghitung indeks sensitivitas (indeks Sobol dan nilai Shapley).

Secara total, sembilan referensi baru telah ditambahkan. Berikut adalah daftar referensi baru, dengan entri bernomor:

1. Y. Dang dan J. Guan, “Sistem Pengiriman Obat Berbasis Nanopartikel untuk Terapi Kanker,” Smart Materials in Medicine 1 (2020): 10–19.
2. M. Lekka, K. Pogoda, J. Gostek J, dkk., “Pengenalan Sel Kanker—Fenotipe Mekanik,” Micron 43, no. 12 (2012): 1259–1266.
3. HH Lin, HK Lin, IH Lin, dkk., “Fenotipe Mekanis Sel Kanker: Pelunakan Sel dan Hilangnya Penginderaan Kekakuan,” Oncotarget 6, no. 25 (2015): 20946–20958.
4. Y. Hui, X. Yi, F. Hou, dkk., “Peran Sifat Mekanik Nanopartikel dalam Pengiriman Obat Kanker,” ACS Nano 13, no. 7 (2019): 7410–7424.
5. C. Handel, BS Schmidt, J. Schiller, dkk., “Pelunakan Membran Sel pada Sel Kanker Payudara dan Serviks Manusia,” Jurnal Fisika Baru 17, no. 8 (2015): 083008.
6. M. Lekka, D. Gil, K. Pogoda, dkk., “Deteksi Sel Kanker pada Potongan Jaringan Menggunakan AFM,” Arsip Biokimia dan Biofisika 518, no. 2 (2012): 151–156.
7. Q. Li, GY Lee, CN Ong, dan CT Lim, “Studi Indentasi AFM pada Sel Kanker Payudara,” Komunikasi Penelitian Biokimia dan Biofisika 374, no. 4 (2008): 609–613.
8. X. Yi, X. Shi, dan H. Gao, “Penyerapan Seluler Nanopartikel Elastis,” Physical Review Letters 107, no. 9 (2011): 098101.
9. S. Iaquinta, S. Khazaie, E. Ishow, C. Blanquart, S. Freour, dan F. Jacquemin, “Pengaruh Parameter Mekanik dan Geometris pada Penyerapan Seluler Nanopartikel: Pendekatan Stokastik,” Jurnal Internasional untuk Metode Numerik dalam Teknik Biomedis 38, no. 6 (2022): e3598.
10. S. Iaquinta, S. Khazaie, S. Freour, dan F. Jacquemin, “Akuntansi untuk Respons Mekanis Membran Sel Selama Penyerapan Nanopartikel Acak,” Jurnal Mekanika Teoretis dan Komputasi .
11. M. Deserno dan T. Bickel, “Pembungkusan Koloid Bulat dengan Membran Fluida,” Europhysics Letters 62, no. 5 (2003): 767–773.
12. U. Seifert dan R. Lipowsky, “Adhesi Vesikel,” Physical Review A 42, no. 8 (1990): 4768–4771.
13. S. Zhang, H. Gao, dan G. Bao, “Prinsip Fisik Endositosis Seluler Nanopartikel,” ACS Nano 9, no. 9 (2015): 8655–8671.
14. T. Briolay, T. Petithomme, M. Fouet, N. Nguyen-Pham, C. Blanquart, dan N. Boisgerault, “Penyampaian Terapi Kanker melalui Nanovektor Sintetis dan Terinspirasi Biologi,” Molecular Cancer 20, no. 1 (2021): 1–24.
15. ET Jaynes, “Teori Informasi dan Mekanika Statistik,” Physical Review 106, no. 4 (1957): 620–630.
16. M. Baudin, A. Dutfoy, B. Iooss, dan AL Popelin, OpenTURNS: Perangkat Lunak Industri untuk Kuantifikasi Ketidakpastian dalam Simulasi (Springer International Publishing, 2016), 1–38.
17. Y. LeCun, Y. Bengio, dan G. Hinton, “Pembelajaran Mendalam,” Nature 521, no. 7553 (2015): 436–444, https://doi.org/10.1038/nature14539 .
18. F. Pedregosa, G. Varoquaux, A. Gramfort, dkk., “Scikit-Learn: Pembelajaran Mesin dalam Python,” Jurnal Penelitian Pembelajaran Mesin 12 (2011): 2825–2830.
19. B. Iooss dan P. Lemaitre, “Tinjauan tentang Metode Analisis Sensitivitas Global,” dalam Manajemen Ketidakpastian dalam Simulasi-Optimasi Sistem Kompleks: Algoritma dan Aplikasi , ed. C. Meloni dan G. Dellino (Springer, 2015).
20. H. Christopher Frey dan SR Patil, “Identifikasi dan Tinjauan Metode Analisis Sensitivitas,” Analisis Risiko 22, no. 3 (2002): 553–578.
21. MF Alam dan A. Briggs, “Metamodel Jaringan Syaraf Tiruan untuk Analisis Sensitivitas dalam Model Ekonomi Kesehatan Penggantian Pinggul Total,” Tinjauan Pakar Farmakoekonomi & Penelitian Hasil 20, no. 6 (2020): 629–640.
22. M. Ghorbanzadeh, MH Fatemi, dan M. Karimpour, “Pemodelan Penyerapan Seluler Nanopartikel Magnetofluoresens dalam Sel Kanker Pankreas: Studi Hubungan Struktur Aktivitas Kuantitatif,” Penelitian Kimia Industri & Teknik 51, no. 32 (2012): 10712–10718.
23. J. Morio, “Metode Analisis Sensitivitas Global dan Lokal untuk Sistem Fisik,” Jurnal Fisika Eropa 32, no. 6 (2011): 1577–1588.
24. O. Asserin, A. Loredo, M. Petelet, dan B. Iooss, “Analisis Sensitivitas Global dalam Simulasi Pengelasan—Apa Saja Data Material yang Benar-Benar Anda Butuhkan?” Finite Elements in Analysis and Design 47, no. 9 (2011): 1004–1016.
25. A. Saltelli, M. Ratto, T. Andres, dkk., Analisis Sensitivitas Global: Primer (John Wiley & Sons, 2008).
26. A. Saltelli, S. Tarantola, F. Campolongo, dan M. Ratto, Analisis Sensitivitas dalam Praktik: Panduan untuk Menilai Model Ilmiah (Perpustakaan Daring Wiley, 2004).
27. B. Iooss, L. Boussouf, V. Feuillard, dan A. Marrel, “Studi Numerik tentang Proses Penyesuaian dan Validasi Metamodel,” arXiv Preprint (2010): arXiv:1001.1049.
28. IM Sobol, “Analisis Sensitivitas untuk Model Matematika Non-Linear.” Pemodelan Matematika dan Eksperimen Komputasi 1 (1993): 407–414.
29. S. Marelli, C. Lamas, K. Konakli, dkk., Panduan Pengguna UQLab – Analisis Sensitivitas. Laporan Teknis, Ketua Kuantifikasi Risiko, Keselamatan, dan Ketidakpastian (UQLab, 2021).
30. A. Saltelli, “Memanfaatkan Evaluasi Model Sebaik-baiknya untuk Menghitung Indeks Sensitivitas,” Computer Physics Communications 145, no. 2 (2002): 280–297.
31. S. Tarantola, D. Gatelli, SS Kucherenko, dkk., “Memperkirakan Kesalahan Aproksimasi Saat Memperbaiki Faktor-Faktor yang Tidak Penting dalam Keandalan Analisis Sensitivitas Global,” Engineering & System Safety 92, no. 7 (2007): 957–960, https://doi.org/10.1016/j.ress.2006.07.001 .
32. JM Martinez, “Analisis de sensibilite globale par decomposition de la variance,” Journee des GdR Ondes & Mascot 13 (2011).
33. MJW Jansen, “Analisis Desain Varians untuk Output Model,” Komunikasi Fisika Komputer 117, no. 1–2 (1999): 35–43.
34. PA Vanrolleghem, G. Mannina, A. Cosenza, dan MB Neumann, “Analisis Sensitivitas Global untuk Pemodelan Kualitas Air Perkotaan: Terminologi, Konvergensi, dan Perbandingan Berbagai Metode,” Jurnal Hidrologi 522 (2015): 339–352.
35. JD Herman, JB Kollat, PM Reed, dan T. Wagener, “Metode Morris Secara Efektif Mengurangi Permintaan Komputasi Analisis Sensitivitas Global untuk Model Daerah Aliran Sungai Terdistribusi,” Hidrologi dan Ilmu Sistem Bumi 17, no. 7 (2013): 2893–2903.
36. F. Sarrazin, F. Pianosi, dan T. Wagener, “Analisis Sensitivitas Global Model Lingkungan: Konvergensi dan Validasi,” Environmental Modelling & Software 79 (2016): 135–152.
37. JA Champion dan S. Mitragotri, “Peran Geometri Target dalam Fagositosis,” Prosiding Akademi Ilmu Pengetahuan Nasional 103, no. 13 (2006): 4930–4934.
38. B. Vuillod, M. Montemurro, E. Panettieri, dan L. Hallo. “Perbandingan Antara Indeks Sobol dan Efek Shapley untuk Analisis Sensitivitas Global Sistem dengan Variabel Input Independen,” Reliability Engineering & System Safety 234 (2023): 109177.