ABSTRAK
Persamaan Diferensial Biasa (ODE) Neural merupakan kemajuan signifikan di persimpangan pembelajaran mesin dan sistem dinamis, yang menawarkan analog waktu kontinu untuk jaringan saraf diskrit. Meskipun menjanjikan, penerapan ODE neural dalam aplikasi praktis sering kali menghadapi tantangan kekakuan, suatu kondisi di mana variasi cepat dalam beberapa komponen solusi menuntut langkah waktu yang sangat kecil untuk penyelesai eksplisit. Karya ini membahas masalah kekakuan saat menggunakan ODE neural untuk reduksi orde model dengan memperkenalkan reparametrisasi yang sesuai dalam waktu. Pemetaan yang dipertimbangkan digerakkan oleh data, dan diinduksi oleh langkah waktu adaptif dari penyelesai implisit pada solusi referensi. Kami menunjukkan bahwa pemetaan menghasilkan sistem yang tidak kaku yang dapat diselesaikan dengan mudah dengan skema integrasi waktu eksplisit. Dinamika waktu kaku asli dipulihkan melalui pemetaan yang dipelajari oleh jaringan saraf yang menghubungkan ruang keadaan ke reparametrisasi waktu. Kami memvalidasi metode kami melalui eksperimen ekstensif, menunjukkan peningkatan efisiensi untuk inferensi ODE saraf sambil mempertahankan ketahanan dan akurasi jika dibandingkan dengan penyelesai implisit yang diterapkan pada sistem kaku dengan sisi kanan asli.

1 Pendahuluan
Dalam ilmu komputasi dan rekayasa, kompleksitas dan skala simulasi numerik telah tumbuh secara eksponensial, didorong oleh kemajuan dalam perangkat keras dan algoritma. Model fidelitas tinggi—juga disebut Full Order Models (FOMs)—sekarang dapat menangkap detail rumit dari fenomena fisik di berbagai domain seperti dinamika fluida, analisis struktural, pemodelan iklim, dan ilmu material. Namun, meningkatnya kompleksitas model-model ini sering kali disertai dengan biaya komputasi yang signifikan, sehingga tidak praktis untuk banyak aplikasi yang memerlukan evaluasi model berulang atas sejumlah besar nilai parameter. Memang, biaya komputasi didorong oleh kutukan dimensionalitas [ 1 ].

Reduced-Order Models (ROMs) telah muncul sebagai solusi yang ampuh untuk tantangan ini, menawarkan keseimbangan antara akurasi dan efisiensi komputasi. Dengan mengompresi fitur-fitur penting FOM ke dalam bentuk yang lebih mudah dikelola, yang biasanya disebut ruang laten, ROM memungkinkan simulasi dan analisis sistem yang kompleks secara efisien, terutama yang memerlukan analisis waktu nyata [ 2 ], masalah invers [ 3 – 6 ], kuantifikasi ketidakpastian [ 7 – 9 ], optimasi bentuk [ 10 ] atau kontrol optimal [ 11 – 13 ].

Bidang ROM telah mengalami pertumbuhan yang signifikan, menyediakan berbagai macam teknik yang dapat dipilih oleh para praktisi. Setiap metode memiliki serangkaian kelebihan dan kekurangannya sendiri, dan pilihan ROM yang optimal sering kali bergantung pada persyaratan khusus aplikasi. Memang, istilah ROM mengacu pada beberapa pendekatan, yang agak berbeda satu sama lain.

Salah satu paradigma yang paling mapan untuk reduksi orde model adalah dekomposisi ortogonal yang tepat (POD) [ 14 , 15 ], yaitu, teknik proyeksi linier yang memberikan tingkat kompresi tinggi dan, misalnya, mencapai tingkat akurasi yang sangat tinggi dalam kasus proses difusi.

Jika persamaan yang mengatur model fidelitas tinggi secara eksplisit digunakan dalam ROM, mereka disebut intrusif [ 16 – 20 ]. Biasanya, algoritma greedy atau POD digunakan untuk memproyeksikan FOM ke ruang berdimensi lebih rendah. Namun, untuk model nonlinier, teknik tambahan seperti metode interpolasi empiris (diskrit) diperlukan untuk menangani kompleksitas, yang dapat menyebabkan tradeoff yang tidak menguntungkan antara akurasi dan efisiensi komputasi [ 21 – 23 ] . Selain itu, dalam [ 24 ] telah ditunjukkan bahwa untuk masalah yang didominasi transportasi, dimensi laten yang besar harus digunakan untuk mencapai akurasi yang wajar saat menggunakan POD, sehingga membatasi penggunaan praktisnya.

Dalam beberapa tahun terakhir, metode berbasis data berdasarkan pembelajaran mesin dan pembelajaran mendalam telah memperoleh daya tarik besar karena kemajuan dalam perangkat keras berbasis GPU dan pengembangan dalam algoritma dan perangkat lunak yang mendukung ekosistem kecerdasan buatan. Paradigma ini didasarkan pada ketersediaan sejumlah besar data fidelitas tinggi yang dapat digunakan untuk melatih model. Pendekatan ini terbukti efektif jika sejumlah besar sumber daya yang digunakan dalam fase offline (pembuatan solusi dan pelatihan model) dibayar kembali oleh sejumlah besar evaluasi (murah) dari model yang dilatih (fase online). Model-model ini disebut non-intrusif karena hanya pengetahuan tentang data yang diperlukan untuk membangunnya [ 25 , 26 ]. Kami juga menyebut ROM jenis ini sebagai model pengganti, mengingat kemampuannya untuk memperkirakan perilaku FOM asli dari data. Bidang ini terus berkembang, dengan sejumlah besar teknik yang dikembangkan dan diterbitkan. Sejauh pengetahuan kami, contoh pendekatan berbasis data yang paling relevan adalah sebagai berikut. Model penutupan adalah hibrida antara POD dan pendekatan berbasis data di mana istilah nonlinier (jaringan saraf) ditambahkan ke ROM linier (biasanya POD-Galerkin) untuk memperhitungkan efek dinamika yang belum terselesaikan [ 27 ]. Dalam [ 28 – 32 ], autoencoder yang terhubung rapat atau konvolusional telah digunakan untuk mengekstraksi variabel laten penuh. Teknik lain telah diusulkan untuk meningkatkan akurasi. Misalnya, jaringan saraf grafik (GNN) mengatasi masalah geometri rumit yang didiskritkan dengan jaring tak terstruktur, menawarkan representasi variabel yang lebih alami menggunakan grafik [ 33 , 34 ]. Operator saraf Fourier adalah pendekatan yang sangat sukses yang malah mengeksploitasi ruang frekuensi untuk memperkaya lapisan model [ 35 – 37 ]. Tergantung pada model yang dipertimbangkan, evolusi waktu dapat diperlakukan seperti parameter sistem lainnya atau dipelajari secara eksplisit, contohnya adalah DeepONets [ 31 , 38 ], dekomposisi mode dinamis [ 39 , 40 ], identifikasi jarang dinamika laten tereduksi (SINDy) [ 41 , 42 ], RNN [ 43 ], LSTM [ 32 , 44 ] atau proses Gaussian [ 45 ].

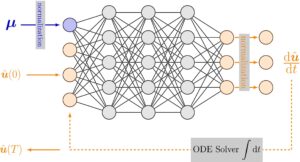
Pendekatan evolusi waktu lain yang menarik adalah yang berbasis pada neural ODE [ 46-49 ]. Konsep inti dari metode ini sederhana: metode ini melibatkan pembelajaran sisi kanan sistem dinamis dengan jaringan saraf padat, yang dapat dilihat sebagai limit kontinu dari jaringan saraf residual. Pendekatan ini menawarkan banyak keuntungan, termasuk representasi data waktu kontinu yang lebih alami dan peningkatan efisiensi parameter dan memori. Tantangan utama dengan neural ODE adalah bahwa pada dasarnya, mereka adalah ODE yang harus dipecahkan. Hal ini sering menimbulkan masalah dengan kekakuan, yang memperumit solusi mereka dan berpotensi memengaruhi stabilitas dan akurasinya. Kekakuan adalah kondisi di mana ada perubahan cepat pada beberapa komponen solusi sementara komponen lain berubah perlahan. Fenomena ini menciptakan tantangan numerik saat memecahkan persamaan, karena metode numerik eksplisit mungkin menjadi tidak efisien atau tidak stabil [ 50 ]. Dengan demikian, kebutuhan untuk menggunakan penyelesai implisit secara signifikan meningkatkan biaya.

Dalam karya ini, kami menangani masalah membangun ROM dari sistem yang kaku. Dalam kasus ini, hambatan utama tidak diwakili oleh sejumlah besar variabel sistem tetapi oleh kekakuan sistem. Memang, ada beberapa jenis kekakuan, yang biasanya terhubung ke fitur sistem, seperti keberadaan beberapa skala waktu, spektrum Jacobian sistem, atau ketidakstabilan numerik, yang membuat pembangunan ROM menjadi tugas yang menantang. Dalam hal ini, menggunakan time-stepper waktu tetap tidak layak karena skala yang berubah dengan cepat memerlukan langkah-langkah yang sangat kecil. Di sisi lain, memperlakukan waktu seperti input jaringan saraf padat juga terbukti bermasalah karena jaringan saraf diketahui berkinerja buruk pada frekuensi tinggi [ 51 ]. Namun, dalam literatur, dapat ditemukan beberapa contoh masalah kaku yang diselesaikan dengan pembelajaran mesin. Solusi yang mungkin pertama kali diajukan dalam [ 52 ], di mana penulis menggunakan asumsi quasi-steady-state (QSSA) untuk mengurangi kekakuan sistem ODE dan menunjukkan bahwa jaringan saraf yang diinformasikan fisika (PINN) kemudian dapat berhasil diterapkan pada sistem non-/mild-kaku yang dikonversi. Ini sangat menarik karena sistem dapat dipecahkan dengan metode eksplisit. Dalam [ 53 ], penulis menunjukkan bahwa menghitung gradien yang distabilkan dan penskalaan yang sesuai dari keluaran jaringan memungkinkan pembelajaran ODE saraf kaku. Dalam [ 54 ], PINN digunakan dengan mesin pembelajaran ekstrem untuk memecahkan masalah kaku. Dalam [ 55 ], model farmakologi sistem kuantitatif kaku dipercepat dengan jaringan status gema. Dalam [ 56 ], autoencoder digunakan untuk menghasilkan ROM model kinetika kimia untuk simulasi sistem pembakaran. Baru-baru ini, dalam [ 57 ] DeepONets digunakan untuk mempelajari solusi terdiskritisasi dari kinetika kimia kaku yang menantang.

Strategi kami adalah menggunakan ODE neural berbasis non-stiff surrogate untuk dinamika kaku. Yaitu, kami bertujuan untuk menggunakan ODE neural untuk mempelajari sistem kaku yang diparameterisasi ulang waktu, di mana peta waktu dibangun dengan tepat untuk mengurangi kekakuan masalah. Wawasannya adalah untuk mengeksploitasi keuntungan dari ODE neural yang kami jelaskan sebelumnya sambil menjaga biaya (online) untuk memecahkan ODE di bawah kendali dengan menggunakan penyelesai eksplisit. Memang, kontribusi utama kami adalah menggunakan reparametrisasi waktu yang disebabkan oleh langkah waktu penyelesai implisit sebagai cara untuk mengurangi kekakuan sistem. Keuntungan dari prosedur ini adalah bahwa hal itu murni digerakkan oleh data, yang berarti bahwa adalah mungkin untuk menghindari secara manual memperoleh ekspresi aljabar eksplisit untuk spesies QSS seperti yang dilakukan dalam [ 52 ]. Di sisi lain, kelemahan dari pendekatan kami adalah bahwa hal itu hanya bermanfaat untuk ROM: fase pengumpulan data yang mahal untuk membangun pemetaan waktu harus diimbangi dengan fase online yang murah. Teknik kami juga dapat diartikan sebagai cara untuk menanamkan langkah waktu adaptif (implisit) langsung ke dalam ODE saraf. Dengan demikian, kita dapat menghindari backpropagation melalui penyelesai implisit, yang menimbulkan biaya kubik sehubungan dengan jumlah parameter jaringan saraf [ 53 ], sehingga sangat mengurangi biaya komputasi untuk melatih ODE saraf. Strategi reparametrisasi kami juga terhubung dengan [ 58 – 60 ], di mana penulis memanfaatkan pemetaan spasial untuk penyempurnaan mesh adaptif untuk meningkatkan efisiensi komputasi dan untuk meningkatkan representasi dinamika nonlinier dalam sistem yang kompleks. Selain itu, pekerjaan terbaru [ 61 ] telah menunjukkan bahwa NODE yang mempertahankan struktur dengan pemisahan linier/nonlinier dapat mencapai stabilitas jangka panjang pada masalah kaku yang sebanding dengan metode implisit. Setelah sistem yang tidak kaku dipecahkan, solusinya dipetakan kembali ke dinamika kaku menggunakan peta yang dipelajari dengan jaringan saraf. Jaringan saraf dilatih sekali dengan ODE saraf dan menunjukkan sifat generalisasi yang baik ke parameter di luar set data pelatihan. Perhatian khusus diberikan dalam definisi peta sehingga tidak bergantung pada waktu. Oleh karena itu, model mempertahankan generalisasi yang baik dalam waktu untuk sistem periodik karena hanya ada ketergantungan eksplisit pada ruang keadaan.

Teknik kami dirancang khusus untuk masalah di mana kekakuan dapat ditelusuri kembali ke kasus nilai eigen besar dengan bagian riil negatif. Memang, jenis kekakuan lain yang banyak dipelajari adalah kekakuan frekuensi tinggi, yang sesuai dengan kasus nilai eigen yang cukup besar tetapi frekuensi sangat tinggi [ 62 ]. Dalam kasus ini, sistem memiliki solusi cepat dan lambat, di mana solusi cepat harus dipecahkan secara akurat untuk melacak yang lambat. Sementara pendekatan reparametrisasi telah diusulkan [ 63 ], mereka memiliki keterbatasan yang signifikan karena mereka perlu menyelesaikan frekuensi cepat [ 64 , 65 ]. Dengan demikian, jenis kekakuan ini tetap menjadi tantangan bagi pendekatan kami dan area penelitian yang sedang berlangsung. Memang, penulis lain telah mengeksplorasi teknik pembelajaran mesin yang mempertahankan struktur, seperti jaringan saraf cepat-lambat, untuk melewati resolusi langsung transien cepat dalam sistem yang terganggu secara tunggal [ 66 ].

Kami menunjukkan keakuratan dan kecepatan ROM yang diusulkan pada serangkaian lima masalah pengujian, di mana penyelesai eksplisit biasanya gagal, banyak digunakan dalam literatur untuk membandingkan penyelesai ODE kaku [ 67 ]. Hasilnya dibandingkan dengan penyelesai implisit Runge-Kutta terkini dari jenis Radau II A orde kelima [ 50 ] yang diterapkan pada sistem kaku dengan sisi kanan asli.

Sisa dari makalah ini disusun sebagai berikut. Pertama, di Bagian 2 kami memperkenalkan pengaturan dan notasi matematika untuk masalah yang menjadi perhatian. Secara khusus, di Bagian 2.4 kami mengulas pendekatan ODE saraf, yang merupakan dasar dari karya ini. Di Bagian 3 kami memperkenalkan metodologi kami, membahas juga rincian implementasi. Di Bagian 4 kami menyajikan serangkaian hasil numerik yang komprehensif. Akhirnya, di Bagian 5 kami menarik beberapa kesimpulan, membahas kekuatan dan keterbatasan dari pendekatan yang diusulkan.

2 Perumusan Masalah
Pada bagian ini, pertama-tama kami menyajikan konstruksi ROM dalam bentuk aljabar untuk memperkirakan sistem dinamis parametrik. Kemudian, kami memberikan gambaran singkat tentang konsep pembelajaran mendalam yang mendasar dan merumuskan masalah pengurangan orde model berbasis data dalam kerangka kerja ODE neural.

2.1 Sistem Parametrik Persamaan Diferensial Biasa
Kami mempertimbangkan sistem dinamis berparameter dan berdimensi-hingga berikut ini, yang dijelaskan oleh serangkaian ODE orde pertama:

GAMBAR 1 — Contoh manifold solusi diskrit untuk osilator Van der Pol.

GAMBAR 2 — Arsitektur Neural ODE untuk reduksi orde model.

GAMBAR 3 — Perbandingan pendekatan penyelesai ODE dan terbimbing untuk melatih ODE neural dari model yang diinisialisasi secara acak yang sama untuk osilator Van der Pol (lih. Bagian 4.1 ). Biru dan oranye adalah prediksi model, dan hitam adalah solusi referensi. Pelatihan terbimbing secara global kurang akurat dan stabil, tetapi menangkap gradien tajam dengan lebih baik.

GAMBAR 4 — Contoh perilaku kerugian, kerugian validasi, dan laju pembelajaran selama pelatihan ROM dengan pendekatan dua langkah: pertama pendekatan yang diawasi dan kemudian pendekatan penyelesai ODE.

GAMBAR 5 — Alur kerja reparametrisasi waktu. Dimulai dari sistem ODE kaku (berwarna abu-abu), kami menghitung solusi diskrit dan memperoleh manifold diskrit menggunakan metode implisit. Kami menormalkan solusi, menghitung reparameterisasi waktu , dan memperkirakan (berwarna biru). Akhirnya, kita dapat melatih model non-kaku yang dapat diselesaikan menggunakan metode eksplisit (berwarna oranye).

GAMBAR 6 — Kasus uji 1: Osilator Van der Pol. Di sebelah kiri, dalam warna, prediksi ODE saraf di Di sebelah kanan, dalam warna, prediksi dipetakan ke waktu aslinya . Yang berwarna hitam adalah solusi referensi. Garis putus-putus vertikal menunjukkan waktu akhir dalam set data pelatihan.

TABEL 1. Kasus uji 1: Van der Pol.

μ	Pemecah masalah	tol	waktu [s]	# demam	#jev bahasa inggris	# aku	MSE ts	L2	dpeak
1⁢02.01	Bahasa Indonesia: ROM	1/40	0,033	1000	angka 0	angka 0	4.13e-3	0,03520	0.662
	Radau	1⁢0−2	0,046 tahun	tahun 2470	110	516	—	0,01447 pukul 0,01447	0.811
	Radau	1⁢0−1.5	0,041 tahun	tahun 2342	105	482	—	0.37252	pukul 14.59
1⁢02.67	Bahasa Indonesia: ROM	1/40	0,033	1000	angka 0	angka 0	2.39e-3	0,02262	2.665
	Radau	1⁢0−2	0,056 tahun	3316	133	688	—	0,00870	2.075
	Radau	1⁢0−1.5	0,046 tahun	tahun 2591	118	576	—	0.53100	181.5
1⁢03.33	Bahasa Indonesia: ROM	1/40	0,033	1000	angka 0	angka 0	5.94e-3	0,03098	19.27
	Radau	1⁢0−2	0,072	3850	154	tahun 806	—	0,00742 tahun	8.083
	Radau	1⁢0−1.5	0,052	tahun 2992	137	684	—	0.29987	655.2
1⁢03.99	Bahasa Indonesia: ROM	1/40	0,033	1000	angka 0	angka 0	7.23e-3	0,04768 pukul 0,04768	191.0
	Radau	1⁢0−2	0,078 tahun	4418	156	938	—	0,04377 tahun	210.9
	Radau	1⁢0−1.5	0,058	3337	148	768	—	0.17724	tahun 2822

GAMBAR 7 — Kasus uji 2: OREGO. Di sebelah kiri, dalam warna, prediksi ODE saraf di Di sebelah kanan, dalam warna, prediksi dipetakan ke waktu aslinya . Yang berwarna hitam adalah solusi referensi. Skala keadaan adalah logaritmik.

TABEL 2. Kasus uji 2: OREGO.

μ	Pemecah masalah	tol	waktu [s]	# demam	#jev bahasa inggris	# aku	MSE ts	L2	dpeak
(52.5,0.025,1⁢0−5.975)	Bahasa Indonesia: ROM	2·1⁢0−4	0,037 hari	tahun 1130	angka 0	angka 0	1.20e-3	1.19e-2	1.668
	Radau	1⁢0−3	0,065 tahun	3777	167	656	—	1.31e-5	3.032
	Radau	1⁢0−1.5	0,059 tahun	3213	165	664	—	0.4691	6.092
(97.5,0.025,1⁢0−5.975)	Bahasa Indonesia: ROM	2·1⁢0−4	0,034 tahun	tahun 1046	angka 0	angka 0	4.52e-3	7.75e-2	5.041
(97.5,0.025,1⁢0−5.975)	Radau	1⁢0−3	0,067 tahun	3445	159	600	—	2.12e-5	4.632
	Radau	1⁢0−1.5	0,054 tahun	tahun 2815	141	556	—	0,0099	6.574
(52.5,0.175,1⁢0−5.975)	Bahasa Indonesia: ROM	2·1⁢0−4	0,065 tahun	tahun 1970	angka 0	angka 0	2.64e-3	5.67e-2	1.810
(52.5,0.175,1⁢0−5.975)	Radau		0.111	6590	310	tahun 1100	—	8.47e-5	1.115
	Radau	1⁢0−1.5	0,095	5342	277	tahun 1068	—	0,0079 tahun	1.432
	Bahasa Indonesia: ROM	2·1⁢0−4	0,057 tahun	tahun 1694	angka 0	angka 0	1.41e-3	3.08e-2	1.134
	Radau	1⁢0−3	0,074 tahun	4649	212	744	—	1.43e-5	0.467
	Radau	1⁢0−1.5	0,068 tahun	3654	197	712	—	0,0163	3.831
	Bahasa Indonesia: ROM	2·1⁢0−4	0,048 tahun	tahun 1454	angka 0	angka 0	3.45e-3	5.14e-2	5.976
	Radau	1⁢0−3	0,063 tahun	3895	183	666	—	3.73e-5	2.885
	Radau	1⁢0−1.5	0,033	tahun 1814	92	364	—	3.8838	464.3
	Bahasa Indonesia: ROM	2·1⁢0−4	0,049 tahun	tahun 1466	angka 0	angka 0	1.85e-3	6.27e-2	2.355
	Radau	1⁢0−3	0,062 tahun	3809	172	658	—	8.83e-5	7.598
	Radau	1⁢0−1.5	0,037 hari	Tahun 2021	100	392	—	2.6084	257.8
	Bahasa Indonesia: ROM	2·1⁢0−4	0,088	tahun 2690	angka 0	angka 0	2.17e-3	1.17e-2	1.366
	Radau	1⁢0−3	0.117	7148	319	tahun 1202	—	1.33e-5	1.100
	Radau	1⁢0−1.5	0,098	5433	292	tahun 1054	—	0,0039	1.888
	Bahasa Indonesia: ROM	2·1⁢0−4	0,059 tahun	tahun 1770	angka 0	angka 0	2.57e-3	2.28e-2	1.920
	Radau	1⁢0−3	0,077 tahun	4781	217	814	—	2.35e-5	1.102
	Radau	1⁢0−1.5	0,066 tahun	3635	196	712	—	0,0101	0,992

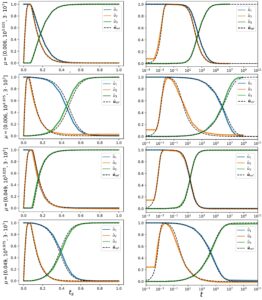
Catatan: Perbandingan biaya komputasi dan akurasi untuk penyelesai Radau dan ROM berbasis ODE neural pada set data pengujian. Lihat Bagian 4 untuk definisi metrik. Dalam huruf tebal, kesalahan terjadi saat solusinya tidak positif.

GAMBAR 8 — Perbandingan rasio kekakuan sistem OREGO dalam dinamika asli dan yang disederhanakan.

Kasus uji 2: OREGO, kondisi awal parametrik. Di sebelah kiri, dalam warna, prediksi ODE saraf di Di sebelah kanan, dalam warna, prediksi dipetakan ke waktu aslinya . Yang berwarna hitam adalah solusi referensi. Skala keadaan adalah logaritmik.

GAMBAR 10 — Kasus uji 3: ROBER. Di sebelah kiri, dalam warna, prediksi ODE saraf di Di sebelah kanan, dalam warna, prediksi dipetakan ke waktu aslinya Yang berwarna hitam adalah larutan referensi.

TABEL 3. Kasus uji 3: ROBER.

μ	Pemecah masalah	rtol (atol)	waktu [s]	# demam	#jev bahasa inggris	# aku	MSE ts	MSE
(0.006,1⁢03.025,3·1⁢07)	Bahasa Indonesia: ROM	2·1⁢0−4	0,008	230	angka 0	angka 0	1.21e-5	2.40e-4
	Radau	1⁢0−4⁢(1⁢0−7)	0,019	927	44	210	—	6.72e-6
	Radau	1⁢0−3⁢(1⁢0−6)	0,051 tahun	3055	132	798	—	9.58e11
(0.006,1⁢04.975,3·1⁢07)	Bahasa Indonesia: ROM	2·1⁢0−4	0,009	272	angka 0	angka 0	1.19e-3	1.11e-3
	Radau	1⁢0−4⁢(1⁢0−7)	0,021	tahun 1100	52	240	—	5.74e-6
	Radau	1⁢0−3⁢(1⁢0−6)	0,016	790	53	194	—	2.65e-5
(0.049,1⁢03.025,3·1⁢07)	Bahasa Indonesia: ROM	2·1⁢0−4	0,007 tahun	206	angka 0	angka 0	4.34e-4	4.97e-5
	Radau	1⁢0−4⁢(1⁢0−7)	0,021	tahun 1081	46	256	—	4.49e-6
	Radau	1⁢0−3⁢(1⁢0−6)	0,030	tahun 1787	73	406	—	1.9626
(0.049,1⁢04.975,3·1⁢07)	Bahasa Indonesia: ROM	2·1⁢0−4	0,009	260	angka 0	angka 0	4.46e-4	9.80e-4
	Radau	1⁢0−4⁢(1⁢0−7)	0,024	tahun 1121	55	248	—	3.35e-6
	Radau	1⁢0−3⁢(1⁢0−6)	0,014 tahun	795	50	198	—	1.50e-5

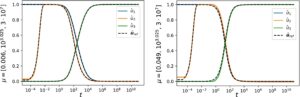
Catatan: Perbandingan biaya komputasi dan akurasi untuk penyelesai Radau dan ROM berbasis ODE neural pada set data pengujian. Lihat Bagian 4 untuk definisi metrik.

GAMBAR 11 — Kasus uji 3: ROBER. Prediksi model dengan toleransi integrasi tol dipetakan ke waktu aslinya Toleransi yang lebih kecil menghasilkan prediksi yang lebih akurat, lihat Gambar 10 .

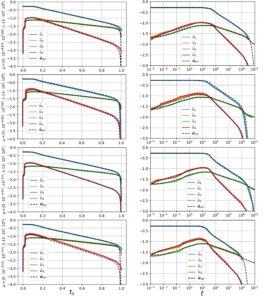
4.4 Kasus Uji 4: Masalah E5
Masalah E5 terdiri dari sistem kaku berikut dari 4 ODE nonlinier:

GAMBAR 12 — Kasus uji 4: E5. Di sebelah kiri, dalam warna, prediksi ODE saraf di Di sebelah kanan, dalam warna, prediksi dipetakan ke waktu aslinya . Yang berwarna hitam adalah solusi referensi. Skala keadaan adalah logaritmik.

TABEL 4. Kasus uji 4: E5.

μ	Pemecah masalah	rtol (atol)	waktu [s]	# demam	#jev bahasa inggris	# aku	MSE ts	MSE
(5·1⁢0−9.975,1⁢07.025,1.13e3,1⁢06)	Bahasa Indonesia: ROM	2·1⁢0−4	0,013	308	angka 0	angka 0	4.12e-2	5.06e-3
(5·1⁢0−9.975,1⁢07.025,1.13e3,1⁢06)	Radau	1⁢0−6⁢(1⁢0−20)	0,064 tahun	4119	93	416	—	8.36e-4
(5·1⁢0−9.025,1⁢07.025,1.13e3,1⁢06)	Bahasa Indonesia: ROM	2·1⁢0−4	0,015	344	angka 0	angka 0	4.97e-2	4.00e-3
(5·1⁢0−9.025,1⁢07.025,1.13e3,1⁢06)	Radau	1⁢0−6⁢(1⁢0−20)	0,065 tahun	4156	102	426	—	1.84e-2
(5·1⁢0−9.975,1⁢07.975,1.13e3,1⁢06)	Bahasa Indonesia: ROM	2·1⁢0−4	0,013	302	angka 0	angka 0	1.56e-2	4.80e-3
(5·1⁢0−9.975,1⁢07.975,1.13e3,1⁢06)	Radau	1⁢0−6⁢(1⁢0−20)	0,063 tahun	tahun 4003	103	430	—	9.87e-4
(5·1⁢0−9.025,1⁢07.975,1.13e3,1⁢06)	Bahasa Indonesia: ROM	2·1⁢0−4	0,011	260	angka 0	angka 0	6.48e-2	5.53e-3
(5·1⁢0−9.025,1⁢07.975,1.13e3,1⁢06)	Radau	1⁢0−6⁢(1⁢0−20)	0,068 tahun	4055	112	438	—	1.88e-2

Catatan: Perbandingan biaya komputasi dan akurasi untuk penyelesai Radau dan ROM berbasis ODE neural pada set data pengujian. Lihat Bagian 4 untuk definisi metrik.

TABEL 5. Laju reaksi referensi untuk model POLLU yang mendefinisikanμ(0).

Reaksi	r	μ(0)	Reaksi	r	μ(0)	Reaksi	r	μ(0)
1	μ1⁢u1	0.350e0	10	μ10⁢u11⁢u1	0.900e4	19	μ19⁢u16	0.444e12
2	μ2⁢u2⁢u4	0.266e2	11	μ11⁢u13	0,220e-1	20	μ20⁢u17⁢u6	0.124e4
3	μ3⁢u5⁢u2	0.120e5	12	μ12⁢u10⁢u2	0.120e5	21	μ21⁢u19	0.210e1
4	μ4⁢u7	0.860e-3	13	μ13⁢u14	0.188e1	22	μ22⁢u19	0.578e1
5	μ5⁢u7	0.820e-3	14	μ14⁢u1⁢u6	0.163e5	23	μ23⁢u1⁢u4	0.474e-1
6	μ6⁢u7⁢u6	0.150e5	15	μ15⁢u3	0.480e7	24	μ24⁢u19⁢u1	0.178e4
7	μ7⁢u9	0.130e-3	16	μ16⁢u4	0,350e-3	25	μ25⁢u20	0.312e1
8	μ8⁢u9⁢u6	0.240e5	17	μ17⁢u4	0,175e-1
9	aku9⁢kamu11⁢kamu2	0.165e5	18	aku18⁢kamu16	0.100e9

GAMBAR 13 — Kasus uji 5: POLLU. Di sebelah kiri, prediksi ODE saraf di Di sebelah kanan, prediksi dipetakan ke waktu aslinya . Dalam warna biru prediksi ODE sarafaku , dalam warna hitam larutan referensi.

TABEL 6. Kasus uji 5: POLLU.

μ	Pemecah masalah	tol	waktu [s]	# demam	#jev bahasa inggris	# aku	MSE ts	MSE
μi=0.525⁢μi(0),i=4,6,14	Bahasa Indonesia: ROM	1⁢0−4	0,006	194	angka 0	angka 0	6.89e-4	9.80e-4
	Radau	1⁢0−4	0,011	182	10	50	—	3.81e-3
	Radau	1⁢0−3	0,011	149	10	40	—	0.2077
μi=1.975⁢μi(0),i=4,6,14	Bahasa Indonesia: ROM	1⁢0−4	0,007 tahun	212	angka 0	angka 0	1.16e-3	1.69e-3
	Radau	1⁢0−4	0,017 tahun	268	14	70	—	9.03e-4
	Radau	1⁢0−3	0,014 tahun	203	12	54	—	4.63e-3

5 Kesimpulan
Dalam karya ini, kami telah mengembangkan metodologi baru untuk mengatasi beberapa jenis kekakuan dalam ODE neural. Pendekatan ini bergantung pada reparametrisasi waktu yang tepat dari sistem yang secara signifikan mengurangi kekakuan, sehingga memungkinkan penerapan pemecah eksplisit secara efisien pada ODE neural. Konstruksi reparametrisasi waktu bersifat umum dan sepenuhnya didorong oleh data, sehingga ideal untuk aplikasi pada ROM.

Dengan memanfaatkan kemampuan intrinsik ODE neural untuk menangani data waktu kontinu, kami menangkap dinamika sistem kaku secara efektif. Akurasi, ketahanan, dan efisiensi metodologi diuji dalam lima kasus uji tolok ukur terkenal dari literatur. Yaitu, ketika diterapkan pada sistem periodik, model tersebut digeneralisasi ke data yang jauh melampaui interval pelatihan waktu. Kami mengaitkan karakteristik ini terutama dengan sifat otonom ODE neural dan model reparametrisasi waktu. Ketika diterapkan pada persamaan kimia, model kami selalu mempertahankan kepositifan konsentrasi, bahkan ketika diterapkan pada masalah yang mengalami ketidakstabilan numerik. Selain itu, tradeoff kerja/presisi model kami sering terbukti sebanding atau menguntungkan ketika dihadapkan dengan penyelesai implisit Runge-Kutta mutakhir dari jenis Radau II A. Dalam beberapa kasus di mana hal ini tidak diamati, model kami memberikan alternatif yang lebih murah secara komputasi untuk solusi perkiraan sambil mempertahankan kepositifan konsentrasi, yang tidak mungkin dilakukan dengan penyelesai Radau untuk toleransi kecil.

Sebagai kesimpulan, penelitian kami menyoroti potensi menjanjikan dari ODE neural dalam menciptakan ROM yang efisien dan akurat untuk ODE kaku. Kekakuan yang dicirikan oleh nilai eigen yang cukup besar tetapi frekuensi yang sangat tinggi tetap menjadi tantangan bagi pendekatan kami, dan ini merupakan topik penelitian yang aktif. Penelitian di masa mendatang diarahkan untuk meningkatkan akurasi pemetaan waktu yang, hingga saat ini, merupakan hambatan akurasi utama ROM. Kami juga bertujuan untuk menguji kerangka kerja ini untuk menangani formulasi semi-diskrit dari PDE, dan sistem berdimensi lebih tinggi lainnya. Selain itu, teknik seperti distilasi model, pemangkasan jaringan, dan penyetelan hiperparameter yang lebih baik dapat lebih mengurangi biaya komputasi dari pendekatan kami.