Uji Asosiasi Kuat yang Memanfaatkan Interaksi Genetik yang Tidak Diketahui: Aplikasi pada Penyakit Paru Fibrosis Kistik

ABSTRAK
Untuk sifat kompleks seperti penyakit paru-paru pada Cystic Fibrosis (CF), interaksi Gen x Gen atau Gen x Lingkungan dapat memengaruhi tingkat keparahan penyakit tetapi ini sebagian besar masih belum diketahui. Interaksi genetik yang tidak diperhitungkan memperkenalkan pergeseran distribusional dalam sifat kuantitatif di seluruh kelompok genotipe. Uji lokasi dan skala gabungan, atau perbedaan distribusional penuh di seluruh kelompok genotipe dapat menjelaskan interaksi genetik yang tidak diketahui dan meningkatkan kekuatan untuk identifikasi gen dibandingkan dengan uji asosiasi konvensional. Di sini kami mengusulkan uji lokasi dan skala gabungan (JLS) baru, JLS berbasis regresi kuantil (qJLS), yang mengatasi keterbatasan sebelumnya. Secara khusus, qJLS bebas dari asumsi distribusional, dengan demikian berlaku untuk sifat non-Gaussian; sama kuatnya dengan uji JLS yang ada di bawah sifat Gaussian; dan efisien secara komputasi untuk studi asosiasi genom-lebar (GWAS). Studi simulasi kami, yang memodelkan interaksi genetik yang tidak diketahui, menunjukkan bahwa qJLS kuat terhadap distribusi kesalahan yang miring dan berekor tebal dan sama kuatnya dengan uji JLS lainnya dalam literatur di bawah normalitas. Tanpa adanya interaksi genetik yang tidak diketahui, qJLS menunjukkan peningkatan daya yang besar dengan sifat non-Gaussian dibandingkan uji asosiasi konvensional dan sedikit kurang kuat dalam keadaan normal. Kami menerapkan metode qJLS pada Studi Pengubah Gen CF Kanada (n = 1.997) dan mengidentifikasi varian signifikan di seluruh genom, rs9513900 pada kromosom 13, yang sebelumnya tidak dilaporkan berkontribusi terhadap penyakit paru CF. qJLS menyediakan alternatif yang kuat untuk uji asosiasi genetik konvensional, di mana interaksi dapat berkontribusi pada sifat kuantitatif.

1 Pendahuluan
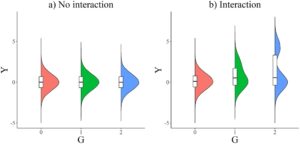
Uji asosiasi konvensional dalam studi asosiasi genom-lebar (GWAS) bertujuan untuk mendeteksi perubahan dalam mean kondisional untuk fenotipe kuantitatif di seluruh kelompok genotipik pada polimorfisme genetik. Untuk polimorfisme nukleotida tunggal (SNP) bi-allelik, Paré et al. ( 2010 ) menunjukkan bahwa interaksi yang tidak diketahui dari suatu gen dengan gen lain (G x G) atau dengan faktor lingkungan eksternal (G x E) dapat menginduksi perubahan dalam distribusi kondisional fenotipe di seluruh kelompok genotipik, yang bermanifestasi sebagai heterogenitas dalam varians kondisional. Oleh karena itu, interaksi genetik yang tidak diketahui dapat dideteksi melalui uji varians. Karena interaksi genetik umumnya tidak diketahui atau sulit diukur apriori, pendekatan tidak langsung ini, yang tidak memerlukan spesifikasi variabel yang berinteraksi dengan polimorfisme tertentu, adalah cara yang mudah untuk mendeteksi varian genetik yang berkontribusi yang mungkin dikaburkan oleh interaksi genetik yang tidak diketahui. Bahasa Indonesia: Ketika data pada variabel yang berinteraksi dikumpulkan, pemodelan interaksi G x G dan G x E merupakan alternatif yang lebih kuat (Paré et al. 2010 ), tetapi merupakan solusi yang tidak praktis karena banyaknya jumlah kombinasi interaksi dua arah G x G atau yang lebih tinggi, yang memperkenalkan pengujian hipotesis ganda dan beban komputasi. Ini dapat dihindari dengan uji varians tidak langsung. Akibatnya, ada minat baru dalam uji klasik untuk heterogenitas varians misalnya uji Bartlett (Bartlett 1937 ) dan uji Levene (Levene 1961 ). Uji-uji ini awalnya dikembangkan untuk memverifikasi asumsi yang mendasari dalam analisis varians. Baru-baru ini, kelas metode statistik baru menguji heterogenitas baik dalam mean kondisional dan varians secara bersama-sama, atau menguji perbedaan pada momen yang lebih tinggi atau dalam distribusi fenotipik di seluruh kelompok genotipik. Melalui studi simulasi, Soave et al. ( 2015 ) menunjukkan bahwa, dengan adanya interaksi genetik yang tidak diketahui, metode ini dapat lebih kuat daripada uji lokasi konvensional. Peningkatan kekuatan ini sangat penting untuk GWAS penyakit yang lebih langka seperti Cystic Fibrosis (CF) di mana jumlah total kasus yang tersedia untuk dipelajari terbatas.

Beberapa uji lokasi dan skala gabungan telah dikembangkan (Cao et al. 2014 ; Rönnegård dan Valdar 2011 ; Soave et al. 2015 ; Staley et al. 2021 ), dan mereka umumnya secara bersama-sama memodelkan lokasi dan skala distribusi fenotipik kondisional, dengan asumsi kesalahan didistribusikan secara normal. Perbedaan utama antara uji lokasi dan skala gabungan ini terletak pada estimasi parameter untuk varians kondisional dan proses iteratif untuk menyesuaikan model gabungan. Parameter untuk varians kondisional diestimasi baik berdasarkan residual kuadrat atau deviasi absolut, analog dengan uji Bartlett dan uji Brown-Forsythe (Brown dan Forsythe 1974 ), masing-masing, untuk prediktor diskrit. Dalam uji lokasi dan skala gabungan seperti uji lokasi-skala gabungan (Soave et al. 2015 ; Soave dan Sun 2017 ) dan uji skor lokasi-skala gabungan (Staley et al. 2021 ), parameter lokasi dan skala dipasang secara terpisah sedangkan, dalam yang lain seperti uji rasio kemungkinan (Cao et al. 2014 ) dan model linier umum ganda (Rönnegård dan Valdar 2011 ), proses iteratif berputar antara model lokasi dan model skala, yang memungkinkan estimasi gabungan parameter lokasi dan skala. Meskipun metode ini bekerja dengan baik dalam kenormalan, fenotip umumnya tidak normal. Transformasi normal terbalik berbasis peringkat merupakan teknik transformasi data yang populer dalam epidemiologi genetik, sebagai tindakan perbaikan untuk kesalahan non-normal (Rönnegård dan Valdar 2011 ; Soave et al. 2015 ; Beasley et al. 2009 ; McCaw et al. 2020 ). Namun, dampak penerapan transformasi ini pada kesalahan tipe I dan daya uji lokasi dan skala gabungan belum dipahami dengan baik. Kami memberikan tinjauan atas uji lokasi dan skala gabungan ini dan melakukan studi simulasi untuk menilai dampak penerapan transformasi normal terbalik berbasis peringkat pada kesalahan tipe I dan daya, dalam kondisi non-normal. Kami kemudian mengusulkan alternatif.

Kategori metode lain bertujuan untuk mendeteksi perubahan dalam mean, varians dan seterusnya (Hong et al. 2017 ) atau dalam kuantil tanpa syarat (Aschard et al. 2013 ) tanpa memerlukan asumsi distribusi apa pun. Meskipun metode ini kuat terhadap kesalahan non-normal, metode ini cenderung bernasib jauh lebih buruk daripada uji lokasi dan skala gabungan yang mengasumsikan kenormalan ketika distribusi istilah kesalahan mendekati distribusi normal (Soave et al. 2015 ). Selain itu, metode ini tidak dirancang untuk menggabungkan kovariat kontinu, yang dapat menyebabkan hasil palsu jika ini mengacaukan hubungan genetik. Terakhir, efisiensi komputasi membuat metode ini sulit untuk diterapkan secara genomik.

Regresi kuantil (Koenker dan Bassett 1978 ) menyediakan kerangka kerja alami dan kuat untuk mempelajari distribusi kondisional tanpa membuat asumsi distribusi apa pun. Aplikasinya dalam genomik telah berkembang dalam beberapa tahun terakhir (Briollais dan Durrieu 2014 ). Miao dkk. ( 2022 ) mengembangkan uji varians berdasarkan regresi kuantil untuk mendeteksi interaksi genetik yang tidak diketahui. Di sini, kami mengusulkan uji lokasi dan skala gabungan baru berdasarkan regresi kuantil yang tidak memerlukan asumsi kenormalan. Metode kami kuat terhadap kesalahan non-normal dan efisien secara komputasi, sementara kekuatannya di bawah normalitas sebanding dengan uji lokasi dan skala gabungan lainnya yang mengasumsikan kenormalan. Kami membandingkan kinerja uji ini dengan uji baru kami dalam studi simulasi yang menyertakan distribusi kesalahan miring dan berekor tebal. Akhirnya, kami menerapkan metode kami dalam GWAS penyakit paru-paru pada warga Kanada dengan CF.

2 Metode
Untuk tujuan ilustrasi, kami mempertimbangkan skenario sederhana dengan satu variabel paparan biner yang berinteraksi dengan SNP bi-allelic. Hal ini dapat dengan mudah digeneralisasikan ke skenario dengan beberapa variabel paparan bertipe kontinu atau diskret, atau polimorfisme lainnya. Kami mencatat bahwa paparan tidak harus bersifat lingkungan (yaitu interaksi G x E) dan dapat melibatkan SNP lain (yaitu interaksi G x G). Kami berasumsi bahwa variabel interaksi yang tidak diketahui tidak mengacaukan hubungan antara G dan respons, karena faktor pengganggu yang tidak diperhitungkan dapat menyebabkan temuan yang salah.

2.1 Notasi dan Model Interaksi Genetik

GAMBAR 1 — Ilustrasi efek variabel biner berinteraksi dengan varian bi-allelik pada fenotipe Gaussian :data disimulasikan berdasarkan Model 1 tanpa kovariat , memperbaiki efek utama Dan dengan ukuran sampel 1.000.000. dihasilkan dari variabel acak Bernoulli dengan probabilitas keberhasilan Dan dihasilkan berdasarkan frekuensi alel minor Pada (a), efek interaksi ditetapkan sebesar dan pada (b), efek interaksi ditetapkan sebesar .

2.2 Uji Lokasi dan Skala Gabungan dan Transformasi Normal Terbalik Berbasis Peringkat
Kami menyediakan tinjauan dari empat uji lokasi dan skala gabungan: uji rasio kemungkinan (likelihood ratio test/LRT) (Cao et al. 2014 ); model linear umum ganda (double generalized linear model/DGLM) (Rönnegård dan Valdar 2011 ); uji skala lokasi gabungan (JLS) (Soave et al. 2015 ); dan uji skor skala lokasi gabungan (JLSS) (Staley et al. 2021 ), di Bagian 3 Informasi Pendukung . Ini berbeda secara umum dari estimasi parameter skala, proses iteratif untuk menyesuaikan model gabungan dan kemampuan untuk memperhitungkan korelasi antara estimasi parameter lokasi dan skala. Uji skala dan lokasi gabungan ini memerlukan kenormalan istilah kesalahan. Ketika asumsi ini dilanggar, tindakan perbaikan yang umum adalah dengan mentransformasikan data. Transformasi normal terbalik (inverse normal transformation/INT) berbasis peringkat adalah teknik transformasi data yang populer dalam epidemiologi genetik, yang memetakan satu variabel ke variabel lain yang sepenuhnya normal. Ide transformasi data ini adalah untuk memperkirakan kuantil empiris dari variabel yang diminati melalui peringkat fraksionalnya dan menerapkan fungsi kuantil dari variabel acak normal. INT didefinisikan sebagai berikut:

Kami mencatat bahwa tingkat dampak INT pada kesalahan tipe I dan daya tidak dipahami dengan baik. Secara khusus, INT adalah transformasi nonlinier yang mengubah skala fenotipik, dan, sebagai konsekuensinya, kinerja uji skala diperkirakan akan terpengaruh oleh INT. Kami melakukan studi simulasi ekstensif untuk menyelidiki efek INT pada lokasi gabungan dan uji skala. Hasilnya menunjukkan bahwa penerapan I-INT2 mengarah pada kesalahan tipe I yang terkontrol dengan baik dan dapat meningkatkan daya di bawah non-normalitas. Rinciannya disediakan di Bagian 4 Informasi Pendukung . Namun, kami tidak yakin seberapa generalisasi hasil ini di luar skenario simulasi spesifik yang diselidiki. Dengan demikian, di bagian berikutnya, kami mengusulkan pendekatan baru yang kuat di mana kesalahan tipe I tidak bergantung pada asumsi distribusi sebelumnya dan sama kuatnya dengan uji lokasi dan skala lainnya di bawah normalitas. Kami menggunakan regresi kuantil sebagai kerangka uji, oleh karena itu, kami menyebut uji ini sebagai uji skala lokasi gabungan (qJLS) berbasis regresi kuantil.

Kami mencatat bahwa terdapat pengujian nonparametrik dan semiparametrik yang tangguh, dengan kesalahan tipe I tidak terpengaruh oleh distribusi kesalahan nonnormal. Akan tetapi, ketika distribusi kesalahan cukup dekat dengan distribusi normal, hal ini menunjukkan defisit daya dibandingkan dengan pengujian lokasi gabungan dan skala. Selain itu, metode ini tidak efisien secara komputasi dan tidak dapat menyesuaikan kovariat kontinu, yang mungkin merupakan faktor pengganggu seperti komponen utama untuk keturunan genetik.

2.5 Uji Skala Lokasi Gabungan Berbasis Regresi Kuantil (qJLS)
Perhatikan model regresi kuantil linier berikut:

Kami mencatat bahwa distribusi asimtotik dari statistik uji di bawah hipotesis nol tidak mengandung parameter apa pun dari distribusi galat. Oleh karena itu, galat tipe I tidak bergantung pada distribusi galat. Di sisi lain, fungsi skor dipilih berdasarkan optimalitas uji di bawah distribusi normal. Dengan kata lain, di bawah galat non-normal, galat tipe I dari uji qJLS masih terkontrol dengan baik, tetapi daya uji terpengaruh karena pilihan fungsi skor kami. Sebagai perbandingan, uji lokasi dan skala gabungan lainnya yang ditinjau dalam Bagian 3 Informasi Pendukung mengasumsikan kenormalan tetapi menunjukkan galat tipe I yang meningkat ketika distribusi galat menyimpang dari normalitas (Bagian 4 Informasi Pendukung ). Meskipun I-INT2 menunjukkan kontrol galat tipe I dan/atau peningkatan daya statistik, sifat statistiknya belum didefinisikan sebelumnya karena studi simulasi hanya mencakup sejumlah skenario terbatas. Sebaliknya, qJLS menjamin galat tipe I yang terkontrol dengan baik terlepas dari distribusi galat, keuntungan utama dibandingkan uji lokasi dan skala gabungan lainnya. Paket perangkat lunak qJLS tersedia untuk umum di Strug Lab, bersama dengan kode simulasi ( https://github.com/strug-hub/qJLS ).

2.6 Studi Simulasi
Kami mencatat bahwa sebagian besar studi simulasi dalam literatur menggunakan model heteroskedastik linear sebagai mekanisme pembangkitan data, yang hanya dapat menghasilkan pergeseran lokasi dan/atau skala. Namun, pengaturan seperti itu terbatas karena interaksi genetik yang tidak diketahui dapat mengubah seluruh bentuk distribusi kondisional fenotipe, di luar lokasi atau skala. Di sini, kami menggunakan model interaksi genetik (Model 1) seperti yang dijelaskan dalam Paré et al. Kami memperluas pengaturan simulasi oleh Aschard et al. ( 2013 ) untuk menyertakan galat non-normal, efek interaksi khusus kuantil, dan heterogenitas latar belakang yang tidak diketahui. Terakhir, kami menggunakan model lokasi dan skala linear untuk menghasilkan pergeseran lokasi atau skala murni tanpa interaksi genetik apa pun, ideal untuk pengujian lokasi konvensional dan pengujian skala, dan untuk mengevaluasi hilangnya daya dengan menggunakan uji lokasi dan skala gabungan dibandingkan dengan pengujian konvensional ini.

2.7 Daya
2.7.1 Interaksi Tunggal yang Tidak Diketahui
Berikut ini adalah model pembangkitan data:

GAMBAR 2 — Fungsi kepadatan dari istilah kesalahan untuk model simulasi: variabel acak yang dipilih termasuk normal standar (berwarna hijau), (berwarna biru) dan distribusi empiris dari SNP teratas yang residual di Bagian 4 (berwarna merah).

2.10 Perbandingan Metode
Dengan menggunakan simulasi, kami membandingkan kinerja uji lokasi gabungan dan skala (diulas dalam Bagian 3 Informasi Pendukung ) dengan uji qJLS. Ini termasuk model linear umum ganda (DGLM), uji skala lokasi gabungan (JLS) dan uji skor skala lokasi gabungan (JLS-Score). Kami mencatat bahwa uji DGLM, JLS dan JLS-Score memerlukan kenormalan istilah galat. Karena interaksi yang tidak diketahui mengubah bentuk distribusi, distribusi residual yang dihasilkan akan menunjukkan penyimpangan dari kenormalan berdasarkan plot QQ normal atau melalui uji statistik, bahkan jika istilah galat dalam Model 3 mengikuti distribusi normal. Atas dasar ini, kami menerapkan I-INT2 sebagai ukuran perbaikan untuk semua distribusi galat, termasuk distribusi normal karena studi simulasi kami di Bagian 4 Informasi Pendukung menunjukkan bahwa I-INT2 menghilangkan inflasi galat tipe I dengan distribusi galat yang miring atau berekor tebal dan varian lainnya, D-INT dan INT tidak langsung yang disesuaikan tunggal (I-INT1), masih mengakibatkan galat tipe I yang meningkat atau ketidakstabilan numerik dalam beberapa skenario. Oleh karena itu, kami menerapkan I-INT2 sebagai fungsi transformasi untuk pengujian DGLM dan JLS. Hasil simulasi awal kami menunjukkan bahwa pengujian JLS-Score tetap kuat dalam semua skenario simulasi yang kami pertimbangkan (Tabel S12 dalam Informasi Pendukung ). Namun, daya berkurang secara signifikan tanpa transformasi data apa pun di bawah hipotesis alternatif dalam skenario di mana istilah galat menyimpang jauh dari normalitas. Atas dasar ini, kami menerapkan INT untuk pengujian JLS-Score tetapi juga mempertimbangkan kasus tersebut tanpa transformasi data apa pun. Kami memilih I-INT2, semata-mata untuk tujuan perbandingan. Kami mencatat bahwa daya uji JLS-Score bervariasi dengan jenis INT, distribusi kesalahan dan jenis pergeseran distribusi dalam studi simulasi kami di Bagian 4 Informasi Pendukung dan tidak ada INT tunggal yang menghasilkan daya tertinggi. Kami tidak menerapkan fungsi transformasi apa pun untuk qJLS karena distribusi asimtotik statistik ujinya di bawah hipotesis nol tidak bergantung pada distribusi kesalahan di bawah hipotesis nol dan, oleh karena itu, kesalahan tipe I terkontrol dengan baik terlepas dari distribusi kesalahan. Untuk studi simulasi dengan Model 8a dan Model 8b yang didasarkan pada pergeseran lokasi murni dan pergeseran skala murni tanpa interaksi apa pun, kami tidak menerapkan transformasi apa pun saat kesalahannya normal karena kenormalan sebenarnya berlaku dalam skenario ini. Saat kesalahannya tidak normal, kami menerapkan INT langsung (D-INT) ke uji lokasi dan skala konvensional, karena ini umumnya digunakan dalam GWAS, dan I-INT2 untuk uji lokasi dan skala gabungan kecuali uji qJLS.

3 Hasil
3.1 Kesalahan Tipe I
Tabel 1 menampilkan kesalahan empiris tipe I, berbagai tingkat nominal dan distribusi kesalahan pada Model 6 dengan frekuensi alel minor 0,3 dan ukuran sampel
.

Tabel 1. Kesalahan empiris tipe I pada Model 6 yang memvariasikan distribusi kesalahan.

Distribusi Kesalahan	Nilai p nominal	Tidak ada transformasi				Saya-INT2
Distribusi Kesalahan	Nilai p nominal	DGLM	JLS	Skor JLS	qJLS	DGLM	JLS	Skor JLS
Normal	5×1⁢0−2	0,050225	0,049610	0,049605 pukul 12.00	0,049219	0,048864 tahun	0,049365	0,049581
	5×1⁢0−3	0,005031	0,004939	0,004921	0,004848	0,004747	0,004880	0,004916
	5×1⁢0−4	0,000506	0,000477	0,000480	0,000478	0,000461	0,000472	0,000480
	5×1⁢0−5	0,000063	0,000061	0,000056	0,000051	0,000053	0,000054	0,000056
χ2	5×1⁢0−2	0.204755	0,079244 tahun	0,049834	0,049380	0,048960	0,049550	0,049751
	5×1⁢0−3	0,084472 tahun	0,018055	0,004860	0,004745	0,004667	0,004844	0,004797
	5×1⁢0−4	0,037523	0,004398	0,000473	0,000504	0,000482	0,000483	0,000491
	5×1⁢0−5	0,017276	0,001057	0,000048	0,000055	0,000048	0,000052	0,000055
Data Empiris	5×1⁢0−2	0,034136	0,058374 tahun	0,050120	0,049429	0,048979	0,049795	0,049976
	5×1⁢0−3	0,003579	0,008962	0,005043	0,004904	0,004812	0,004933	0,004993
	5×1⁢0−4	0,000412	0,001525	0,000507	0,000494	0,000472	0,000496	0,000506
	5×1⁢0−5	0,000051	0,000263	0,000050	0,000047	0,000040	0,000050	0,000044

Catatan: Ukuran sampel dan frekuensi alel minor (MAF) ditetapkan pada 2000 dan 0,3, berturut-turut. Empat pengujian termasuk model linear umum ganda (DGLM), pengujian skala lokasi gabungan (JLS), pengujian skor skala lokasi gabungan (JLS-Score) dan pengujian skala lokasi gabungan berbasis regresi kuantil (qJLS) digunakan. Untuk tiga pengujian pertama, kami tidak menerapkan transformasi atau transformasi normal terbalik berbasis peringkat yang disesuaikan ganda tidak langsung (I-INT2) pada data. Kesalahan tipe I diperkirakan berdasarkan 1.000.000 replikasi.

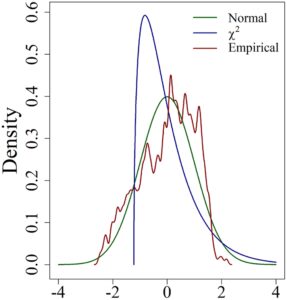
Berdasarkan distribusi normal standar, estimasi kesalahan tipe I untuk semua uji gabungan tanpa transformasi data apa pun mendekati setiap level nominal seperti yang diharapkan, dan distribusi nilai-p untuk semua uji gabungan tampak seragam dengan atau tanpa INT ( Informasi Pendukung: Gambar S3). Namun, tingkat kesalahan tipe I yang diestimasi untuk DGLM sedikit di atas semua level nominal. Berdasarkan distribusi normal standar, estimasi kesalahan tipe I untuk semua uji gabungan tanpa transformasi data apa pun mendekati setiap level nominal seperti yang diharapkan, dan distribusi nilai-p untuk semua uji gabungan tampak seragam dengan atau tanpa INT apa pun (Informasi Pendukung : Gambar S3). Namun, tingkat kesalahan tipe I yang diestimasikan untuk DGLM sedikit di atas semua level nominal. Berdasarkan distribusi normal standar, estimasi kesalahan tipe I untuk semua uji gabungan tanpa transformasi data apa pun mendekati setiap level nominal.
distribusi, inflasi terbukti untuk DGLM dengan kesalahan empiris tipe I yang besar, serta uji JLS yang menunjukkan inflasi yang relatif sedang. Untuk kedua metode, inflasi dikoreksi setelah menerapkan I-INT2. Histogram nilai-p dengan I-INT2 tampak seragam, yang selanjutnya mendukung koreksi dengan transformasi data ( Informasi Pendukung : Gambar S4). Untuk uji JLS-Score, transformasi data tidak diperlukan karena kesalahan empiris tipe I berada di bawah level nominal tanpa I-INT2. Di bawah distribusi data empiris, kesalahan empiris tipe I untuk DGLM jauh di bawah level nominal. Histogram nilai-p menunjukkan kemiringan ke kiri, yang menunjukkan bahwa metode tersebut terlalu konservatif untuk distribusi yang diberikan ( Informasi Pendukung : Gambar S5). Setelah menerapkan I-INT2, histogram nilai-p tampak seragam. Inflasi sedang dicatat untuk uji JLS tetapi dikoreksi setelah menerapkan I-INT2. Uji JLS-Score tetap kuat dalam skenario ini dengan kesalahan empiris tipe I di bawah level nominal. Dalam semua skenario, qJLS tidak menunjukkan bukti inflasi, seperti yang diharapkan.

Ketika ukuran sampel dikurangi, estimasi kesalahan tipe I meningkat untuk DGLM di bawah distribusi normal standar sedangkan metode lain tidak terpengaruh ( Informasi Pendukung : Tabel S1). Perilaku untuk DGLM ini konsisten dengan studi simulasi sebelumnya oleh Soave dan Sun ( 2017 ). Kesalahan tipe I empiris untuk DGLM sedikit di atas level nominal untuk semua ukuran sampel. Pada level nominal 0,05, estimasi kesalahan tipe I berada di atas level ini untuk semua ukuran sampel kecuali
Selain itu, ketika
, sekitar 0,011% dari replikasi tidak mencapai konvergensi numerik. Setelah menerapkan I-INT2, kesalahan tipe I empiris untuk DGLM turun di bawah level nominal. Transformasi tersebut menyelesaikan masalah optimasi dengan 100% dari replikasi mencapai konvergensi.
, DGLM menunjukkan kesalahan empiris tipe I yang besar dan peningkatan kegagalan dalam konvergensi numerik, mendekati 0,37% ketika
, yang diselesaikan dengan menerapkan I-INT2 ( Informasi Pendukung : Tabel S2). Inflasi moderat dicatat untuk uji JLS, yang dikoreksi setelah menerapkan I-INT2. Hasil untuk distribusi data empiris mengikuti pola yang diamati ketika
( Informasi Pendukung : Tabel S3). Kesalahan empiris tipe I untuk tes JLS-Score dan qJLS tidak menunjukkan tanda-tanda inflasi dengan perubahan ukuran sampel.

Pengurangan frekuensi alel minor mempengaruhi kesalahan tipe I empiris untuk semua metode kecuali uji JLS di bawah distribusi normal standar ( Informasi Pendukung : Tabel S4). Untuk DGLM, estimasi kesalahan tipe I sedikit di atas tingkat nominal ketika
Untuk uji JLS-Score dan qJLS, ketika frekuensi alel minor menurun, inflasi meningkat di bagian ekor distribusi nol, meskipun pada tingkat nominal 0,05 tidak ada inflasi yang diamati. Dalam semua kasus, penerapan I-INT2 tidak mengoreksi inflasi. Tren serupa diamati di bawah
dan distribusi data empiris ( Informasi Pendukung : Tabel S5 dan Tabel S6, masing-masing). Ketika frekuensi alel minor menurun, inflasi ringan diamati untuk DGLM dengan I-INT2 sedangkan inflasi ini terjadi di ekor distribusi nol untuk uji JLS-Score dengan I-INT2 dan uji qJLS. Tidak ada bukti inflasi untuk uji JLS dengan I-INT2 dalam skenario mana pun.

Tabel S7 ( Informasi Pendukung ) menampilkan efek dari heterogenitas latar belakang yang tidak diketahui yang memengaruhi lokasi dan skala distribusi fenotipik secara bersamaan pada kesalahan tipe I, yang menghasilkan ketergantungan antara estimator untuk parameter lokasi dan estimator untuk parameter skala. Karena uji DGLM dan JLS bergantung pada independensi estimator untuk parameter lokasi dan skala, kedua metode dipengaruhi oleh heterogenitas latar belakang. DGLM menunjukkan inflasi yang besar untuk semua distribusi kesalahan yang mencakup distribusi normal standar sedangkan inflasi sedang untuk uji JLS. Untuk kedua metode, inflasi dikoreksi setelah menerapkan I-INT2. Uji JLS-Score dan qJLS tetap kuat terhadap heterogenitas latar belakang yang tidak diketahui.

3.2 Daya
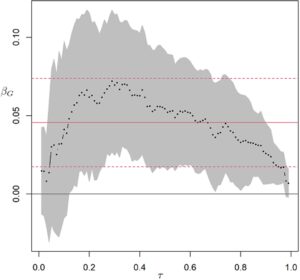
Gambar 3 menunjukkan perkiraan daya di bawah model interaksi tunggal yang tidak diketahui (Model 3) sebagai fungsi efek interaksi
berdasarkan frekuensi alel minor 0,3, ukuran sampel
dan 100.000 replikasi pada setiap nilai
. Berdasarkan distribusi normal standar, daya uji qJLS sedikit lebih besar daripada metode lain yang memerlukan I-INT2. Di antara ketiga metode yang memerlukan I-INT2 ini, tidak ada perbedaan daya yang terlihat. Berdasarkan
distribusi, uji qJLS menunjukkan daya terbesar ketika efek interaksi negatif, diikuti oleh DGLM. Ketika efek interaksi positif, uji JLS dan JLS-Score menunjukkan daya yang lebih besar daripada qJLS dan DGLM. Berdasarkan distribusi data empiris, uji qJLS adalah yang paling kuat untuk nilai negatif dan positif

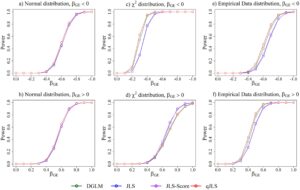
Gambar 4 menunjukkan daya yang diestimasikan berdasarkan model interaksi tak diketahui khusus kuantil (Model 4). Uji qJLS menunjukkan daya terbesar untuk semua distribusi galat. Menariknya, daya uji JLS dan JLS-Score kira-kira 0 untuk semua distribusi galat yang dipertimbangkan, yang menunjukkan bahwa uji JLS dan JLS-Score tidak dapat mendeteksi perubahan distribusi ini di bagian ekor..

Pada Gambar 5 , daya diestimasi untuk dua variabel yang berinteraksi, yang satu ditetapkan dengan efek lemah sebesar 0,2 dan efek interaksi yang lain divariasikan, berdasarkan Model 5. Untuk galat normal, daya yang diestimasi adalah yang terbesar untuk uji qJLS. Pola serupa muncul untuk
dan distribusi data empiris.

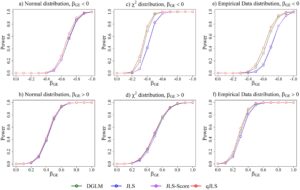
Gambar 6 menunjukkan estimasi daya untuk dua variabel yang berinteraksi dengan efek interaksi yang berlawanan, berdasarkan Model 5. Uji qJLS menunjukkan daya terbesar untuk semua distribusi kesalahan.
dan distribusi data empiris, perbedaan kekuatan antara uji qJLS dan tiga uji lainnya lebih jelas.

3.3 Perbandingan dengan Uji Asosiasi Konvensional
Gambar S1 ( Informasi Pendukung ) menunjukkan perbandingan daya antara regresi linier klasik dan uji lokasi dan skala gabungan di bawah model pergeseran lokasi murni tanpa interaksi apa pun (Model 8a), yang memvariasikan distribusi efek genetik dan galat utama. Dalam skenario dengan distribusi normal standar, regresi klasik diketahui menghasilkan penduga tak bias linier terbaik. Teori ini ditunjukkan dengan baik dalam Gambar S1 ( Informasi Pendukung ) di mana regresi linier adalah yang paling kuat, meskipun pengurangan daya untuk uji lokasi dan skala gabungan sedang. Perbedaan rata-rata atas semua ukuran efek yang dipertimbangkan adalah 3% dengan perbedaan maksimum 11%. Studi simulasi lebih lanjut menunjukkan bahwa uji qJLS memerlukan peningkatan sekitar 12% dalam ukuran sampel untuk mencapai daya yang sama dalam kondisi ini. Saat mempertimbangkan
, semua uji lokasi dan skala sambungan memperlihatkan peningkatan besar dalam daya jika dibandingkan dengan regresi klasik, yang dengan jelas menunjukkan manfaat dalam skenario ini.

Demikian pula, uji Levene umum untuk heterogenitas varians dibandingkan dengan uji lokasi gabungan dan skala di bawah model pergeseran skala murni (Model 8b), dengan memvariasikan efek varians utama
dan distribusi kesalahan ( Informasi Pendukung : Gambar S2). Anehnya, uji DGLM dan qJLS menunjukkan daya terbesar dengan peningkatan besar atas uji Levene umum di bawah distribusi normal standar. Perbedaan daya antara DGLM dan qJLS minimal. Uji JLS dan JLS-Score memiliki daya yang agak lebih rendah dibandingkan dengan uji Levene umum. Untuk distribusi kesalahan yang tersisa, qJLS menunjukkan perbedaan positif yang besar dibandingkan dengan pengujian yang tersisa. Tidak ada perbedaan daya untuk pengujian kecuali qJLS yang dapat dilihat dari Gambar S2 ( Informasi Pendukung ).

4 Aplikasi untuk Fibrosis Kistik
4.1 Motivasi
Fibrosis Kistik (CF) adalah penyakit resesif yang membatasi kehidupan yang disebabkan oleh varian hilangnya fungsi pada regulator konduktansi transmembran CF ( CFTR ). Individu dengan genotipe CFTR yang sama memiliki tingkat keparahan penyakit yang bervariasi di beberapa organ yang terkena CF termasuk paru-paru mereka, seperti variasi fungsi paru-paru yang dijelaskan sebagian oleh pengubah gen dan diasumsikan memiliki arsitektur genetik yang kompleks (Corvol et al. 2015 ). Mengidentifikasi varian genetik umum yang berkontribusi memerlukan ukuran sampel yang besar yang sulit untuk disusun untuk penyakit langka seperti CF. Uji statistik yang lebih kuat yang dapat memanfaatkan potensi interaksi yang tidak diketahui melalui heterogenitas varians, seperti qJLS yang kami terapkan di sini, dapat melemahkan tantangan ini.

4.2 Metode
4.2.1 Sampel Studi
Studi Pengubah Gen CF Kanada (CGMS) dirancang untuk merekrut sampel representatif dari populasi CF Kanada dengan tujuan untuk mengidentifikasi gen yang mengubah tingkat keparahan penyakit CF di seluruh organ yang terkena dan terutama di paru-paru (Taylor et al. 2006 ). Di sini kami menyelidiki penggunaan uji skala lokasi bersama untuk mengidentifikasi lokus yang mengubah tingkat keparahan penyakit paru-paru. Studi ini disetujui oleh Dewan Etika Penelitian Rumah Sakit untuk Anak Sakit dan persetujuan tertulis diperoleh dari setiap peserta.

Data klinis diperoleh melalui tinjauan grafik dan melalui Registri CF Kanada, yang menangkap tindak lanjut longitudinal populasi CF Kanada.

4.2.2 Fenotipe Paru
Kami menggunakan data spirometri longitudinal dalam 3 tahun terakhir sebelum tanggal pendaftaran untuk setiap peserta yang terdaftar dalam CGMS yang data genotipe genomiknya tersedia. Jika data fenotipe hilang sebelum tanggal pendaftaran, kami menggunakan rentang data 3 tahun terdekat setelah tanggal pendaftaran. Analisis dibatasi pada individu dengan setidaknya 2 atau lebih kunjungan setelah usia 6 tahun untuk pengukuran spirometri yang andal. Mengikuti konvensi untuk fungsi paru CF GWAS (Corvol et al. 2015 ), kami hanya menyertakan individu dengan dua varian CFTR parah yang terkait dengan insufisiensi pankreas (PI) (Corey et al. 1997 ) dan menghapus pengukuran setelah transplantasi, diagnosis B. Cepacia kronis , atau pengobatan dengan modulator CFTR . Kami menghitung fenotipe paru CF Saknorm (Taylor et al. 2011 ), yang merupakan persentil normal standar FEV1 yang disesuaikan dengan usia, jenis kelamin, tinggi badan, dan kelangsungan hidup spesifik kohort. Untuk menghasilkan persentil FEV1 yang disesuaikan dengan usia, jenis kelamin, dan tinggi badan, kami menggunakan persamaan referensi khusus CF oleh Kulich et al. ( 2005 ) yang berdasarkan pada US CF Foundation (CFF) Registry dari tahun 1999 hingga 2006 untuk kelompok yang terdaftar dalam CGMS sebelum tahun 2008 dan persamaan referensi khusus CF Kanada (Kim et al. 2018 ) yang berdasarkan pada data Canadian CF Registry dari tahun 2008 hingga 2014 untuk mereka yang terdaftar setelah tahun 2008. Untuk menghindari ekstrapolasi, kami mengeluarkan individu dengan tinggi badan di luar 5 cm dari rentang tinggi badan untuk persamaan referensi khusus CF. Kami kemudian menyesuaikan probabilitas kelangsungan hidup khusus kelompok untuk setiap persentil FEV1 dan menghitung rata-ratanya untuk setiap individu. Kami mencatat bahwa kami tidak menerapkan fungsi kuantil normal standar pada fenotipe ini seperti pada Taylor et al. ( 2011 ) karena metode statistik kami, qJLS, tidak memerlukan kenormalan. Untuk pengujian DGLM, JLS dan JLS-Score yang memerlukan normalitas, kami menerapkan I-INT2.

4.2.3 Data Genotipe Seluruh Genom
Genotyping dilakukan pada empat platform Illumina 610Quad, 660 W, Omni 2.5 dan Omni 5. Kontrol kualitas (QC) dan prosedur imputasi terperinci dijelaskan dalam Gong et al. ( 2019 ). Informasi posisi dan anotasi SNP didasarkan pada Genome Reference Consortium 37 (GRCh37). Kami menyertakan partisipan yang tidak terkait untuk memenuhi asumsi qJLS, dengan mengambil sampel secara acak satu individu dari setiap set individu terkait. Selain itu, dalam analisis komponen utama (Gogarten et al. 2019 ), observasi dalam 6 standar deviasi dari pusat klaster Afrika (AFR) atau Asia Timur (EAS) menggunakan data 1000 Genomes Project dikecualikan dari analisis.

4.2.4 Analisis Asosiasi
GWAS dilakukan dengan menggunakan uji qJLS. Sebagai perbandingan, kami menggunakan uji DGLM, JLS dan JLS-Score setelah menerapkan I-INT2. Kami menggunakan data dosis dengan asumsi efek aditif dan menyertakan jenis kelamin, jenis persamaan referensi yang digunakan untuk menghitung Saknorm, platform genotipe dan 9 komponen utama sebagai kovariat. Untuk memperhitungkan pengujian hipotesis ganda, kami menggunakan ambang batas signifikansi genomik
(Dudbridge dan Gusnanto 2008 ).

4.3 Hasil
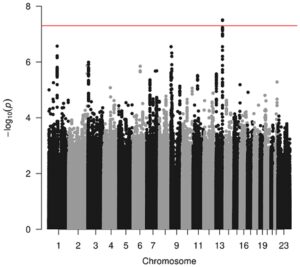
Setelah menerapkan kriteria inklusi-eksklusi di atas, total 1997 peserta dengan CF dimasukkan dalam analisis. Setelah QC standar dan imputasi (Panjwani et al. 2018 ; Gong et al. 2019 ), 5.533.051 varian dianalisis untuk mengetahui hubungannya dengan penyakit paru CF menggunakan Saknorm.

Satu lokus (nilai p minimal
pada rs9513900 pada chr13:102,090,156; MAF = 0,31), dijelaskan antara ITGBL1 (chr13:102,105,026-102,373,206) dan NALCN (chr13:101,706,128-102,068,859) secara signifikan dikaitkan dengan Saknorm menggunakan

GAMBAR 7 — Plot Manhattan untuk studi asosiasi genom-lebar penyakit paru CF dengan sampel 1997 individu yang tidak terkait di CGMS berdasarkan qJLS: Semua varian dengan MAF 1% disertakan dalam analisis. Garis horizontal padat berwarna merah sesuai dengan ambang batas signifikansi genom secara luas SNP teratas adalah varian rs9513900.

GAMBAR 8 — Perkiraan dampak varian rs9513900 pada fenotipe paru CF pada persentil yang berbeda : model regresi kuantil digunakan dengan data dosis yang mengasumsikan efek aditif. Prediktor meliputi jenis kelamin, jenis persamaan referensi khusus CF yang digunakan untuk menghitung fenotipe paru, platform genotipe, dan 9 komponen utama. Area abu-abu yang diarsir menunjukkan pita kepercayaan simultan menggunakan koreksi Bonferroni. Garis merah pekat adalah efek rata-rata, dengan garis merah putus-putus yang menunjukkan pita kepercayaan.

5 Diskusi
Dalam studi ini kami mengusulkan uji lokasi dan skala gabungan baru, qJLS, berdasarkan regresi kuantil dan membandingkan kinerjanya dengan pilihan uji lokasi dan skala gabungan dalam literatur. Manfaat utama uji qJLS adalah ketahanannya terhadap distribusi kesalahan yang mendasarinya sambil tetap menjadi yang paling kuat dalam kenormalan. Fitur ketahanan ini disebabkan oleh distribusi asimtotik dari statistik uji yang sepenuhnya bebas dari parameter untuk distribusi kesalahan, di bawah hipotesis nol. Sebaliknya, uji lokasi dan skala gabungan dalam literatur didasarkan pada asumsi kenormalan yang memerlukan transformasi, seperti transformasi normal terbalik berbasis peringkat, untuk kontrol laju kesalahan tipe I dan peningkatan daya. Meskipun studi simulasi kami memberikan beberapa dukungan untuk kontrol laju kesalahan tipe I dengan transformasi normal terbalik berbasis peringkat yang disesuaikan ganda tidak langsung, ini berada di bawah skenario tertentu dan generalisasi hasil memerlukan bukti teoritis yang saat ini kurang.

Dalam hal daya, kami sengaja merancang pengujian kami untuk mencapai keoptimalan dalam kondisi normal. Namun, ketika asumsi ini gagal, pengujian qJLS masih lebih kuat daripada metode lain dalam sebagian besar skenario simulasi yang dipertimbangkan. Dasar untuk kinerja ini terutama disebabkan oleh komponen skala pengujian. Kami mengamati bahwa komponen skala pengujian qJLS lebih kuat daripada komponen lokasi gabungan dan pengujian skala lainnya sementara daya untuk komponen lokasi tetap sama untuk semua pengujian yang dipertimbangkan. Perbedaan ini ditunjukkan dengan jelas ketika kami mempertimbangkan interaksi khusus ekor pada Gambar 4. Namun, daya pengujian adalah fungsi dari sifat pergeseran distribusi di bawah distribusi alternatif dan galat. Karena distribusi galat berbeda antara fenotipe dan interaksi genetik yang tidak diketahui dapat memengaruhi distribusi galat dengan cara yang berbeda, keoptimalan pengujian mungkin khusus skenario, yang membuatnya sulit untuk menentukan pengujian optimal apriori untuk data kehidupan nyata. Hal ini ditunjukkan pada Gambar 3 di mana qJLS kurang kuat daripada pengujian JLS dan JLS-Score untuk efek interaksi negatif di bawah standar
distribusi. Meskipun kami memilih fungsi-fungsi peringkat skor yang optimal untuk pergeseran lokasi dan skala dalam kenormalan, ada fungsi-fungsi peringkat skor alternatif yang optimal untuk jenis-jenis pergeseran distribusi dan distribusi galat lainnya (Koenker 2010 ). Kami melakukan studi simulasi tambahan berdasarkan Model 3, untuk bereksperimen dengan fungsi-fungsi peringkat skor alternatif yang didefinisikan dalam Koenker ( 2010 ) seperti fungsi Lehmann, Wilcoxon dan Wilcoxon yang dipangkas yang mencakup kuantil atas di atas median atau kuantil bawah di bawah median, dan membandingkannya dengan uji qJLS (Gambar S6 dalam Informasi Pendukung ). Uji qJLS bekerja dengan baik secara keseluruhan tetapi, dalam beberapa skenario, kekuatannya lebih rendah daripada beberapa uji peringkat skor alternatif. Akan tetapi, kinerja uji peringkat skor alternatif ini ekstrem, dengan kekuatan mendekati 0 dalam beberapa skenario. Berdasarkan temuan-temuan ini, kami menyimpulkan bahwa qJLS akan menawarkan kinerja yang baik pada rentang data yang dapat diamati.

Kami juga mengeksplorasi manfaat penggunaan qJLS dibandingkan uji lokasi atau skala konvensional. Manfaat ini ditunjukkan dengan jelas dengan adanya interaksi genetik yang tidak diketahui. Karena interaksi genetik yang tidak diketahui menggeser distribusi fenotipik bersyarat, qJLS memanfaatkan kekuatan yang lebih unggul dengan memanfaatkan pergeseran lokasi dan skala, daripada setiap pergeseran secara individual seperti dalam pengujian konvensional. Ketika kami mempertimbangkan pergeseran lokasi atau skala murni tanpa interaksi genetik yang tidak diketahui, qJLS masih lebih kuat daripada uji lokasi atau skala individual kecuali ketika kami mempertimbangkan model pergeseran lokasi murni dengan normalitas. Ini adalah skenario ideal untuk regresi linier, namun, perbedaan daya tampak sedang. Berdasarkan data simulasi dengan Model 8a, pengujian qJLS memerlukan peningkatan sekitar 12% dalam ukuran sampel untuk mencapai daya yang sama dalam kondisi optimal ini untuk regresi linier. Mengingat manfaat keseluruhan, kami merekomendasikan penggunaan qJLS dibandingkan pengujian konvensional.

Manfaat qJLS diilustrasikan dengan baik oleh GWAS dan hasil terkaitnya. Pertama, kami mencatat bahwa, dengan 5.533.051 varian, pengujian qJLS menunjukkan waktu komputasi tercepat. Hal ini diharapkan karena pengujian ini menghitung skor peringkat yang banyak menggunakan komputasi hanya sekali di bawah hipotesis nol sementara iterasi yang tersisa untuk masing-masing dari 5.533.051 varian terdiri dari perkalian dan penjumlahan sederhana. Kedua, pengujian qJLS kami mendeteksi varian kandidat meskipun melakukan pergeseran lokasi tanpa pergeseran signifikan dalam skala fenotipik; nilai p-nya
hanya sedikit lebih tinggi dibandingkan dengan hasil regresi linier
Pengurangan ukuran sampel yang diperlukan untuk mencapai daya 80% dan 90% dibandingkan dengan regresi linier masing-masing adalah sekitar 7,5% dan 3,7%, berdasarkan teknik bootstrapping dengan pengambilan sampel independen dan signifikansi genom secara luas.
. Pemeriksaan lokus genomik yang teridentifikasi menunjukkan bahwa SNP adalah eQTL untuk NALCN , protein nonselektif saluran kebocoran natrium. NALCN mengatur pergerakan sel epitel ke jaringan yang jauh, termasuk epitel paru-paru (Rahrmann et al. 2022 ). Temuan sebelumnya (Corvol et al. 2015 ; Soave dan Sun 2017 ; Gong et al. 2019 ; Panjwani et al. 2018 ) telah menunjukkan bahwa pengubah penyakit paru CF memengaruhi tingkat keparahan melalui perannya dalam variasi ekspresi gen, memberikan dukungan tambahan untuk lokus, meskipun replikasi dalam sampel independen diperlukan untuk menetapkan gen ini sebagai pengubah. Kami juga memeriksa efek khusus persentil yang semuanya positif, yang menunjukkan varian tersebut memberikan efek perlindungan di semua persentil fenotipe paru-paru. Tetapi efek ini tidak seragam di seluruh persentil dan tampaknya kuadratik. Pada kedua ekstrem fenotipe, sekitar 1% dan 99%, efeknya hampir nol dan mencapai efek maksimumnya pada persentil ke-29. Efek diferensial ini menunjukkan adanya interaksi potensial, meskipun tidak ada pergeseran skala yang terdeteksi. Penjelasan yang mungkin untuk kegagalan mendeteksi pergeseran skala adalah bahwa ukuran sampel saat ini tidak cukup untuk mendeteksi besarnya pergeseran skala yang diberikan.

Studi kami menyediakan tinjauan dan perbandingan kinerja di seluruh pilihan lokasi gabungan dan uji skala yang bergantung pada kenormalan, berdasarkan studi simulasi. Temuan kami menunjukkan bahwa DGLM yang menggunakan residual kuadrat untuk model skala lebih sensitif terhadap penyimpangan dari kenormalan daripada JLS dan JLS-Score yang menggunakan deviasi absolut yang kuat, tanpa transformasi data apa pun. Sebagai contoh yang jelas, DGLM menampilkan kesalahan tipe I yang meningkat bahkan dengan distribusi logistik yang sering tidak dapat dibedakan dari distribusi normal menggunakan plot QQ atau uji statistik untuk kenormalan seperti uji Kolmogorov–Smirnov. DGLM diketahui mengalami ketidakstabilan numerik dengan frekuensi alel minor yang rendah (Dumitrascu et al. 2019 ). Dalam pengalaman kami, ketidakstabilan ini meningkat dengan faktor-faktor tambahan seperti distribusi kesalahan yang miring dan berekor tebal, ukuran sampel yang rendah, dan sejumlah besar prediktor. Kami menunjukkan bahwa penerapan transformasi normal terbalik berbasis peringkat yang disesuaikan ganda tidak langsung memperbaiki inflasi galat tipe I dan ketidakstabilan numerik, untuk skenario yang dipertimbangkan. Uji JLS tanpa transformasi data apa pun lebih kuat terhadap kesalahan spesifikasi distribusi tetapi menunjukkan inflasi sedang dalam tingkat galat tipe I dengan distribusi miring atau berekor tebal. Inflasi ini dikoreksi dengan menerapkan I-INT2 untuk model homoskedastik tetapi, dengan heterogenitas varians, uji JLS masih menunjukkan sedikit inflasi dalam galat tipe I, mungkin karena estimasi independen dari parameter lokasi dan skala. Kami mencatat bahwa uji JLS-Score yang memperhitungkan korelasi antara parameter lokasi yang diestimasi dan parameter skala tetap kuat dalam skenario simulasi yang diselidiki. Meskipun galat tipe I tetap terkontrol dengan baik, itu adalah daya yang menderita ketika asumsi normalitas dilanggar. Menerapkan I-INT2 menghasilkan peningkatan daya yang besar tetapi sifat teoritis dengan transformasi data tidak diketahui dan masih harus diselidiki.

Kami mencatat bahwa keterbatasan qJLS adalah ia dirancang untuk pengamatan independen dan tidak dapat mengakomodasi individu terkait atau pengamatan berulang. Strategi untuk memenuhi persyaratan ini adalah dengan mempertahankan satu individu per kelompok individu terkait, yang mengakibatkan pengurangan ukuran sampel yang tidak diinginkan. Penelitian mendatang akan memperluas qJLS untuk memperhitungkan korelasi dalam data.